
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
So, astronomers have many different types of telescope to collect the light of stars. The two most basic pieces of information about a star that we can gather are
We've already discussed coordinate systems to describe the position of a star; today, let's look at the way that astronomers describe the brightness of a star. It's not quite as straightforward as you might imagine...
Before we get to stars, let's talk about the way people describe the properties of ordinary objects in the everyday world. For example, the mass of different animals.
Suppose we pick three similar animals: a dog, a human, and a cow.
Q: Which animal is the most massive?
Q: Roughly how many times more massive
is a human than a dog?
Note two properties of the "mass" system of measurement:
These seem so obvious that you might wonder why I'm bothering to mention them. Well, as you will see, these properties are NOT shared by the magnitude system.
People in all corners of the world have looked up at the stars (after all, without television, what else could they do at night?). We have detailed records from several cultures in the Middle East; in some, priests spent years studying the motions of the stars and planets, often trying to predict events in the future. Their motives may have been ill-founded, but in some cases, they did make very good measurements of what they could see.
Hipparchus of Rhodes compiled a catalog of about 850 stars. He described the brightness of each star by placing it in one of six categories, which one could call "brighest, bright, not so bright, not so faint, faint, faintest." Later scientists used the word "magnitude" to describe these categories.
mag-ni-tude n.
1. a. Greatness of rank or position: "such duties as were expected
of a landowner of his magnitude" (Anthony Powell).
b. Greatness in size or extent: The magnitude of the flood
was impossible to comprehend.
c. Greatness in significance or influence:
was shocked by the magnitude of the crisis.
From the American Heritage Dictionary of the English Language,
Fourth Edition Copyright 2000 by Houghton Mifflin Company.
The brightest stars were assigned to "the first magnitude", just as we would call the best movies or restaurants "first rate." The next-brightest stars were called "second magnitude", and so on down to the faintest stars visible to the unaided eye, which were called "sixth magnitude."
This is the origin of the peculiar convention that
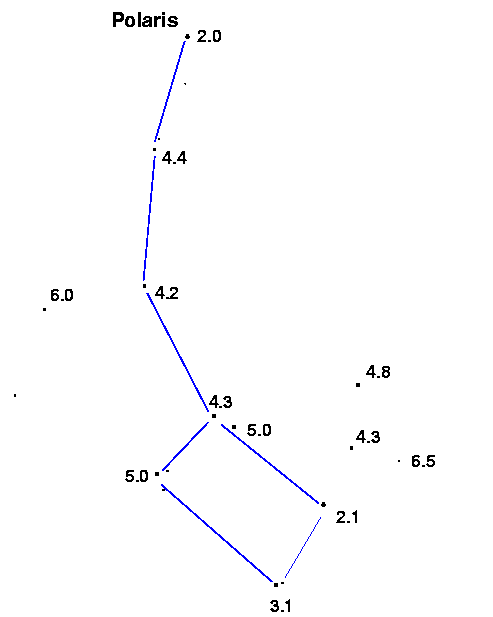
If you want to test yourself sometime, go outside on a clear night and look north. Find the Big Dipper, and use its "Pointers" to locate the Little Dipper.

Polaris, the North Star, is the brightest star in the Little Dipper; it shines at magnitude 2 at the tip of the handle. The other stars in the Little Dipper are much fainter -- how faint can you see?
If you see two stars, side by side, and you estimate that the one on the left is about "twice as bright" as the one of the right, does that mean that the star on the left really causes twice as many photons to strike your eye each second? No! Your eyes, like your ears, have evolved to handle a very wide range of environmental stimuli. These human (and animal) senses apparently work on a logarithmic scale.
What's a logarithm? It is a way of re-labelling numbers so that their values are compressed.
original value logarithm base 10
--------------------------------------------
1 0
10 1
100 2
1,000 3
10,000 4
100,000 5
1,000,000 6
--------------------------------------------
Logarithms can save a lot of space and breath. Instead of having to write (or say) 5,248,000,000 = "five billion, two-hundred and forty-eight million," you can simply write (or say) 9.72 = "nine point seven two."
Why do human senses work this way? In the real world, there can be a huge range between, say, the quietest important sound and the loudest important sound.
The sound of the gunshot is about 1014 = 100 trillion times higher in intensity than the sound of a whisper. But humans need to be able to hear both. Audio scientists invented the decibel system to compress this huge range of intensities into a more manageable range. On that scale, a whisper is about 20 decibels, and a gunshot about 160 decibels. Much more convenient ....
If you create two different sounds in a lab, and ask people to turn a knob until one sound is "about twice as loud as the other", you will find that
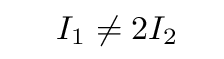
Instead, the relationship will be something closer to

In other words, human perception turns a true ratio of 10 in intensity into a smaller factor. Something similar happens when people try to describe the brightness of lights they see with their eyes.
In the nineteenth century, astronomers devised a number of tools which allowed them for the first time to make accurate, quantitative measurements of stellar brightness. They discovered two properties of the traditional magnitude classifications:
An astronomer named N. R. Pogson came up with a system which would roughly preserve the ancient magnitude values, while allowing modern scientists to extend it to more precise measurements. He proposed that the magnitude system be defined as follows: given two stars with intensity of brightness I1, I2, define a magnitude difference which is based on their ratio of intensities:
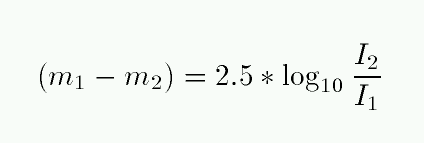
So, for example,
intensity intensity ratio magnitude difference
I(1) I(2) I(1)/I(2) (m1 - m2)
---------------------------------------------------------------
1 0.01 0.01 +5.00
1 0.1 0.1 +2.50
1 0.5 0.5 +0.75
1 1 1 0.0
1 2 2 -0.75
1 10 10 -2.50
1 100 100 -5.00
---------------------------------------------------------------
Q: Star A appears 50 times brighter than star B.
The magnitude of star A is 1.4. What is the
magnitude of star B?
Note again the counterintuitive sign of magnitude differences: the brighter star has a smaller magnitude.
Note also that this definition says nothing about the zero-point of a magnitude: it provides only the DIFFERENCE between two stars. Exactly where to set the zero-point of the magnitude scale is a matter of some debate, and eventually comes down to an arbitrary choice. We'll deal with it later.
If one is given the magnitudes of two stars, one can easily calculate the ratio of their intensities; just invert the above equation to find
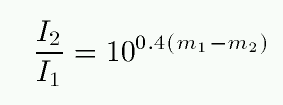
Q: One of the stars in the handle of the Big Dipper is
really a pair of stars, Alcor and Mizar, just far enough
apart for people with good eyes to distinguish.
Given magnitudes of 4.00 for Alcor and 2.06 for Mizar,
how many times brighter is Mizar than Alcor?
Note that even a relatively small difference in magnitudes can mean a very large ratio of brightness. For example, Sirius, the brightest star in the sky, has a magnitude of about -1.4. If you look at a chart of its constellation (Canis Major), it is drawn as the biggest circle:

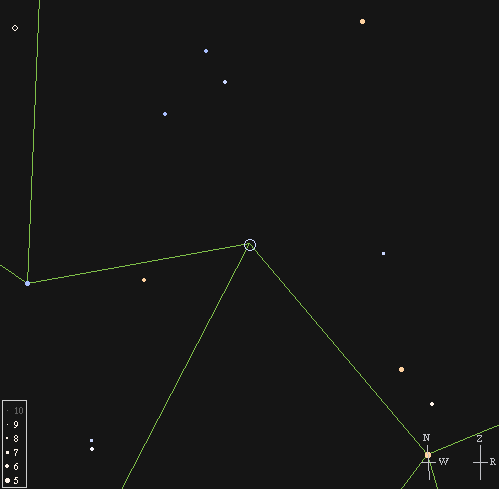
The stars in the little triangle to the upper-left of Sirius are about magnitude 5.
Q: How many times brighter is Sirius (mag -1.4)
than a star of magnitude 5?
Wow! That's much brighter, as you will see at once if you look at a photograph of the area:

Q: The average diameter of the dark-adapted pupil in a human eye
is about 6 millimeters;
the average person can see a star of magnitude 6 on a clear,
dark night.
If the same person were to look through typical 7x35 binoculars,
how faint a star might he be able to detect?
There are drawbacks to the magnitude system. One of the big ones is the work one must do when trying to figure out the result of adding or subtracting two stellar sources, rather than multiplying or dividing them. Suppose there are two stars, A and B, with magnitudes m(A) and m(B), which appear so close together that their light blends into a single source. What is the magnitude of the resulting blend?
m(A + B) =? m(A) + m(B) NO!
The proper way to do this calculation is to convert the magnitudes back into intensities, add together the intensities, and then convert back into magnitudes. There's no way around it.
Q: My eyesight is so poor that I can't distinguish Alcor from
Mizar without my eyeglasses.
Given magnitudes of 4.00 for Alcor and 2.06 for Mizar,
what is the magnitude of the single blurry object I see?
Why do we continue to use this system? There are several reasons:
Astronomers who study objects outside the optical wavelengths -- in the radio, ultraviolet, or X-ray regimes -- do not have any historical measurements to incorporate into their work: these fields are all very recent, dating to the 1930s or later. In those regimes, measurements are almost always quoted in "more rational" systems: units which are linear with intensity (rather than logarithmic) and which become larger for brighter objects. In the radio, for example, sources are typically measured in janskys, where
1 Jansky = 10^(-26) watts / square meter / Hertz
A source of strength 5 Janskys is 5 times brighter than a source of 1 Jansky, just as one would expect.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.