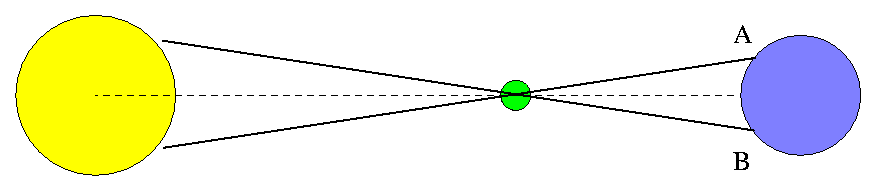
All information in this diagram has been ruthlessly altered for clarity.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
You can find more information on transits of Venus at
The simple example which follows is intended only to give you a flavor for the method; real astronomers in the eighteenth and nineteenth centuries included a host of complications and subtleties in their observations, measurements and analysis.
In the most basic terms, a transit of Venus permits scientists on Earth to draw a big triangle in the sky:

All information in this diagram has been ruthlessly
altered for clarity.
People at different locations on Earth will see Venus move across the Sun's disk on slightly different paths.
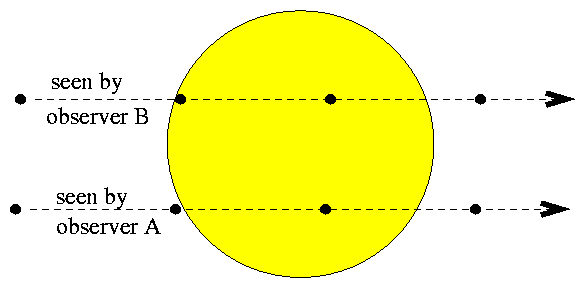
The difference in apparent paths is so-o-o-o exaggerated in
this diagram ....
So, in theory, finding the distance between the Earth and Sun -- the "solar parallax" -- is pretty simple:
Your job will be to observe the transit on a computer, using a planetarium program to simulate the view from two different locations on Earth. You should end up with two different pictures of Venus, taken simultaneously, which show a small displacement in its appearance relative to the Sun.
Once you've found the time of third contact, make an observation by printing a picture of the screen: go to the File -> Print menu.
Congratulations! You have succeeded in making one of the two crucial measurements.
The next step is to observe the same event from a different location on Earth. Let's pick Quito, Ecuador, which is very nearly due south of Harrisburg and Gettysburg.
Now you have two simultaneous measurements from two locations on Earth!
Just how large is the apparent shift in the position of Venus? This shift is called the "parallax angle", or "parallax" for short. Because Quito is nearly due south of Harrisburg, the shift in Venus' position should be nearly due north/south (which will simplify the analysis).
Your printouts may show many stars in addition to Venus and the Sun, but those didn't appear in real photographs, of course. To be fair to astronomers of yore, use the Sun as the only point of reference. On this date, it has a diameter of just over half a degree. To be precise, the diameter of the Sun during this transit is 1891 arcseconds. There are 60 arcseconds in one arcminute, and 60 arcminutes in one degree, which means 3600 arcseconds in one degree. Astronomers use arcseconds to measure small angles; it's more convenient to write "10 arcseconds" than "0.00277 degrees."

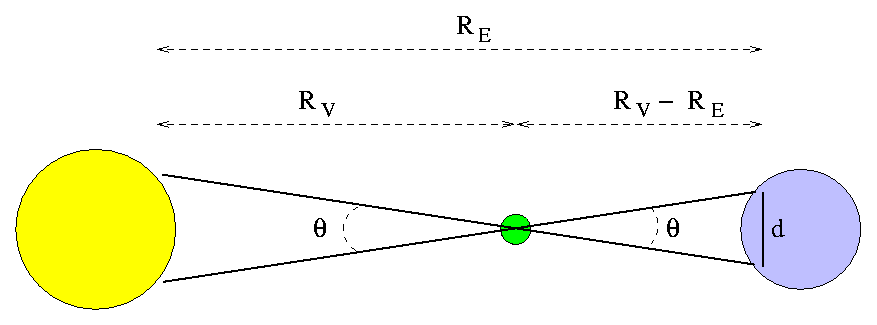
You have measured the parallax angle theta. If you can figure out the baseline distance d between the two locations on Earth, then you can use trigonometry to find the distance between Venus and Earth.
So, what is the distance d between Quito and Harrisburg?
Okay, so you have the distance d. How can that help you find the Earth-Venus distance? If the triangle defined by the parallax angle theta were a right triangle, it would be easy; but, alas, it's an isoceles triangle, not a right triangle. What can you do?
Great! Now use your trig skills. What is the distance between Earth and Venus?
At this point, you know the distance between Venus and Earth during the transit; but what we really want is the Astronomical Unit: the distance between the Earth and Sun. As you may recall, Kepler and other astronomers had figured out the relative sizes of the planetary orbits:
Planet Orbital period Orbital semi-major axis
(years) (AU)
----------------------------------------------------
Mercury 0.241 0.387
Venus 0.615 0.723
Earth 1.0 1.0
Mars 1.88 1.52
Jupiter 11.86 5.20
Saturn 29.46 9.55
----------------------------------------------------
Please don't forget that we've left out most of the nitty-gritty details in this very simple calculation. If you're within 10 percent of the real value, you've done a good job.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.