Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Let's go back and look again at our derivation of the dynamics of the universe in a previous lecture.
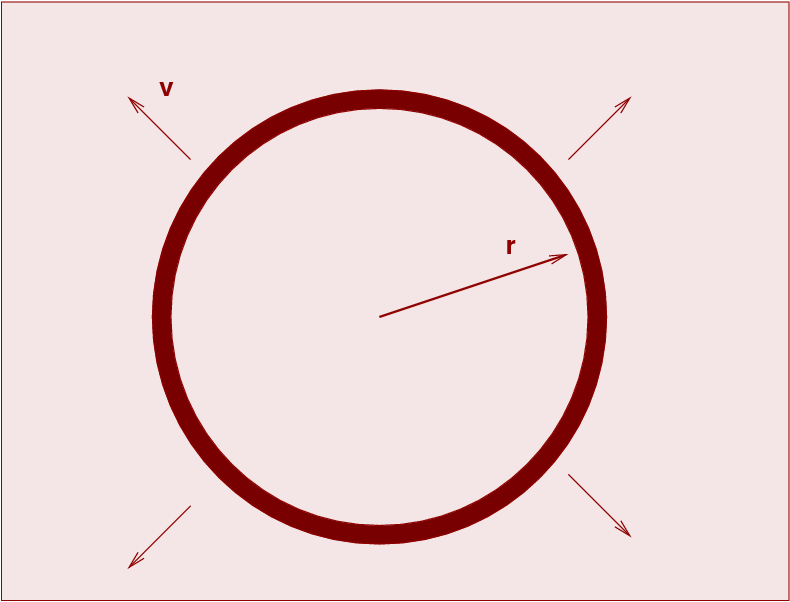
Imagine that the universe is homogeneous and uniform, filled with matter which has the same density everywhere. Let's write the density of material as ρ(t), so at the current time, it has value ρ(t0), Consider a spherical shell of material of radius r, which is currently expanding at velocity v.
What will happen to the shell as time progresses?
The answer isn't too hard to figure out. One can make a close analogy to the motion of a cannonball which is fired vertically upward from the Earth's surface. There are two possibilities from a practical standpoint, or three if one is a mathematician.
The same is true for this shell of material. Let us demonstrate.
Because the universe is uniform, the gravitational forces from all the material OUTSIDE the shell cancel each other. That means that the dynamics of the shell depend only on the total mass enclosed by it. We will assume that the peculiar motions of matter are so small, compared to the large-scale motion of the shell as a whole, that the interior mass doesn't change as the shell expands.
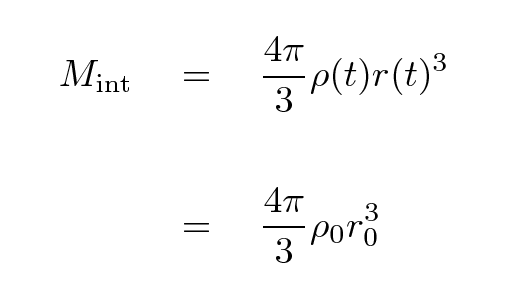
The shell itself has some mass m. We can write the total energy of the shell as a sum of its kinetic and gravitational potential energies. For reasons which will become clear later, I'll write that total energy in one particular manner.
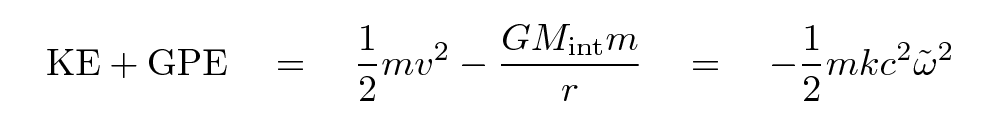
Q: Derive the force associated with the gravitational
potential energy term in the equation above.
How does this force affect the motion of an object?
Okay, this is where things will get a little different.
Now, back in the day (1917), when Einstein was going through a relativistic version of this analysis, he realized that the version you see above would yield non-stationary solutions. That is, he realized that a universe governed by these physical laws would NOT be static. It could expand, or contract, but it couldn't remain fixed in size.
Unfortunately, this date -- 1917 -- was still a decade before Hubble and Humason and other observers began to see the evidence for expansion. As far as Einstein knew,
So, in order to cause the theory to agree with the observations (of that day), Einstein modified the equation by adding one term.
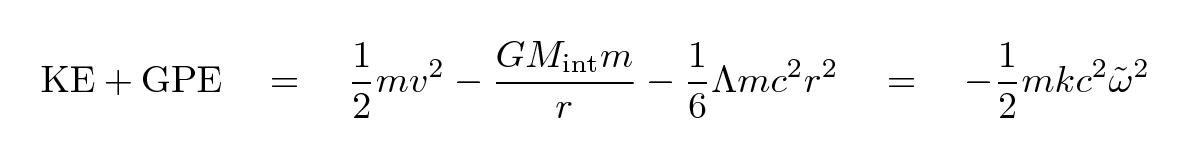
Q: What are the units of Λ?
This new term acts like a potential energy. It must therefore have an associated force.
Q: Derive the force associated with this potential
energy.
How does this force affect the motion of an object?
Right. The cosmological constant terms adds a force which pushes radially outward. That's exactly what Einstein needed in order to counteract the force of gravity.
If one works through the equations of motion with this new term, one will find that the deceleration parameter q is no longer a simple function of the matter density alone, but depends on both the matter density and on Λ.
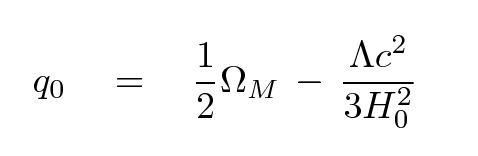
Q: The value of q0 is uncertain,
but current estimates lie not too far from 0.
What is the value of Λ?
On what size scales might we expect to see evidence
for Λ?
Just as we speak about the density of matter in two different ways,
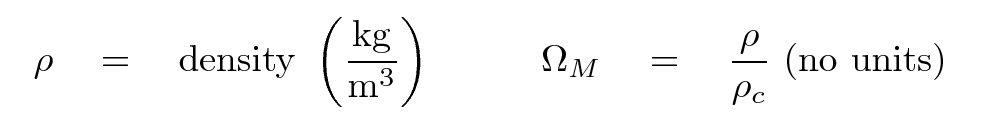
we can also discuss the cosmological constant in two ways, the second of which is both normalized to the "critical" value and unitless.
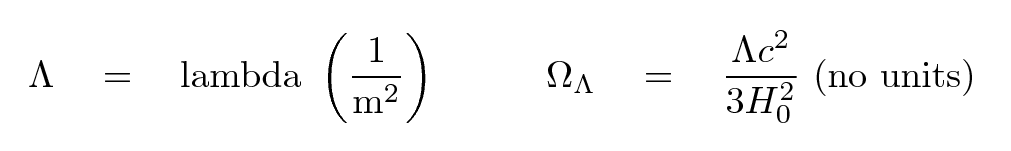
Okay, so we've added a new parameter to the list of cosmological quantities. What effect does it have on the evolution of the universe?
The simple answer is "it fights against the pull of gravity". If the density of matter in the universe is just a bit larger than the critical value, we would expect the universe to cease expanding and collapse on itself; but if Λ is larger than zero, it can cause the universe to keep expanding.
Let's play around a little.
Thanks to
The Smithsonian
What else can we say about Λ in a qualitative way?
The large-scale geometry of the universe, its curvature, if you prefer to think of it that way, depends on both the amount of matter and on Λ. In fact, the curvature of the universe depends on the sum of
If there is a non-zero cosmological constant, then computing the distance to some object becomes a complex operation. A good source for information on this topic is Carroll, Press and Turner, ARA&A 30, 499 (1992).
Following those authors, we can compute the distances to an object at a redshift z1 in the following manner.
First, we calculate another version of omega,
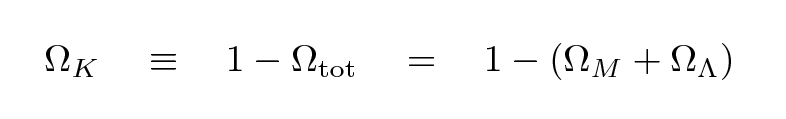
Next, we use it to help us compute the following integral
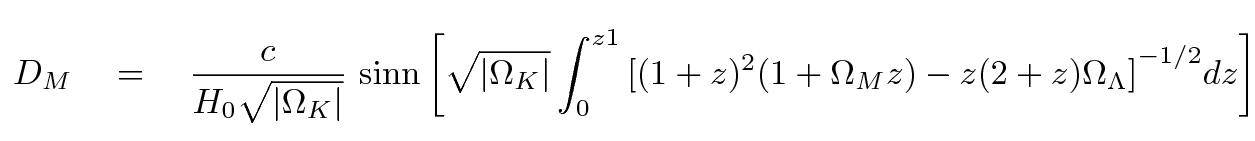
Here, the function labelled "sinn" stands for three different functions, depending on the value of Ωtot.
Phew. That was the hard part. This quantity DM is sometimes called the "proper motion distance." It is related to the other distances we have used in the following way:
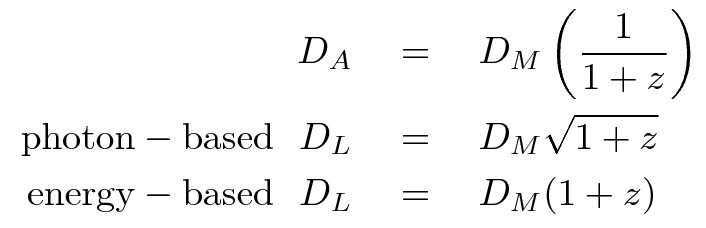
You can see that calculating distances in a universe which has a non-zero cosmological constant is a pain in the neck....
Alas, it's not a simple matter to disentangle the values of the matter density and the cosmological constant using the classic distance-magnitude relationship. For example, look at this very nice dataset:
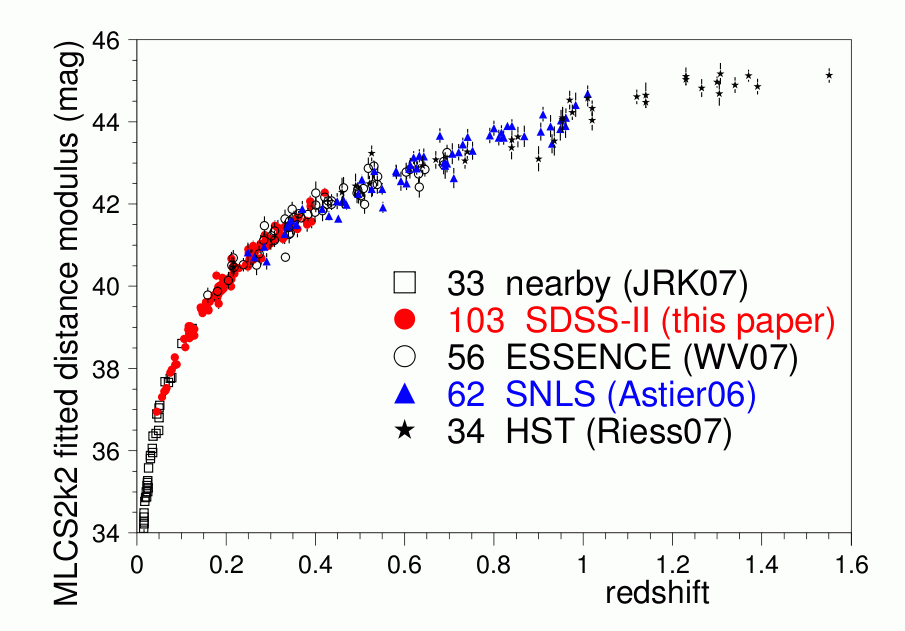
Figure taken from
Kessler et al., ApJS 185, 32 (2009)
These measurements of supernova distances reach from redshift zero to redshift 1.6, but they still aren't really enough. The problem is that a slightly larger value of ΩΛ has sort of the same effect as a slightly larger value of ΩM.
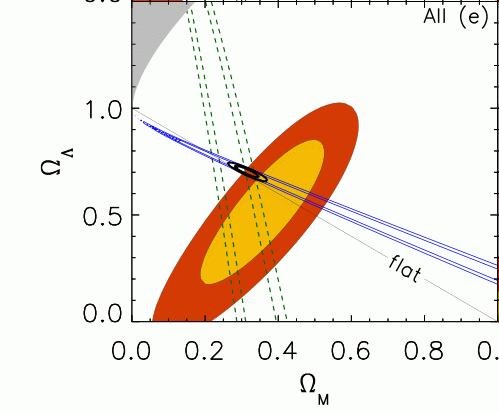
Figure taken from
Kessler et al., ApJS 185, 32 (2009)
Fortunately, there are very different types of tests we can make, using observations of the CMB or the clustering of galaxies, which provides information on the cosmological parameters in a different manner. In the figure above, the blue lines labelled "flat" denote the region of parameter space which is consistent with measurements of the CMB. The intersection of the blue region with the red-and-gold region -- the portion of parameter space which is consistent with both
ends up being pretty darn small. At the time of writing, the astronomical community has settled on a "standard model" which has value of roughly
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.