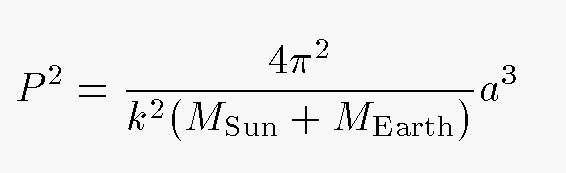
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
A decade after announcing his First and Second Laws of Planetary Motion in Astronomica Nova, Kepler published Harmonia Mundi ("The Harmony of the World"), in which he put forth his final and favorite rule:
Kepler's Third Law: The square of the period of a planet's orbit is proportional to the cube of its semimajor axis.
It turns out that this relationship will serve as the basis for our attempts to derive stellar masses from observations of binary stars ... but notice how the Third Law itself never mentions mass!
Let's check to see just how well Kepler's Third Law works. I'll do the first example:
Earth: period P = 1 year
semimajor axis a = 1 AU
2 3
P = (const) a
---> const = 1 for this choice of units
Now, you verify that if you continue to use the same units -- period in years, semimajor axis in AU -- these other orbits also satisfy the same equation:
2 3
P = 1 * a
Hmmmm.... this Third Law doesn't seem to work all the time, does it? Or is there something we're missing?
It turns out that the constant in Kepler's Third Law depends on the total mass of the two bodies involved. Kepler himself, studying the motion of the planets around the Sun, always dealt with the 2-body system of Sun-plus-planet. The Sun is so much more massive than any of the planets in the Solar System that the mass of Sun-plus-planet is almost the same as the mass of the Sun by itself. Thus, the constant in Kepler's application of his Third Law was, for practical purposes, always the same.
But in the case of the Moon's orbit around the Earth, the total mass of the two bodies is much, much smaller than the mass of Sun-plus-planet; that means that the value of the constant of proportionality in Kepler's Third Law will also be different. On the other hand, if we compared the period and semimajor axis of the orbit of the Moon around the Earth to the orbit of a communications satellite around the Earth, we would once again have (almost) the same total mass in each case; and thus we would end up with the same relationship between period-squared and semimajor-axis-cubed.
To make a long story short -- we'll tell the whole story later, including a derivation of the formula below from Newton's Law of Gravitation -- one can write Kepler's Third Law in the following way:
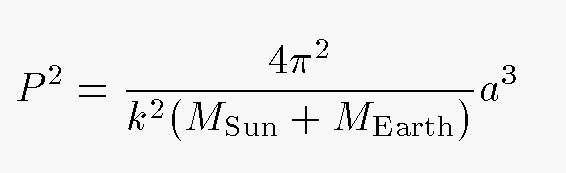
or
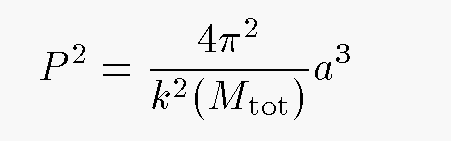
The constant k in the equations above is known as the Gaussian gravitational constant. If we set up a system of units with
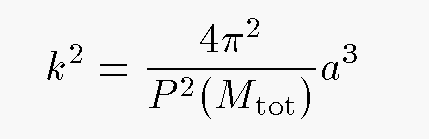
Exercise: What is the value of the Gaussian gravitational constant k?
The key point here is that the only measured quantity we need to find k is time: the period of the Earth's orbit around the Sun. Now, it's not quite so easy as it sounds, but it can be done without too much trouble. Moreover, because we can average over many, many, many years, we can determine the length of the year very accurately -- to many significant figures. Therefore, we can also determine the value of k to many significant figures. If all we want to do is calculate the orbits of objects around the Sun, then k is all we need; and with a very accurate value of k, we can calculate very accurate planetary orbits.
For example, it was this constant k that Adams and Leverrier used in their computations of the as-yet-unknown planet VIII, aka Neptune.
At this point, you may be thinking, "Hey, wait a minute -- isn't that constant k just another way of writing the Newtonian Constant of Universal Gravitation, G?" Well, the answer is yes, and no:
The Gaussian constant, k, is defined in terms of the Earth's orbit around the Sun. The Newtonian constant, G, is defined in terms of the force between two two masses separated by some fixed distance. In order to measure k, all you need to do is count days; in order to measure G, you need to know very precisely the masses, separation, and forces between test objects in a laboratory. The Gaussian constant is obviously much easier to determine. Look at a sample pair of values from recent compilations:
k = 0.01720209895 (10 significant digits)
-11
G = 6.6742 x 10 (5 significant digits)
Physicists are still arguing over the fifth digit of G!
If the laws of physics are the same everywhere in the universe, as we think they are, then we can use Kepler's Third Law to measure the mass of a distant star around which a distant planet orbits. All we need to do is measure
But how sensitive will our result be to small errors of measurement? Suppose we measure the following quantities for a planet orbiting some star:
What is the mass of the star in this system? What is the uncertainty in the mass? Express your result in absolute terms (solar masses), and in percentage terms.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.