Examples of Numerical Attacks on Hard Problems

For thousands of years, humans recognized a small number of objects in the night sky which moved against the backdrop of the fixed stars. We call them "planets." In addition to the Sun and Moon, five were known to the ancient world: Mercury, Venus, Mars, Jupiter and Saturn. In 1781, a professional musician (and amateur astronomer) named William Herschel discovered a new planet during his systematic sweeps of the heavens. We now call it "Uranus".

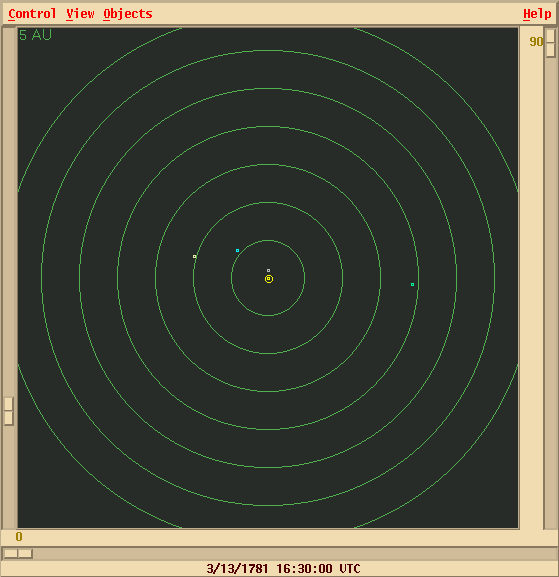
A bird's-eye view of the solar system from far above the plane of the ecliptic shows the location of Uranus at the time of its discovery (Uranus is the green dot near 3 o'clock, the Earth the white dot just above the Sun at center; Jupiter and Saturn are also shown).

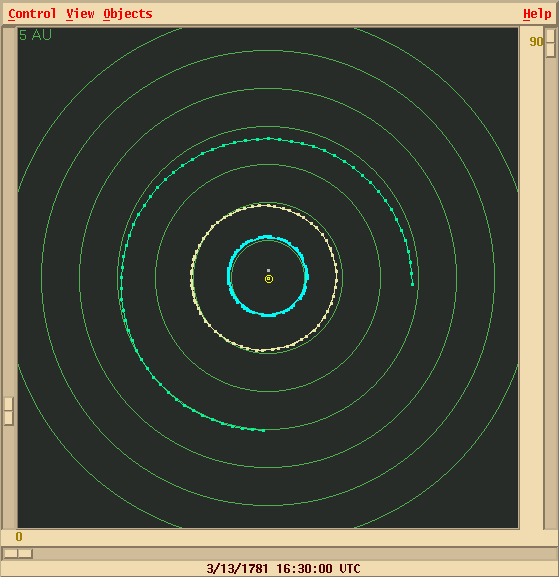
Astronomers followed the motions of Uranus and the other planets over the succeeding decades. By 1845, Uranus had moved about three-quarters of the way around the Sun in its orbit:

Thanks to Newton's Law of Gravitation, scientists could calculate exactly how the planets ought to move in their orbits. One can form an EXACT solution when there are just two bodies orbiting around each other: each moves in an elliptical path. The Sun is so much more massive than all the other bodies in the solar system that its influence dominates all motions. One can very quickly determine how a planet ought to move due to the Sun's attraction alone. Astronomers quickly discovered that their measurements were precise enough to show the very small perturbations to these ellipses. With a great deal of effort, it was possible to calculate the forces on each planet due to the Sun AND the other planets. Remember, this was way back in the days before computers, or calculators; the work took pencil and paper and days of drudgery.

During the 1820s and 1830s, a few astronomers noticed that Uranus wasn't quite following the expected orbit. Even after accounting for the influences of all the other planets, they could not predict its position precisely. The measured positions of Uranus were slightly ahead of the predicted ones for the first forty or so years after its discovery, and slightly behind the predicted ones for the next few decades.

What was going on?

Two young scientists, John Couch Adams in England, and Urbain Jean Joseph Leverrier in France, independently -- and unknown to each other -- considered the possibility that there was another planet, farther from the Sun than Neptune, which might cause the observed perturbations. If the planet started in just the right position, ahead of Uranus in their orbits, it would pull Uranus forward at first (from 1781 to 1802):

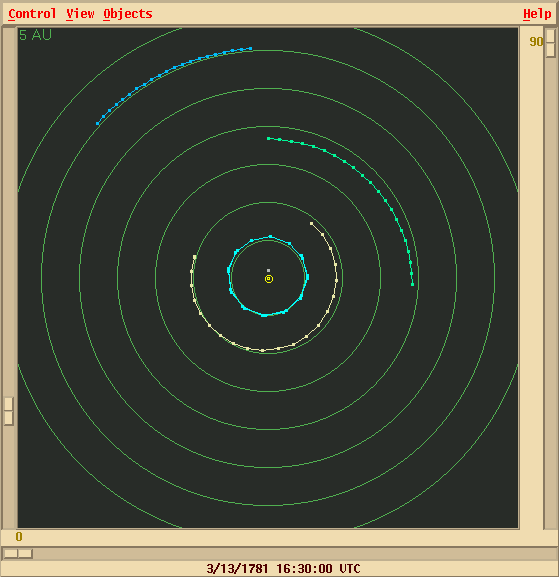
Then have little effect while Uranus passed it (from 1802 to 1823):

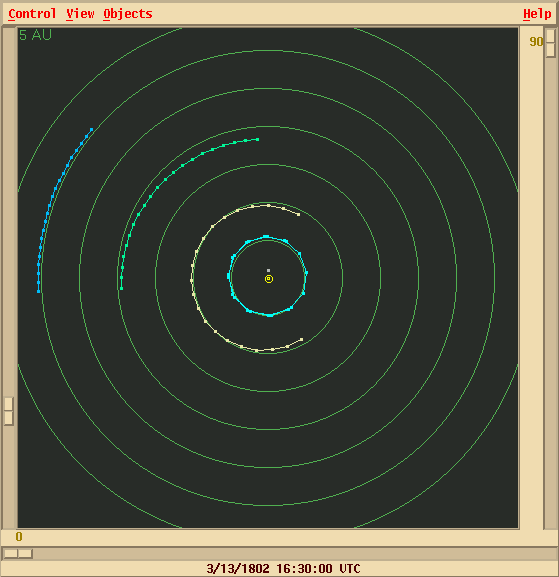
And later still (1823 to 1844), after Uranus had passed it, it would slow Uranus down:

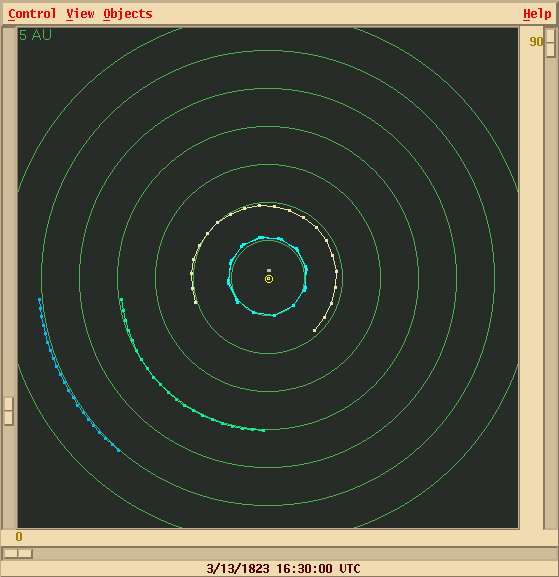
During the 1840s, Adams worked out where the new planet might be. In September, 1845, he wrote to Sir George Biddell Airy, the Astronomer Royal of England, asking for his help in searching for an object near his predicted position. Airy -- to be brief -- did nothing about it.

Leverrier, on the other hand, who started a few years after Adams, soon had a prediction of his own. In June, 1846, Leverrier published a paper in which he provided details of his work and a predicted position. His position was just two degrees away from that of Adams -- but he still didn't know of Adams' work. When Airy learned of Leverrier's paper, he asked a colleague to start looking for the new planet, but nothing happened for three weeks. In late July, 1846, one English astronomer (John Challis) started searching near the predicted position -- though without much enthusiasm.

On August 31, 1846, Leverrier (still ignorant of Adams' work) published another paper with an improved position.

On September 2, 1846, Adams sent an improved position of his own to Airy.

On September 18, 1846, Leverrier wrote a letter to a friend of his at the Prussian Observatory in Berlin, asking him to use the telescope there to search for the new planet at his calculated position. His friend, Johann Gottfried Galle, received the letter on September 23. Galle and his assistant, Heinrich d'Arrest, started work that evening. Galle looked through the telescope and called out the positions of stars, while d'Arrest checked them off against a chart.

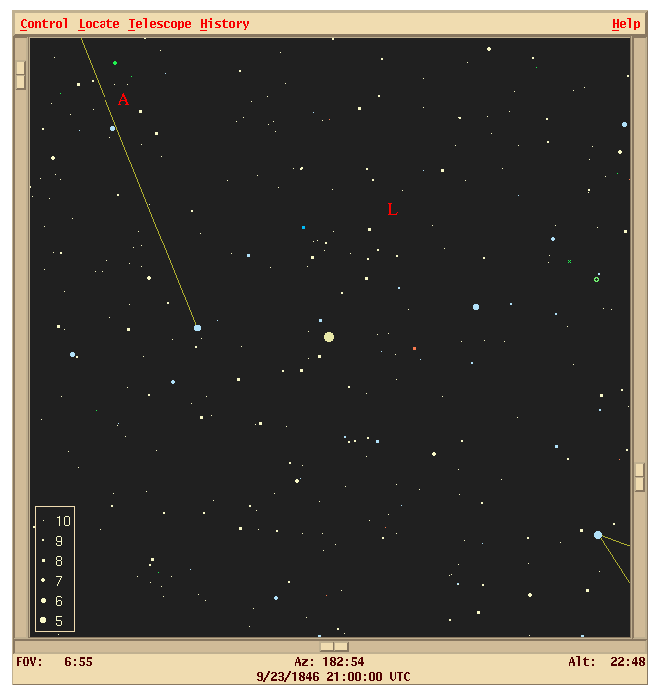
Below is shown an area of the sky about seven degrees across, as it appeared on September 23, 1846. The view is similar to what one would see looking through a pair of ordinary binoculars. The bright object at the center of the field is Saturn. Adam's predicted position is marked with an "A", and Leverrier's position with an "L".

Less than an hour after they started, they found it: a star which was not on the charts:

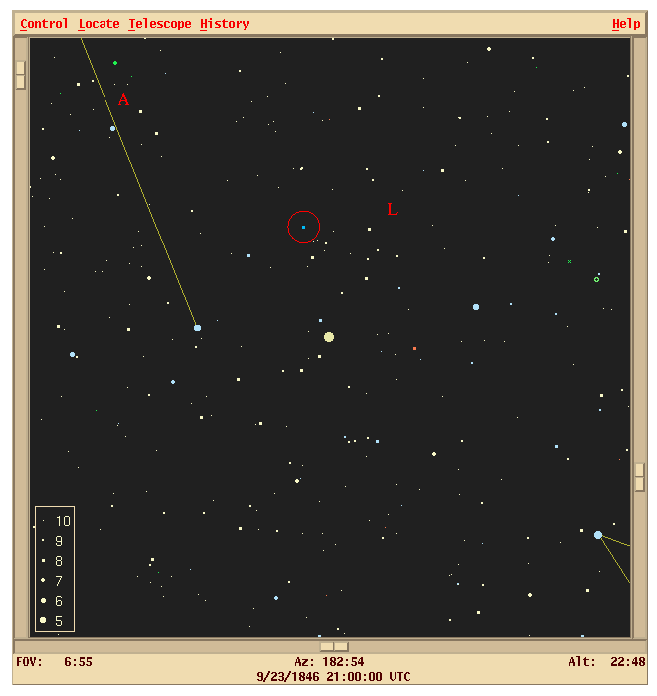
Leverrier was hailed as a hero, the discoverer of a new world, eventually called "Neptune." Eventually, Adams' work was also recognized, and today we consider both Adams and Leverrier to be the co-predictors of the eighth planet.

For further reading about the prediction and discovery of Neptune, visit Mathematical discovery of planets.

Later in this course, you will have your own chance to use Newton's Law of Gravity to calculate the position of a planet as it moves around the Sun. Your job is much easier than Leverrier's or Adams': you will be able to give all the mind-numbing calculations to a computer, you may restrict the motions to two dimensions, and you need only consider two bodies, not eight or nine. Still, you may find it a challenging task...

The Hundred Dollar Challenge

Mathematics has a long series of famous puzzles posed by famous mathematicians; some have been solved, some have not. In 1696, for example, Johann Bernoulli published a paper which started as follows:

I, Johann Bernoulli, address the most brilliant mathematicians in the world. Nothing is more attractive to intelligent people than an honest, challenging problem, whose possible solution will bestow fame and remain as a lasting monument. Following the example set by Pascal, Fermat, etc., I hope to gain the gratitude of the whole scientific community by placing before the finest mathematicians of our time a problem which will test their methods and the strength of their intellect. If someone communicates to me the solution of the proposed problem, I shall publicly declare him worthy of praise.
...
Given two points A and B in a vertical plane, what is the curve traced out by a point acted on only by gravity, which starts at A and reaches B in the shortest time.

This problem became known as the brachistochrone, meaning "fastest falling." Among those to tackle the puzzle was Isaac Newton, who managed to solve it in under twelve hours! Newton's solution was published anonymously, but Bernoulli wrote that its author was obviously Newton: ex ungue leonem, "from its claw (one recognizes) the lion."

You can read more about the history of (and solution to) the brachistochrone problem. It turns out that this problem can be solved analytically, in several ways.

A modern example of the "puzzle challenge," directed specifically at numerical techniques, was announced in Volume 35, Number 1, of ``SIAM News'':

www.siam.org/siamnews/01-02/challenge.pdf
or try a local copy

Nick Trefethen of Oxford University offers, not fame and praise, but cold, hard cash.

Each October, a few new graduate students arrive in Oxford to begin research for a doctorate in numerical analysis. In their first term, working in pairs, they take an informal course called the "Problem Solving Squad." Each week for six weeks, I give them a problem, stated in a sentence or two, whose answer is a single real number. Their mission is to compute that number to as many digits of precision as they can.
Ten of these problems appear below. I would like to offer them as a challenge to the SIAM community. Can you solve them?
I will give $100 to the individual or team that delivers to me the most accurate set of numerical answers to these problems before May 20, 2002. With your solutions, send in a few sentences or programs or plots so I can tell how you got them. Scoring will be simple: You get a point for each correct digit, up to ten for each problem, so the maximum score is 100 points.
Fine print? You are free to get ideas and advice from friends and literature far and wide, but any team that enters the contest should have no more than half a dozen core members. Contestants must assure me that they have received no help from students at Oxford or anyone else who has already seen these problems.
Hint: They're hard! If anyone gets 50 digits in total, I will be impressed. The ten magic numbers will be published in the July/ August issue of SIAM News, together with the names of winners and strong runners-up.

Several of the problems are simple enough for you to attack with the knowledge you'll learn in this course. For your final project, you must choose a problem to work on in small groups. Any of the Hundred Dollar problems would qualify, or you may devise your own problem.

Last modified Mar 11, 2002 by MWR.