
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
We need to find new methods to reach out father into space, well beyond the Milky Way Galaxy and outside the Local Group. If we wish to measure the distance to a galaxy in the Virgo Cluster, for example, we have to leave fundamental methods behind and start to adopt more indirect techniques.
As you will see, some of the methods described here are called secondary distance indicators because we
These methods are not as secure as the direct ones --- they make our ladder begin to tilt and sway. But sometimes, these secondary methods are the best we can do.
Let's look at the HR diagram of a group of stars, all born at the same time, with identical chemical compositions. I'll choose a metal-poor population, with
This should be relatively typical of an old stellar population, like that in the halo of our Milky Way, or the halo of other galaxies.
To make models of stars as they evolve, I'll use the
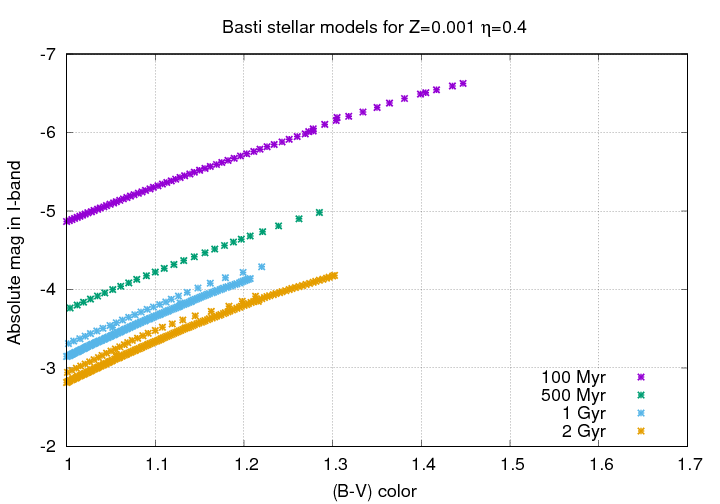
The site provides a set of stars with masses varying from 0.5 to 8.4 solar, and follows them as they evolve into the red giant branch.Let's begin with very young stellar populations. The figure below shows the HR diagrams for clusters of stars with ages of 100 and 500 Myr.

Q: What changes do you see between 100 and 500 Myr?
Q: What happens to the magnitude of the most
luminous red giants as the cluster ages?
Now, as time passes, the stars continue to evolve ... but the rate of change decreases. This is simply a result of the longer lifetimes and slower evolution of the lower-mass stars which remain.

But not only does the pace of change slow down -- something rather peculiar, but very, very useful for astronomers, is happening at the tip of the red giant branch.
Q: What happens to the tip of the red giant branch
between 1 Gyr and 2 Gyr?
Let's zoom in on this region. One thing you'll notice is a set of parallel tracks for the stars of each age. In those cases, the lower, more solid track shows stars of slightly lower mass, which are just ascending the red giant branch (RGB) for the first time, and then starting to descend it; the upper, more sparse track shows stars of slightly higher mass, which are making a second journey up the red giant branch before they leave for good (probably turning into planetary nebulae). The track of those making their second trip is sometimes called the Asymptotic Giant Branch (AGB).
If we look at even older groups of stars, we will see that this tip of the RGB becomes redder .... but remains roughly the same luminosity.
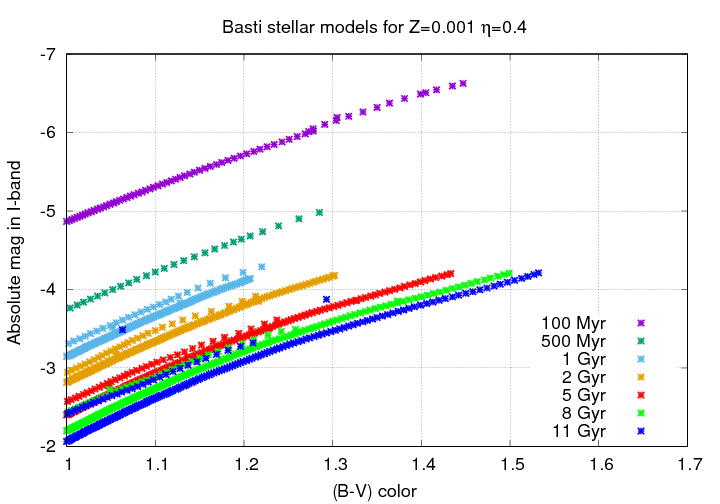
The absolute magnitude of this Tip of the Red Giant Branch is nearly constant from 5, to 8, to 11 Gyr.

Now, I've cheated just a little bit. If you look closely, you'll see that on the y-axis of these graphs, I've put the "absolute magnitude in I-band," rather than the more common "absolute magnitude in V-band." It turns out that in the V-band, the absolute magnitude of this tip does change a bit more strongly, growing fainter as time passes:

Astronomers have examined the possibilities, and it seems that the I-band is just the wavelength at which these red giants of different ages appear to have about the same luminosity. I don't know exactly why that is, but it's certainly convenient for us ground-based observers!
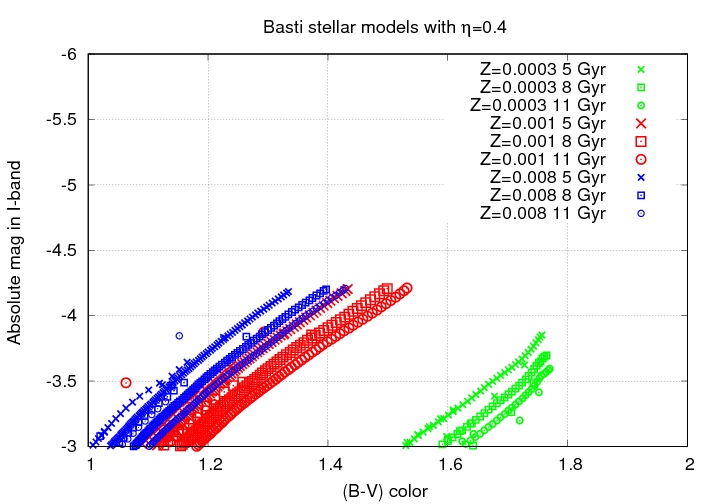
Of course, it's not perfect. If we look at models with different metallicities, we see that there IS some variation in the level of the TRGB, but only for very metal-poor populations.
This method was first described back in 1993
which I'll use as a source for the following material.
The method has been refined and extended over the past two decades. A few good recent articles are
The basic idea is pretty simple:
Here's an example. The galaxy NGC 1365 is relatively nearby, so we can resolve individual stars with HST. The purple squares mark the location of some images taken by HST in 2013.

Here's a copy of one of those HST images, which you can grab for yourself from the Hubble Legacy Archive.
Let's zoom in one small region, away from the spiral arms:

If we set the image contrast so that it shows only the very brightest objects ... we don't see very many.

But if we lower the threshold, a few more stars appear.

Lowering the threshold further makes a few more stars appear ...

... but when we reach a certain point, suddenly a WHOLE BUNCH of stars appear, all at once. We have finally reached the level of the TRGB. (Click the image below to animate the sequence)
Now, let's look at how Jang et al., arXiv:1703.10616 put this into a quantitative form. They begin by making a color-magnitude diagram of stars in the images:
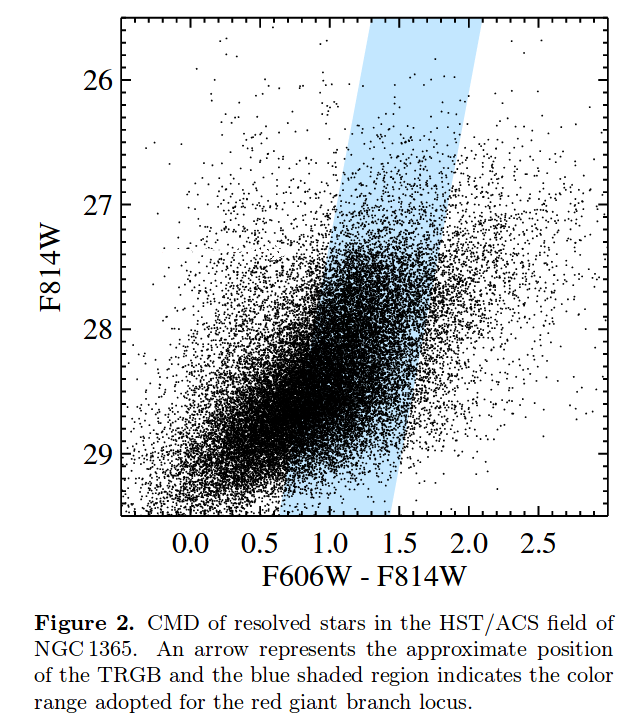
Figure 2 taken from
Jang et al., arXiv:1703.10616
and slightly modified.
Q: Based on this CMD, what is the apparent magnitude
of the TRGB?
Q: Using that apparent magnitude, and absolute magnitude
MI = -3.95 for the TRGB,
what is the distance to NGC 1365?
The authors make a histogram of number of stars as a function of magnitude, smooth that histogram, and finally apply a matched filter to find the precise value at which stars suddenly increase in number.
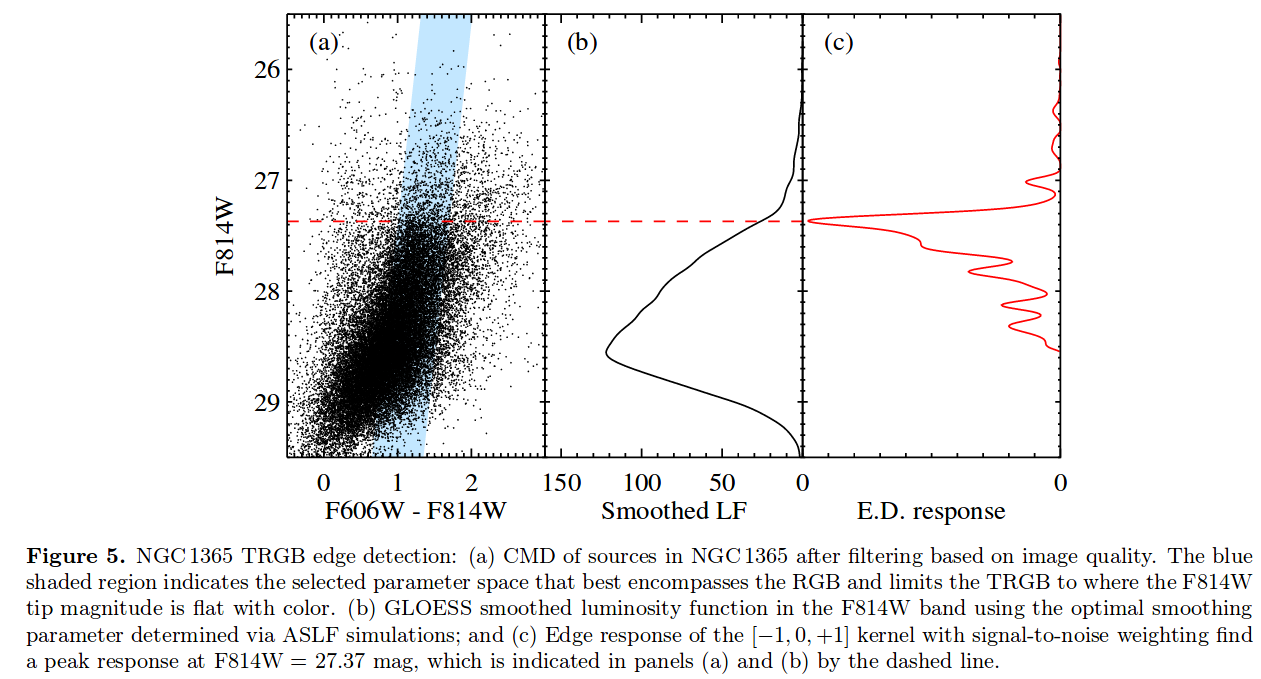
Figure 5 taken from
Jang et al., arXiv:1703.10616
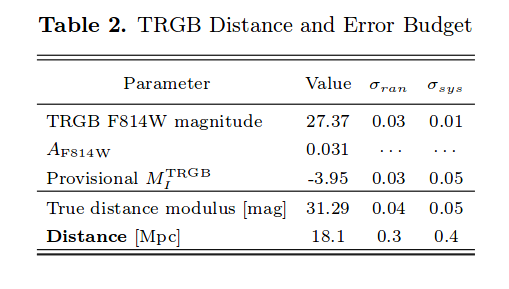
Table 2 taken from
Jang et al., arXiv:1703.10616
Another recent paper by this same group
uses TRGB to measure the distance to M60, a giant elliptical galaxy in the Virgo Cluster. In that case, the color-corrected F814W apparent magnitude of the TRGB is found to be m814W = 27.04, leading to a distance modulus of (m - M) = 31.05, or a distance of 16.2 Mpc.
Thus, in the past few years, we have managed to just barely reach two of the nearest cluster of galaxies, Virgo and Fornax, with TRGB. We can use TRGB to check the distances based on other methods, since it is independent of (for example) the physics of pulsing stellar atmospheres.
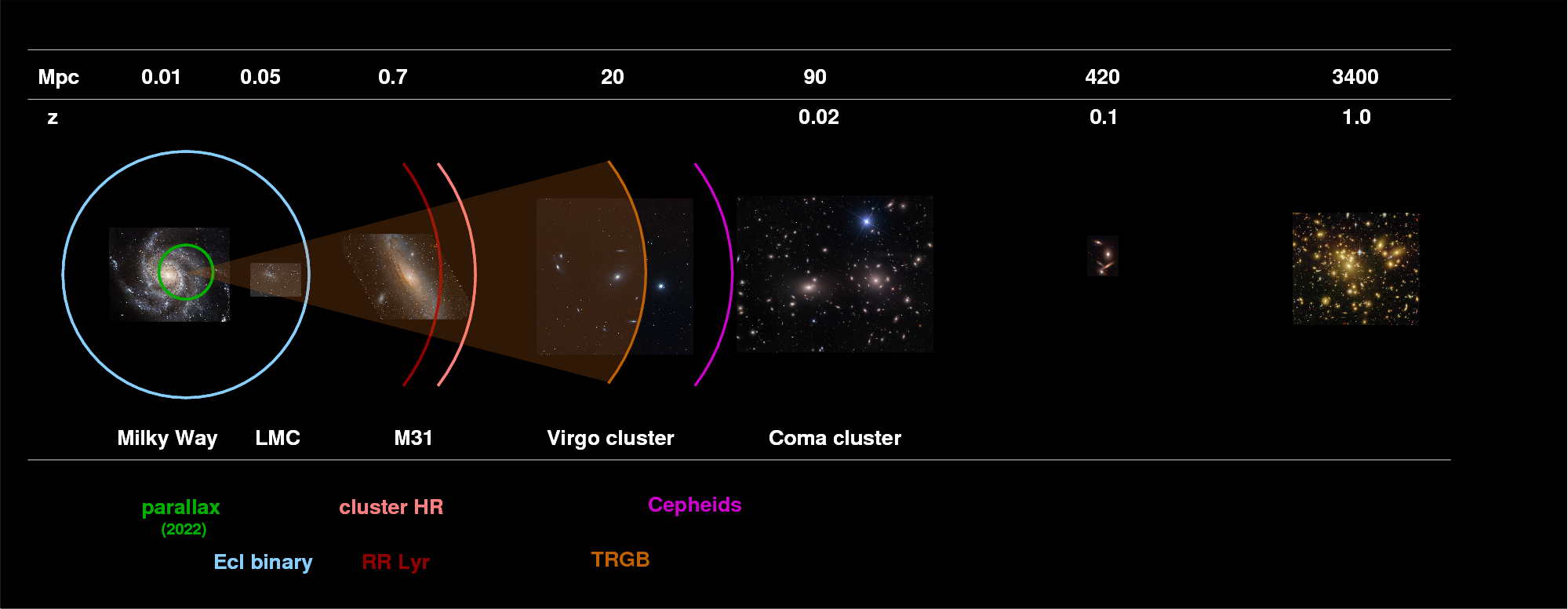
As the diagram above shows, the Coma Cluster of galaxies lies farther away than Virgo and Fornax. Because Coma is a much more rich and massive collection of galaxies, it could serve as a good "nearby" example of the many rich clusters we see at moderate and high redshits. In addition, there are some secondary distance indicators which we can measure (or have measured) in Coma -- so it would be very nice if we could measure the distance to this cluster in order to calibrate them accurately.
So, could we detect TRGB stars in Coma?
Well, the problem is that, at the distance of Coma, the TRGB feature might be difficult, or impossible, to detect. Several different pieces of evidence suggest that the distance modulus of Coma is probably about 3.8 magnitudes larger than that of Virgo or Fornax. Consider again this color-magnitude diagram of stars in a member of the Fornax Cluster.

Figure 2 taken from
Jang et al., arXiv:1703.10616
and slightly modified.
Q: At what magnitude would the TRGB appear in a galaxy in
the Coma Cluster?
That's really, really, REALLY faint.
One way to quantify the difficulty of detecting stars this faint is to focus on the "signal-to-noise" ratio of our measurements of stellar brightness. The measurements of Jang et al., arXiv:1703.10616 were made with the Hubble Space Telescope; let's pretend that the exposure time of all the images used to build that color-magnitude diagram was 10 hours. Now, one way to detect fainter objects would simply be to increase the exposure time ... but the competition for time on space telescopes is always fierce. Let's accept that we must settle for new measurements which require exactly the same amount of exposure time.
Q: Aside from increasing the exposure time, is there any other
way to detect fainter stars in this galaxy?
Of course there is: build a bigger telescope! And -- hey, presto! There's a new, bigger space telescope in orbit right now! The James Webb Space Telescope has a mirror of diameter 6.5 meters, considerably larger than the 2.4-meter mirror of HST. Is JWST large enough that it can detect the TRGB in the Coma Cluster in a 10-hour exposure?
We can apply some math and statistics to address this question. The issues of signal and noise involved in stellar photometry can be rather involved; if you want lots of details, you can read other material
For our discussion here, we can simplify things to the following quantities.

The signal-to-noise ratio is, in this simplified case, approximately

Now, in the case of HST and Fornax, the measurements are good enough that we can detect and measure the location of the TRGB pretty well. Let's demand that our measurements of stars in the Coma Cluster have exactly the same signal-to-noise ratio -- that ought to allow us to determine the magnitude of the TRGB just as accurately.
The stars in Coma are fainter, by about Δm = 3.8 mag, so they will produce fewer photons by a factor
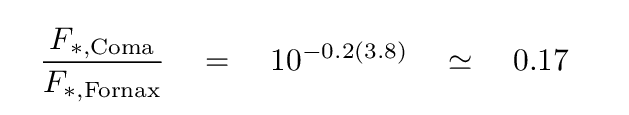
But, unfortunately, the background of images taken in Coma will NOT be much fainter; in fact, it will be roughly the same as that for images in Fornax.
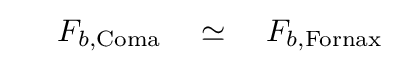
If we assume identical exposure times, then in order for the signal-to-noise ratios to be the same, we would need to use a telescope of radius R such that
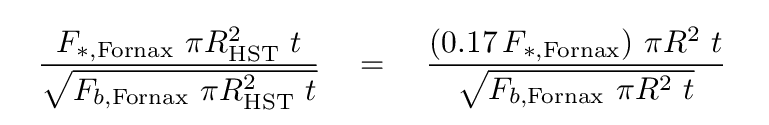
In other words, we would need to use a telescope with radius R given by
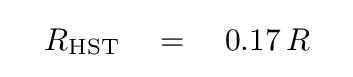
Q: The diameter of HST is about 2.4 meters. How large would a new
space telescope need to be in order to detect
the TRGB in Coma with an identical exposure time?
Q: The diameter of JWST is about 6.5 meters. Is JWST large enough
to do the job?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.