Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Many stars in the sky are part of multiple-star systems, in which two or three or four stars orbit around each other, on timescales of hours to centuries. In a few, very special cases, detailed observations of binary stars which eclipse each other can be used -- together with a bit of theory -- to measure the distance to the system.
In today's lecture, we'll discuss in some detail how binary stars with JUST the right properties, and with a LOT of observations, both photometric (easy) and spectroscopic (hard), can yield very secure distances.
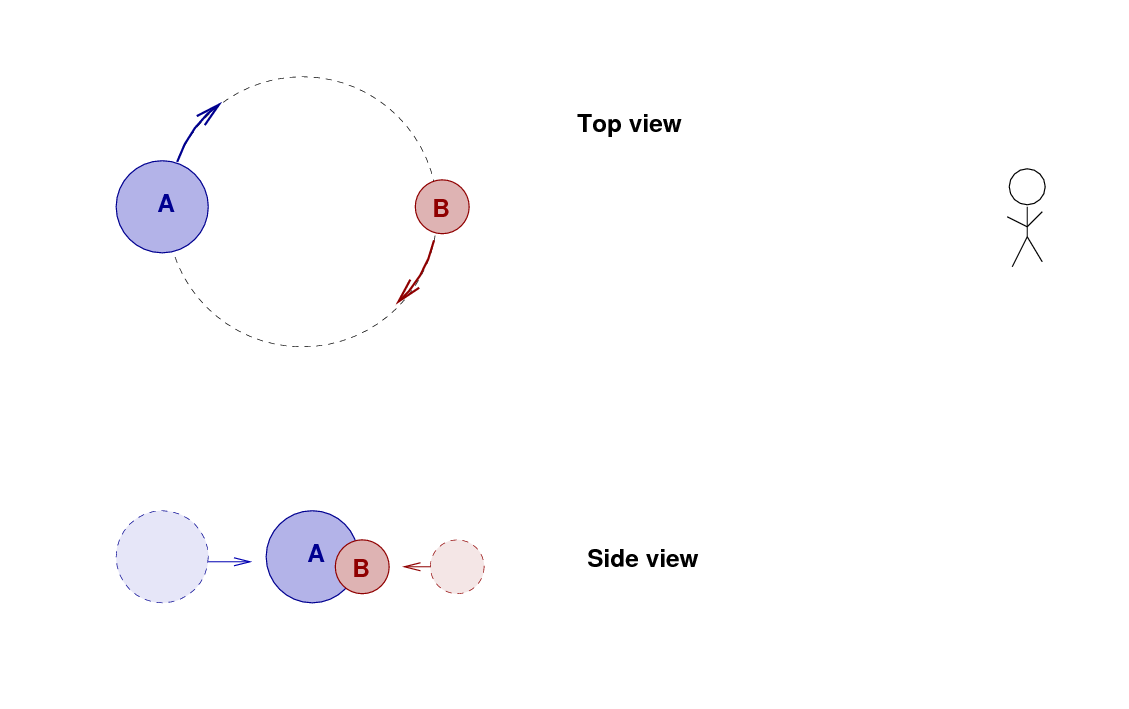
Consider a pair of stars in a binary system, orbiting around their center of mass. If we are very lucky, and the following conditions are ALL met,
then we can use geometry and one solid bit of physics -- the spectrum of radiation emitted by a hot gas -- to determine the distance to the binary system. Here's how we do it.
Suppose that two stars orbit each other in such a way that we see them pass in front of each other.
If we measure the light from the system over one full orbital period, then we'll see one dip in the brightness as star B passes in front of A, and then a second dip when A passes in front of B.
How can we use these binary stars to measure distances? We need to determine a number of parameters; we can divide the work into several steps.
Step II
Step III
The first step is pretty simple, and it doesn't involve a great deal of expertise. The second step is NOT simple, since stars do NOT emit like blackbodies at the level of accuracy which we need for this calculation. The third step is again pretty simple, though there can be complications due to extinction and reddening.
To see just how this theory plays out in practice, let's give it a try outselves. We'll use data from the paper
If we follow all the steps, we ought to be able to determine the distance to one of our Milky Way's nearest neighbors: the Large Magellanic Cloud.
Image of Magellanic Clouds and the Paranal Observatory
courtesy of
Y. Beletsky/ LCO/ESO.
Let's go through the first step: finding the size of each star. Examine the figure below, which shows the radial velocity of each star in the system as a function of time.
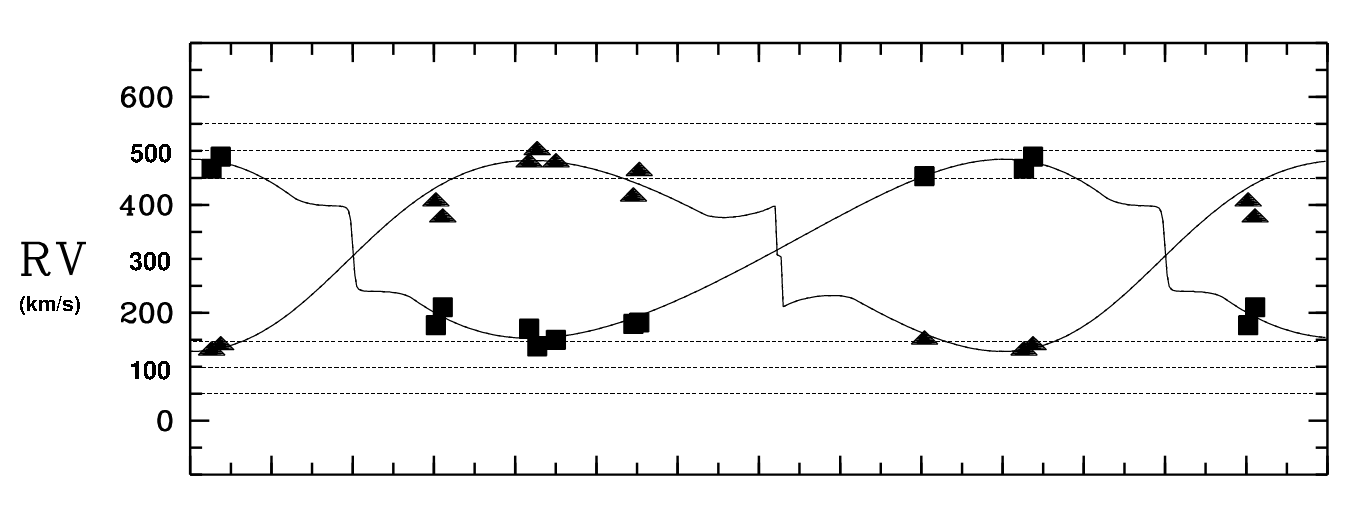
Figure 1 taken (and slightly modified) from
Guinan et al., ApJ 509, 21 (1998)
Q: What is the orbital speed of each star
around the center of mass?
You may pretend that the orbits are circular
and equal in amplitude for this exercise.
Our next step is to measure the duration of the eclipse. Examine the figure below, which shows the light curve of the binary. The period of the system is P = 5.73 days.
Figure 1 taken (and slightly modified) from
Guinan et al., ApJ 509, 21 (1998)
Q: How long does the secondary eclipse at
orbital phase 0.5 last? Call this duration Δt,
and express your answer in seconds.
Recall that the period is P = 5.73 days.
Right. We're almost ready to compute the size of each star. Look closely at the motion of the two stars as the eclipse happens. Since the two stars are moving in opposite directions as they pass each other, their RELATIVE speed is simply (vA + vB). Let's fix the star B in place, and watch as the star A moves across it from right to left at this combined speed. During the time period from first to fourth contact, the star A must move a distance of RB + RA + RA + RB.
Now, in this particular case, both stars turn out to be roughly the same size, so let's approximate RA = RB. In addition, the velocities of the two stars around the center of mass are also roughly equal in this system, so we can also write vA = vB.
With our approximations -- which, of course, the authors of this study do NOT make -- we end up with a simple means to determine the radius of each star:
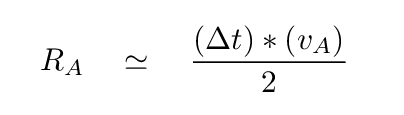
Q: What is the size of each star? You may
pretend that the two stars are equal
in size.
The authors of Guinan et al., ApJ 509, 21 (1998) acquired a spectrum of the system in the ultraviolet and optical. It shows the light of both stars combined.
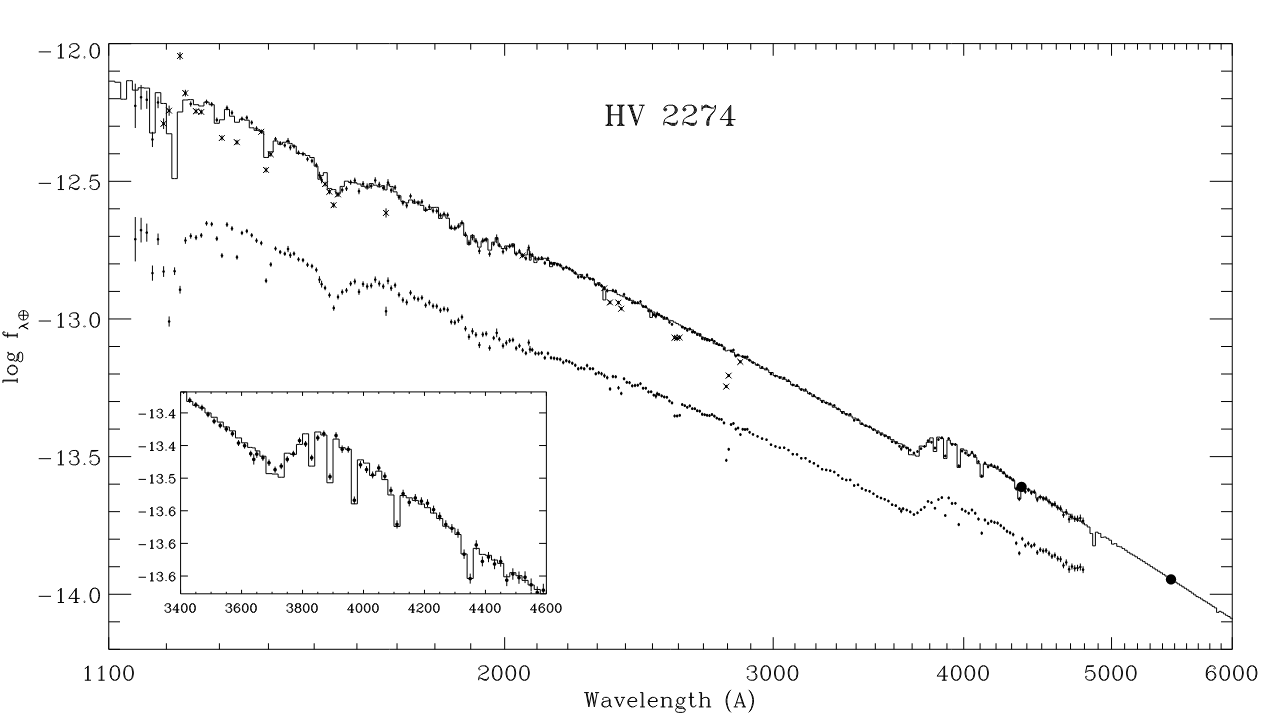
Figure 2 taken from
Guinan et al., ApJ 509, 21 (1998)
Based upon the spectrum, the authors are able to determine the spectral types and effective temperatures of both components. Although they find slightly different temperatures, we can simplify things by treating them as identical. Let's set T = 23000 K.
At this point, we know the following about the stars in HV 2274:
If we treat each star as a perfect blackbody, then we ought to be able to predict the luminosity of each one ... and so the luminosity of both components added together. Remember this?
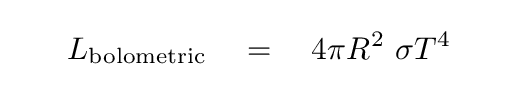
This equation allows us to calculate the total power output of the stars, integrated over all wavelengths. Astronomers call this the bolometric luminosity, to emphasize the fact that it includes radiation over the entire electromagnetic spectrum.
Q: What is the bolometric luminosity of one of the stars in the HV 2274 system? Q: What is the bolometric luminosity of both stars put together?
Okay, so now we have the luminosity of the stars in the HV 2274 system. Our goal is the use this value to determine the distance to the binary. The key is that we can use the Sun as a yardstick: we know the luminosity of the Sun, and we know the distance to the Sun.
Bolometric luminosity of Sun L☉ = 3.83 x 1026 W
Absolute magnitude of Sun M☉ = 4.83
Distance to Sun d☉ = 1.50 x 1011 m
So the inverse square law ought to do the job -- right?
Alas, there is one last tricky item that we must take into account, due to the limited range of wavelengths sampled by our telescopes and cameras. It might be easier to understand if we start the calculation and see what happens.
Since we know the luminosity of both the binary star, and the Sun, we can figure out their difference in magnitudes.
Use this equation to compute a first version of the magnitude difference between the Sun and the HV 2274 system.
Q: What is your first estimate of the absolute magnitude of HV 2274?
But this will give us problems later on. Why? Because the estimate we have just made is based on the blackbody radiation from the HV star system AT ALL WAVELENGTHS. That means our absolute magnitude will be based on light of all wavelengths; in other words, a "bolometric magnitude." Note that the hot object emits lots of light -- most of its light, in fact -- at wavelengths shorter than 400 nm, in the near-ultraviolet portion of the spectrum. At short wavelengths, the hot object emits hundreds or thousands of times as much energy as the cool object (the y-axis has a logarithmic scale).
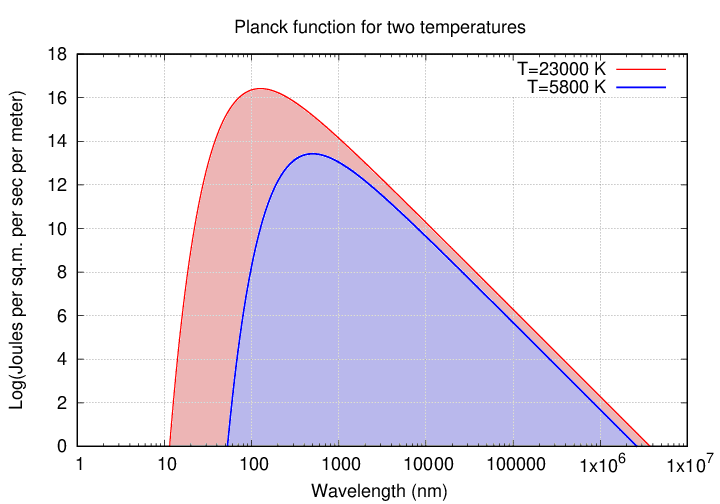
Q: How much more power does the hot star produce at a
wavelength of 100 nm?
The trouble is that the measurements of these stars in the sky were made with an optical telescope, viewing them through a V-band filter. That means that the apparent magnitude is based on a NARROW SLICE OF WAVELENGTHS.
And if you look closely at this narrow range of wavelengths, the hot object does produce more power, yes ... but only by a factor of 30 or 40 -- not hundreds or thousands (again, note the y-axis is logarithmic).
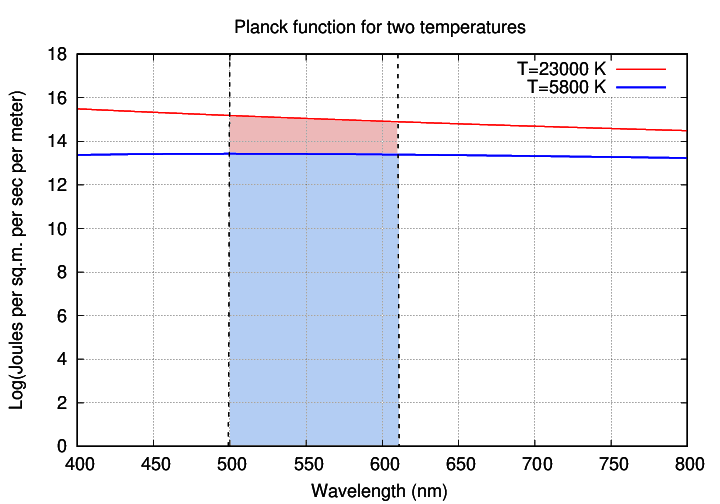
Q: How much more power does the hot star produce at a
wavelength of 550 nm?
So, the optical observations through a V-band filter will show that the hot object is more luminous -- but by a smaller factor than the bolometric calculations would suggest. In order to convert the bolometric magnitude difference into a V-band magnitude difference, we need to include a bolometric correction factor (BC).
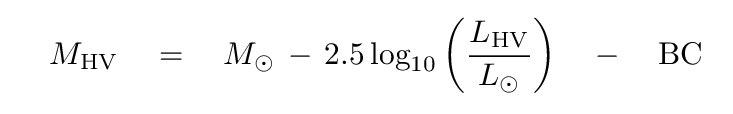
The value of the bolometric correction depends on the temperature of the star, and on the choice of passband. We are using the V-band, which is the most common. It shouldn't be too hard to find a table listing the bolometric correction factors for stars of different temperatures or spectral types; there's one in Appendix E of Carroll and Ostlie, for example.
In our case, for main-sequence stars with effective temperatures around 23000 K, the bolometric correction to V-band is roughly BC = -2.4.
Q: Using a bolometric correction of -2.4, what is the absolute
V-band magnitude of the HV 2274 system?
Q: Use this absolute magnitude, and the apparent magnitude
mV = 14.16, to calculate the distance to HV 2274.
Our calculations have produced a distance to the Large Magellanic Cloud which is a bit larger than the value listed by most studies. Whoops. Have we forgotten some important factor?
Yes. We've neglected to correct for extinction of the light from HV 2274 by clouds of gas and dust lying in the line of sight. According to Guinan et al. (1998), the reddening to the binary has a value of E(B-V) = 0.12. Let's remove the effect of this dust.
The first thing we must do is to convert the reddening E(B-V) (how much does the color of the star change?) into extinction AV (how much fainter does it appear in the V-band?). We can do so by adopting a conversion factor which is usually called "R".
The exact value depends upon the nature of the dust, and can vary from place to place in space, but a typical value is R = 3.1. Once we have the extinction in the V-band, we can compute the intrinsic, dust-free, unextinguished apparent magnitude of HV 2274.
Q: What is the corrected apparent magnitude of HV 2274?
Q: Use this value, and the absolute magnitude, to compute the
distance modulus and distance to the Large Magellanic Cloud.
The authors of this study of HV 2274 derive a distance of 46.8 ± 1.6 kpc to the binary star HV 2274. However, they show evidence that this star lies on the far side of the LMC, a bit farther away than the center of that little galaxy. Correcting for this offset between the binary and the galaxy leads them to a final distance of 45.7 ± 1.6 kpc to the LMC. That's an uncertainty in distance of just about 3 percent!
However, the paper we've just discussed was published in 1998 and involves hot stars, for which stellar models may not be very accurate. More recent papers involving binary star systems in the LMC include:
Both describe binary systems with cooler stars, for which the stellar models are considered more accurate. Pietrzynski et al. (2013) claim that their set of 8 binary systems yields a distance to the LMC barycenter of 50.0 +/- 1.1 kpc, which is not quite consistent with the earlier results.
Elgueta et al. (2016) derive a distance of 49.0 +/- 0.5 (stat) +/- 1.0 (systematic) kpc to the binary OGLE-LMC-ECL-25658, which lies far off to one side of the LMC; once they correct for its location within the little galaxy, they determine a distance to the center of the LMC of 50.30 +/- 0.53 (stat) kpc
Figure 1 taken from
Elgueta et al. (2016).
The binary system OGLE-LMC-ECL-25658
is the red dot to the left of center.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.