
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
In our last meeting, we reviewed the history of several types of peculiar galaxies (or maybe not galaxies) over the course of the twentieth century. We saw that astronomers had identified a number of unusual objects lurking among the "ordinary" galaxies in space.
Thanks to the combined efforts of many scientists, by the nineteen-sixties, some of the quasi-stellar radio sources were recognized as located very, very far away; so far away that they couldn't be stars, but must be some sort of unusually luminous and compact galaxies. The problem was that they were SO luminous and SO compact:
Now, why are these two features -- high luminosity and small size -- a problem? In order to provide a proper answer, we'll need to calculate some numbers.
Q: The Sun has (approximate) absolute magnitude M = +5.
How many times more luminous is a quasar of absolute magnitude M = -25?
Q: The luminosity of the Sun is about L = 4 x 1026 Joules/sec.
What is the luminosity of the quasar?
That's a LOT of power. And based on the sharp variations in brightness of some quasars, the "central engine" must be no more than a light-day across.
Q: How many meters is one light-day?
How can so much power be generated within such a small region?
Black holes are very strange: collections of matter which have been squished to such high density that the gravitational forces at their "surfaces" (event horizons) are so strong that even light cannot escape. If you could fly your ship close to an isolated black hole in space, this is what you would see:

Ho ho.
Of course, if there happened to be a typical celestial backdrop behind it -- hundreds of stars and galaxies shining brightly -- then you might notice something bizarre: although you wouldn't be able to see the black hole itself, you WOULD notice the distortion of light rays passing close to it.

Image and movie courtesy of
OzGrav ARC Centre of Excellence
In order to understand how black holes can power the central engines of active galaxies, we'll need to know their size. The event horizon of a black hole is the surface from which light cannot escape; for many purposes, we can consider that the radius of the object. The radius depends on the mass of the black hole: bigger mass means a larger radius. It's a simple relationship:
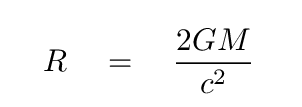
where
For our purposes, it is often useful to describe the mass of a black hole in terms of solar masses. In that case, the equation can be written
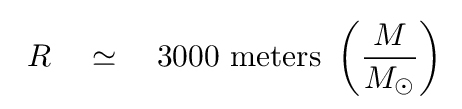
In other words, if the Sun were to turn into a black hole, it would have an event horizon of radius 3 km; and if a star of 10 solar masses were to collapse into a black hole, the resulting event horizon would have a radius of 30 km.
Q: What is the radius of a black hole with 1 million solar masses?
The answer is 3 million km = 3 x 109 meters, of course. This is only about five times as large as our Sun -- while containing one million times as much mass.
Since black holes pack so much mass into so small a volume, they can have rather extreme properties. Consider, for example, the energy an object gains when it falls. For ordinary, everyday situations here on Earth, the calculation is simple.
Q: Suppose that a book of mass m = 1 kg falls from a table
a distance of h = 1 m to the floor.
How much gravitational potential energy is converted into
kinetic energy just before the book lands?
The calculation in space near a black hole is a bit more complex. If an object falls from a very great distance toward a black hole, then just before it enters the event horizon, it will lose this much gravitational potential energy:

where
Consider a supermassive black hole -- one with a mass of M = 1 million solar masses = 2 x 1036 kg. The radius of its event horizon would be R = 3 x 109 meters.
What would happen if we tossed a book of mass m = 1 kg from a distant spaceship and let it fall all the way to the black hole's event horizon? Well, the book would speed up as it fell, converting gravitational potential energy into kinetic energy. How much energy would it gain by the end of its journey?
Q: What is the gravitational potential energy lost as the
book falls to the event horizon?
Express your answer in Joules.
Express your answer in kiloTons of TNT (1 kTon = 4 x 1012 Joules)
For reference, note that the atomic bombs used at the end of World War II had energies of roughly 15-20 kTons.
Well, this looks promising. It certainly seems as if supermassive black holes can convert matter into energy very efficiently. Just how much stuff might we have to drop into a black hole in order to power a quasar?
Given
Quasar luminosity L = 4 x 1038 Joule/sec
Black hole mass M = 1 x 106 solar masses = 2 x 1036 kg
How many kg of matter per second must we drop into the black hole
for the conversion of GPE into KE to match the quasar's luminosity?
Well, that may sound like a lot of matter -- and it IS a lot of matter -- but remember that a typical galaxy has billions and billions of stars, as well as giant clouds of gas and dust. There really shouldn't be any trouble using a supermassive black hole to produce all the power we observe in active galaxies ...
... right?
Well, maybe there is a flaw in the idea of using giant black holes to power active galaxies. If we were to drop objects into the black hole, they WOULD convert gravitational energy into kinetic energy, and they WOULD pick up lots of speed, and they WOULD even be moving at relativistic speeds by the time they reached the event horizon.
The question is, what would happen when they did fly into the event horizon?
Q: What would happen if a small asteroid fell straight into a
supermassive black hole?
The answer is ... NOTHING
The asteroid would just fall into through the event horizon and disappear from sight. All that kinetic energy would just go with it into the black hole and disappear.
No light or X-rays or infrared or radio waves would be produced.
Whoops. That's not going to solve our puzzle of the energy source of active galaxies. We need some way to convert the gravitational potential energy of matter into electromagnetic radiation as it falls into the black hole.
Fortunately, there is a natural solution to this problem. We've been talking about dropping an object from rest straight into a black hole, but in real life, objects will have some motion of their own as they fly through space. As a result, the overwhelming majority of objects will accelerate toward the black hole, but their residual transverse velocity will cause them to miss it and fly past to one side.
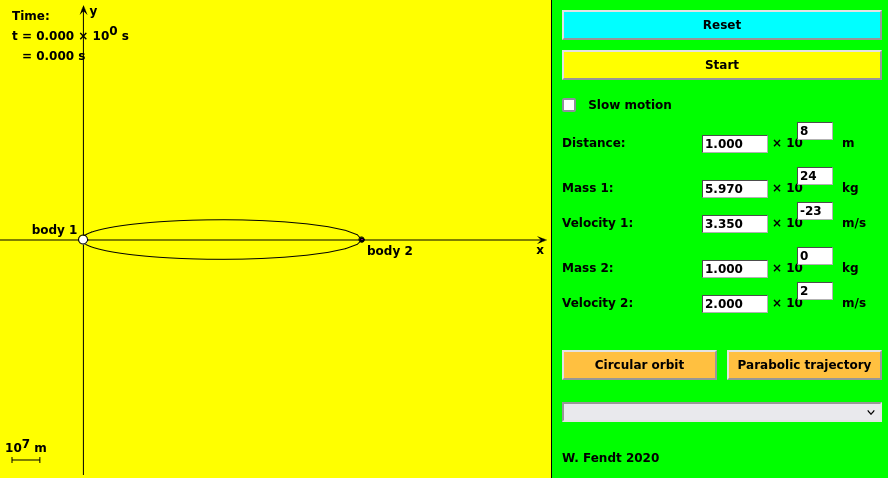
Image and applet thanks to
W. Fendt
However, if a number of objects -- say, atoms in a cloud of gas -- happen to fall past a black hole, the small random motions of the objects will cause them to collide with each other as they fly past it. Those collisions can cause the objects to lose some energy, and some angular momentum. In some cases, the objects will lose so much energy that they can't fly away afterwards, and fall back again and again, each time losing some energy and angular momentum. After a number of encounters, the cloud will form into a flattened disk, and the material will gradually spiral inwards to meet its doom.

Image and animation courtesy of
NASA/Goddard Space Flight Center and Dana Berry (Skyworks Digital)
The reason that the gas doesn't simply orbit in a perfect circle, as the Earth orbits around the Sun, but instead gradually moves inward, is due to the viscosity (something like friction) of gas in the disk. The speed of each atom in its orbit depends on its distance from the black hole: atoms closer to the black hole move more quickly. Consider two atoms in the disk, one slightly closer than the other. The inner atom will move faster, and so catch up to the outer atom as they both circle around. As it passes the outer atom, they may collide, causing them to radiate away a little of their energy and angular momentum; the result will be that the atoms fall inward a small distance.
Over time, the interactions of the atoms in the accretion disk will cause them all to migrate inward, moving closer than closer to the accretion disk. As they move closer, their orbital speed increases, which causes interactions between them to become more violent. These interactions heat the gas: the closer to the center, the more violent the collisions, and so the hotter the gas temperature.
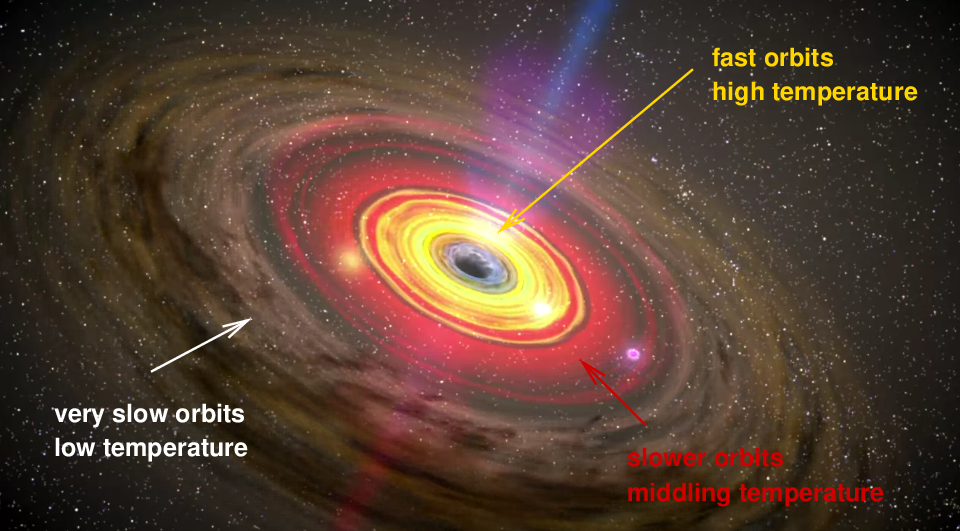
Image modified from
NASA/Goddard Space Flight Center and Dana Berry (Skyworks Digital)
This accretion disk, full of large amounts of gas at a wide range of temperatures, is exactly the mechanism required to convert gravitational potential energy into electromagnetic radiation. Instead of falling quickly and directly into the black hole -- and emitting no light -- the gas very slowly spirals in towards the black hole, heating up as it progresses. As it spirals in, the hot gas emits thermal radiation over a wide range of wavelengths.

Image modified from
NASA/Goddard Space Flight Center and Dana Berry (Skyworks Digital)
Remember the relationship between temperature and peak wavelength of blackbody radiation?
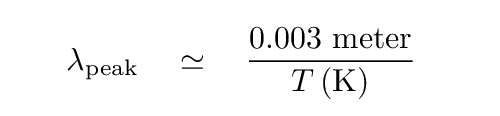
Let's use it to get a very rough idea of the type of electromagnetic radition produced by various portions of the disk.
region temperature (K) peak wavelength (m) spectral region ----------------------------------------------------------------------------- inner disk 30,000,000 middle disk 10,000 outer disk 300 -----------------------------------------------------------------------------
In summary, gas spiraling around a supermassive black hole in a giant accretion disk will produce electromagnetic radiation over a wide range of wavelengths (or frequencies). One can make a model of the emission by breaking the disk up into a series of rings of decreasing temperature, but increasing size. By treating each ring as a separate blackbody, and then adding together the light from all the rings, one can build up an overall spectral energy distribution which spans the range from radio to X-ray.

SED courtesy of
Gulab Dewangan, IUCAA, Pune (India)
That's a nice theory. Do actual active galaxies show similar spectral energy distributions? Yes. Quite a few, actually. (Ignore the emission at very, very high frequencies at far right; that's a story for another day).
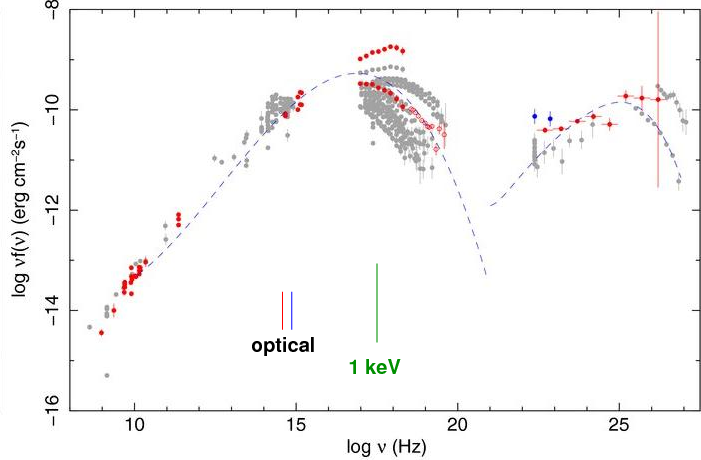
Figure taken from
Abdo et al., ApJ 716, 30 (2010)
So, we believe that at the center of all those active galaxies -- Seyferts and quasars and X-ray-bright objects -- lurks a gigantic black hole with a mass of millions or even billions of solar masses. Surrounding the black hole is an accretion disk of hot gas which emits electromagnetic radiation via the blackbody mechanism, over a very wide range of wavelengths. We call these objects Active Galactic Nuclei, or AGN for short.
Note how this model solves a number of the puzzling observations of peculiar galaxies.
There are some other features of AGN which we don't have time to cover in detail. One of these is the presence of jets in many AGN: narrow beams of electrons and protons shooting out from the poles of the accretion disk at hyper-relativitistic speeds.

Image and animation courtesy of
GoetheUniversitaet
While theorists are still trying to figure out exactly how these jets are produced, observers see them in many AGN, such as M87. It appears in the optical ...

Optical image of M87 courtesy of
NASA, ESA and the Hubble Heritage Team (STScI/AURA); Acknowledgment: P. Cote (Herzberg Institute of Astrophysics) and E. Baltz (Stanford University)
... and at other wavelengths, too.

Images courtesy of
NASA/CXC/MIT/H.Marshall et al. Radio: F. Zhou, F.Owen (NRAO), J.Biretta (STScI) Optical: NASA/STScI/UMBC/E.Perlman et al.
The jets (and the lobes they create when they smash into gas in intergalactic space) are especially prominent in some images created by radio telescopes.

Image courtesy of
NASA, ESA, S. Baum and C. O'Dea (RIT), R. Perley and W. Cotton (NRAO/AUI/NSF), and the Hubble Heritage Team (STScI/AURA)

Image courtesy of
NASA's Goddard Space Flight Center

Radio image of Cyg A courtesy of
NRAO
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.