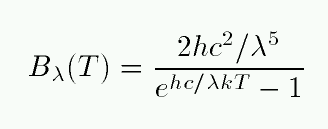
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Astronomers collect electromagnetic radiation across the entire spectrum in their quest to understand stars and galaxies and other objects in space. Before we dive into analyzing the observations of our Milky Way Galaxy, let's review the various physical mechanisms by which celestial objects can produce photons. We'll also look briefly at a few of the techniques we can use to learn more about the sources of the photons we observe.
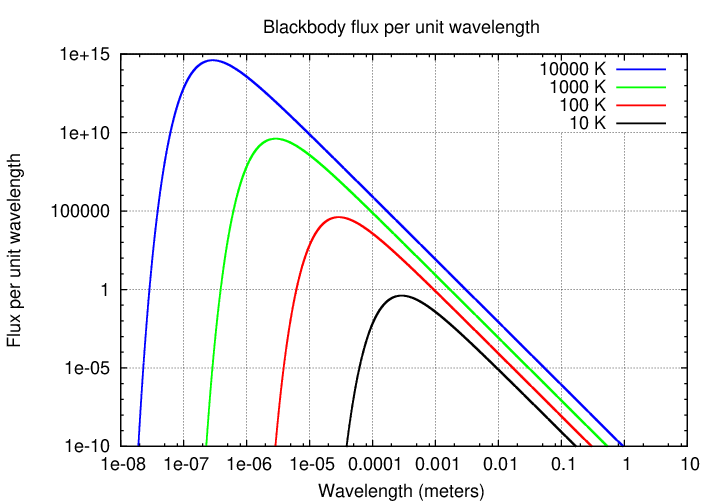
You're familiar with blackbody radiation by now, I hope. These graphs showing radiation as a function of wavelength and frequency should hold no surprises.
Let's start with flux as a function of wavelength λ.
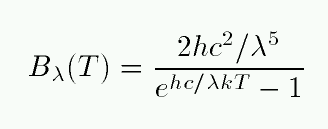
Q: Can you name each of the variables in this equation? Q: Do you know the values of each of the variables?
The flux as a function of frequency ν looks very similar:
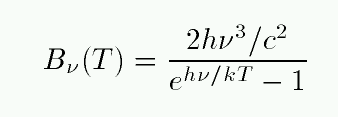
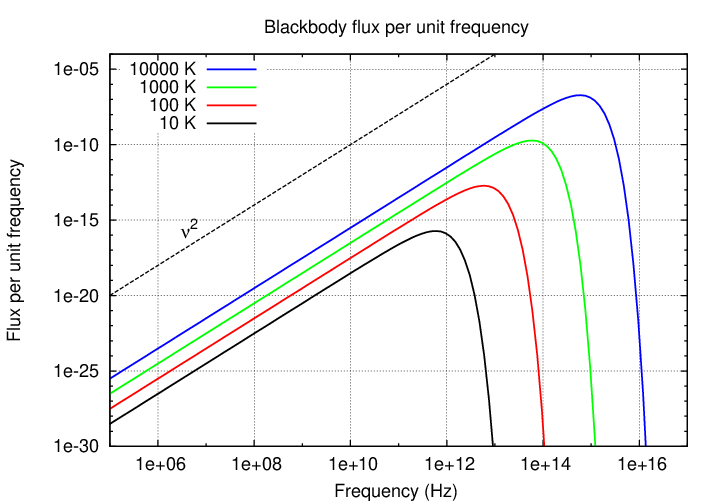
Q: In what portion of this graph would the visible portion
of the spectrum lie? In other words, what is the
frequency of visible light?
Now, we can split the blackbody spectrum into two pieces:
Note that the decrease in flux on the short-wavelength side of the peak is dramatic, due to the exponential nature of the Planck function in that region; but the decrease on the long-wavelength side is much more gradual.
If one measures the slope of the blackbody spectrum on this long-wavelength / low-frequency side of the peak, one finds that, when expressed as flux per unit frequency, it has a slope of exactly 2, as shown in the diagram. Radio astronomers often approximate the spectra of sources by a simple power law, in which the exponent α is called the spectral index.
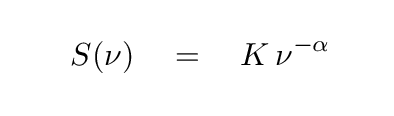
Consider two objects with very different temperatures but similar sizes; say, a white dwarf star (T = 10000 K) and a planet like the Earth, orbiting a sun-like star at the distance of Neptune or so (T = 100 K). Suppose we place these two objects at the same distance from the Earth and observe them.
Q: If we observe in the OPTICAL region, which one is brighter?
By how much?
Q: If we observe in the RADIO region, which one is brighter?
By how much? (look at figure below)
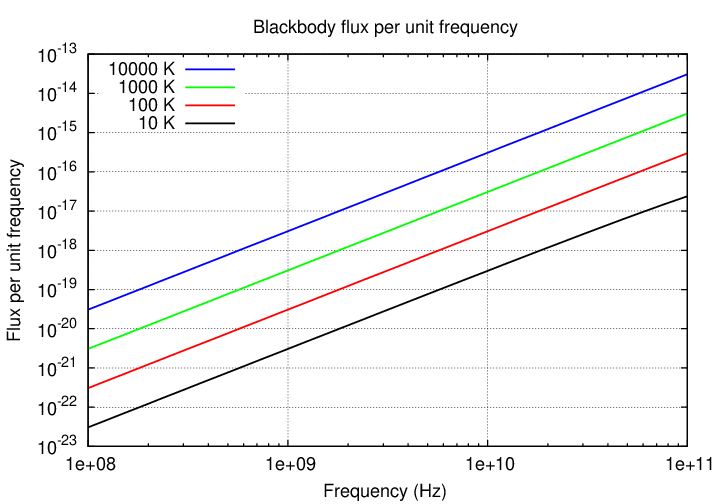
That's one feature of the radio region of the spectrum. Since typical observing wavelengths (longer than 1 mm) are longer than the peak of any object's Planck spectrum, we always observe in the Rayleigh-Jeans tail of the spectrum. And on that tail, objects of different temperatures don't have drastically different fluxes per unit area.
That is one reason that stars -- which are so prominent in the optical sky -- don't show up very much in the radio sky. Sure, they are much hotter than clouds of gas and dust, but that can't make up for their much smaller surface areas.
Note that since objects emit blackbody radiation at all wavelengths, they produce a continuous spectrum; in other words, they are one class of continuum sources. But there are several other classes ...
Another physical mechanism which can produce radiation at all wavelengths involves charged particles trapped along magnetic field lines. When a moving charge encounters a magnetic field, it is accelerated by the Lorentz force
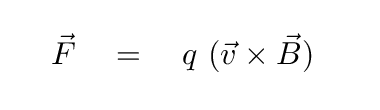
Q: What will happen to the electron as it enters the
region of magnetic field (pointing out of the screen) below?
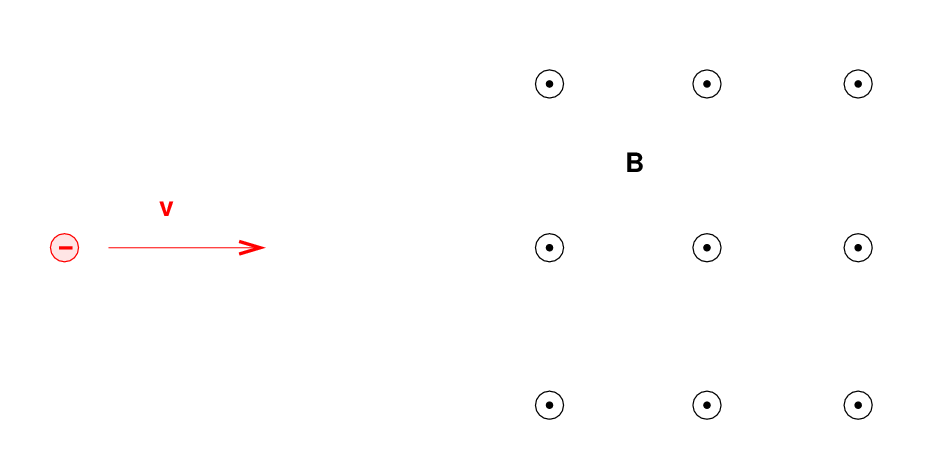
Right. A charged particle will move in a circular path, perpendicular to the magnetic field. But if the particle happens to have some component of its velocity parallel to the field, it will continue to move in that direction with constant speed. The combination of a circle in one plane, plus constant motion perpendicular to that plane, creates a heliacal path.
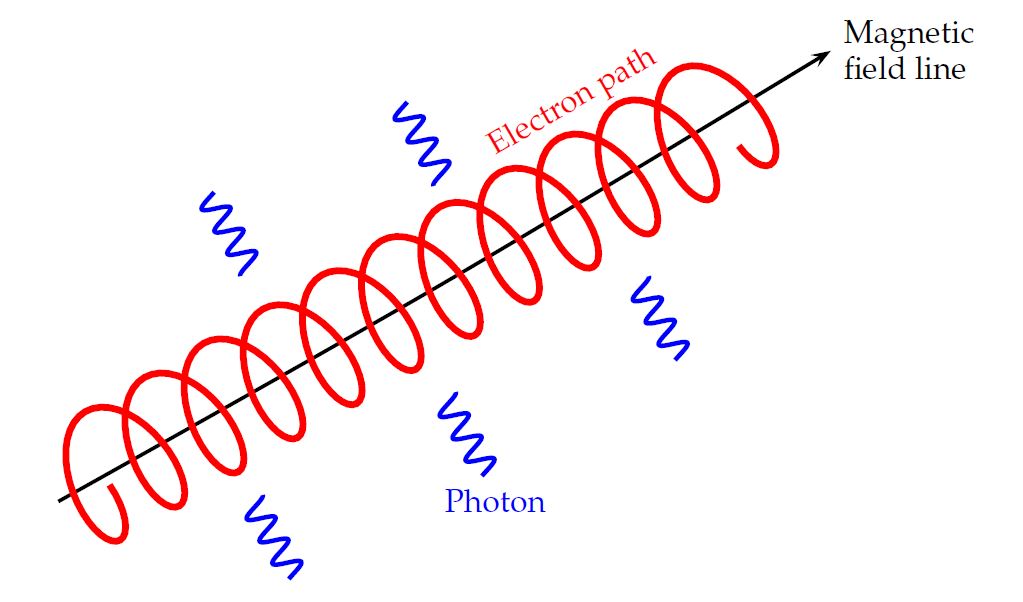
Image courtesy of
Dr. Adrian Jannetta
As the charged particle moves in this path, it is constantly accelerating ... and thus, it constantly emits electromagnetic radiation. The frequency of this radiation depends upon the speed, charge and mass of the particle, the strength of the magnetic field, and the geometry of the motion.
Note that the spectrum of a cloud of ionized gas emitting synchrotron radiation looks very different than a cloud of dense gas (such as a star) emitting blackbody radiation.
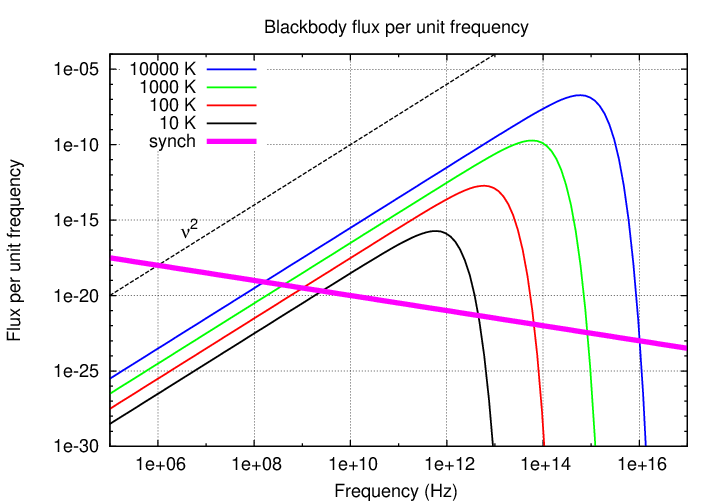
What sort of objects emit primarily via synchrotron radiation? Well, the sort of objects in which lots of ionized gas interacts with strong magnetic fields:
There are MANY examples of synchrotron-bright objects in the Milky Way; for example, the supernova remnant Cas A.
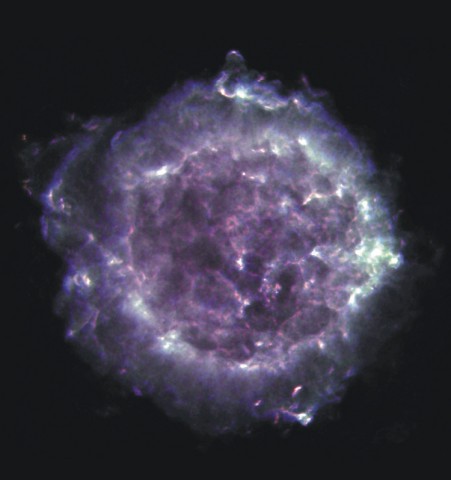
Image courtesy of
NRAO/AUI
Way back in the 1890s, when radioactivity and X rays were both new, exciting phenomena, some physicists noticed that if one shot a high-energy electron into a box of stuff, that it would come out the other end moving more slowly; moreover, the stuff would emit a bunch of X rays.
Because it seemed that there was some connection between the slowing down of the electron and the X-ray emission, physicists gave this phenomenon the name "braking radiation". Since most of those involved in this research were German, the word entered our vocabularies as brehmsstrahlung.
What's happening is the result of close encounters between the energetic electron and positively charged nuclei within the material. If the electron passes very close to a nucleus, the mutual electric force will accelerate the electron strongly; and an accelerating charge emits radiation, as we know from our E&M courses.
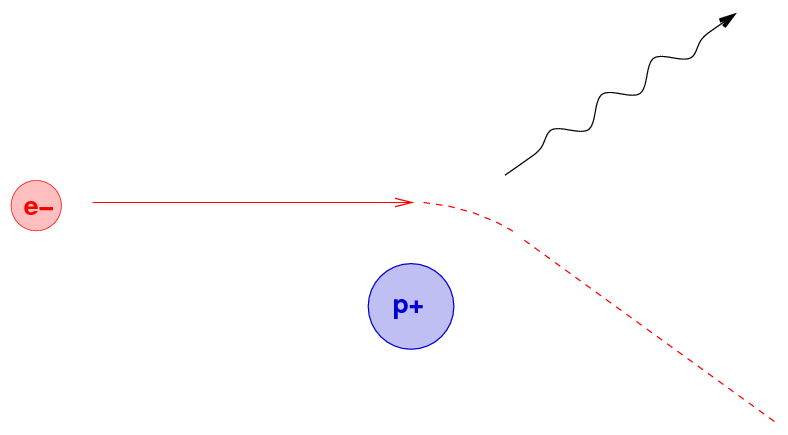
Because the electron might approach the nucleus to within any possible distance, it might end up emitting any wavelength of energy due to a single encounter. As it moves through the material, however, it will interact with numerous nuclei, and so the photons it emits will cover a wide range of energies and wavelengths; in other words, brehmsstrahlung produces a continuous spectrum.
Now, in the 1890s, the source of the energetic electrons was radioactive decay. But out in space, the source of the energetic electrons is often a hot, ionized gas. In that case, the distribution of electron energies is dictated by the temperature of the gas, and so we call the process thermal brehmsstrahlung. In this common case, the emissivity of the gas -- a measure of how much energy it emits per second per unit volume per unit frequency -- can be written as
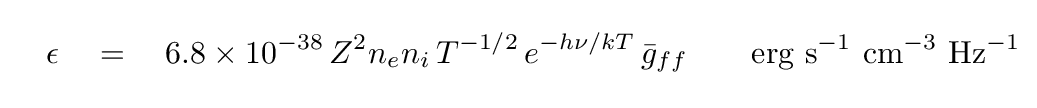
The important features of this emission can be gleaned from the form of the equation.
Q: How does this emission depend on the density of the gas? Q: How does it depend on the temperature of the gas? Q: What happens to the emission at high frequencies?
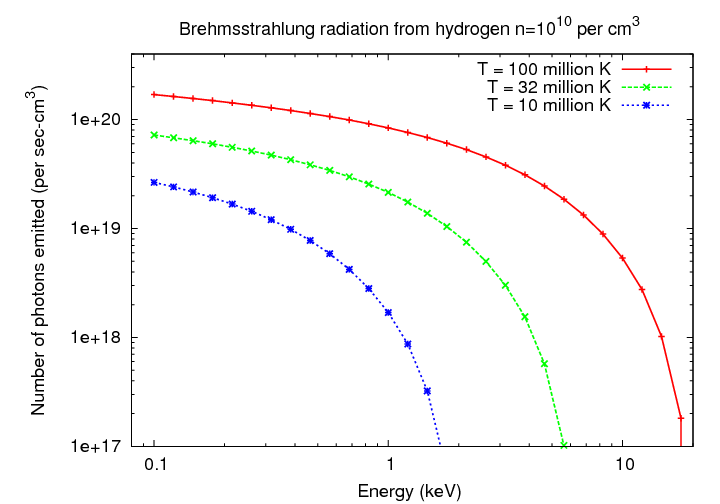
Consider three clouds of (very) hot hydrogen, at tempertures of 10, 32, and 100 million K. Note how the emission in each case effectively cuts off at certain energy, due to the negative exponential term in the equation.
The three mechanisms we've mentioned so far all produce continuum radiation -- photons at all wavelengths and frequencies. But some physical processes in space create lines: either emission or absorption of photons at just one or a few particular wavelengths. As we'll see in a bit, if you can detect lines in the spectrum of an object, you may be able to learn a LOT about it.
The basic idea is that individual atoms, or ions, or molecules, may have a set of discrete energy levels; a fancy way of writing it is that the energy states of these species are "quantized."
Remember the hydrogen atom and its energy levels?
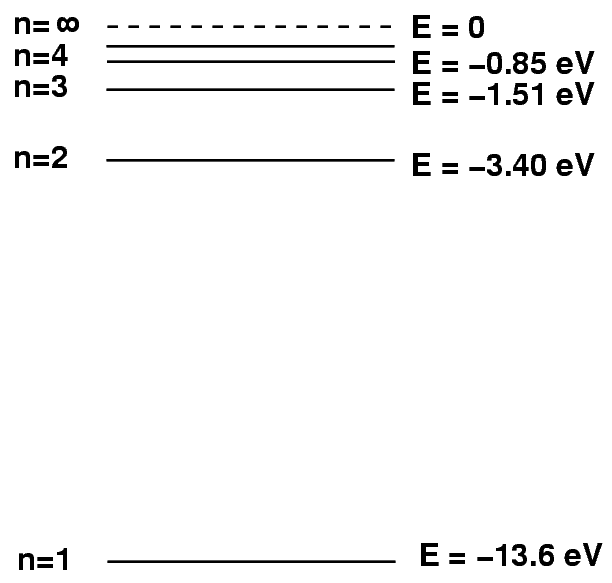
We can write the energy of level n with the following formula:
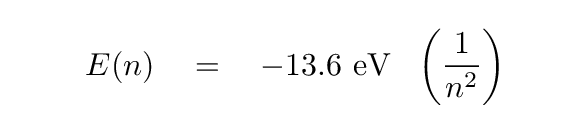
Q: The H-alpha line involves a drop from n=3 to n=2.
What is the energy of this transition, in eV?
What is the wavelength of the photon?
Can you see it?
Q: An astronomer measures a different line, in which
hydrogen atoms drop from n=103 to n=102.
What is the energy of this transition, in eV?
What is the wavelength of the photon?
Can you see it?
There is one very important emission line, which appears in the radio region, which is produced in a somewhat unusual manner. It's very important for the study of the Milky Way, so let's take some time to focus on it.
This particular line doesn't involve the transition between ordinary electronic energy levels, or rotations or vibrations of molecules; instead, it is the spin-flip or 21-cm transition of isolated neutral hydrogen atoms.
The mechanism involves the spin magnetic moments of the proton and the electron within a single atom. It turns out that these magnetic moments can be parallel (pointing in the same direction) or anti-parallel (pointing in opposite directions). The anti-parallel arrangement has a slightly lower energy.
Now, occasionally, a hydrogen atom in this lower-energy state might bump into another atom. If the conditions are right, the atom might gain enough energy in the collision to jump into the parallel-spin, higher-energy state.
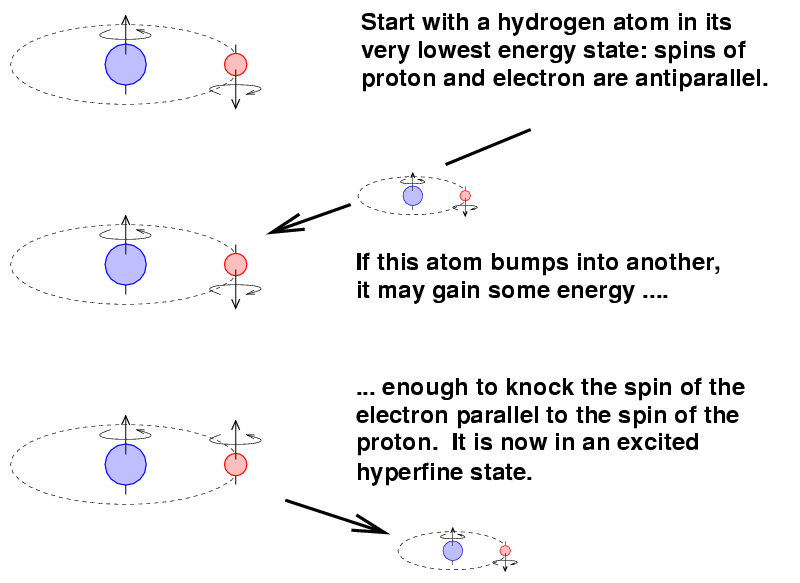
The transition from this excited state back to the ground state is ... not a quick one. On average, it takes around ten million years for an atom to make the change.
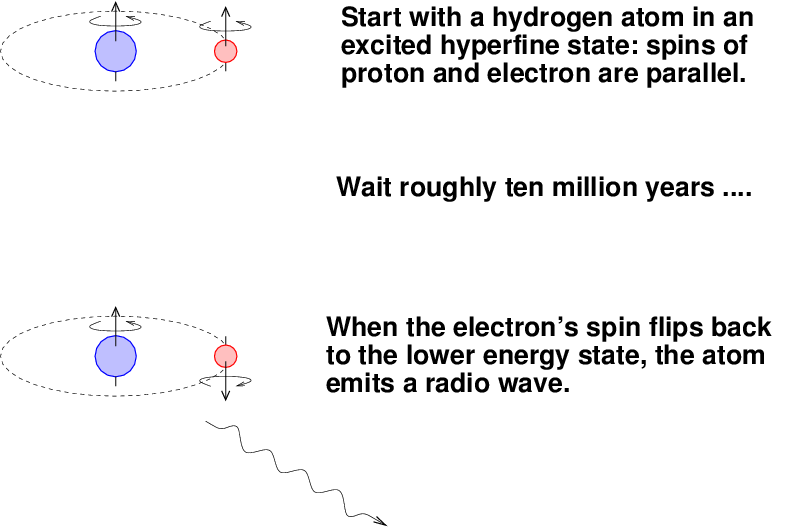
Q: What does that tell you about the atoms in the clouds
which emit this gas?
The difference in energy between the two states is very, very small:
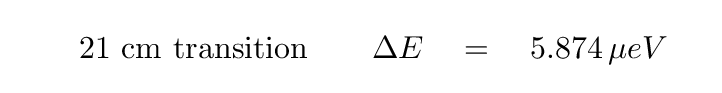
The wavelength of the transition is about 21.1 cm, and the frequency about 1420 MHz. You may recognize that frequency from radio searches for extraterrestrial civilizations; it sits at one end of the so-called "Water Hole."
Okay, fine, so there's a special transition involving hydrogen atoms. So what?
This is a really, really useful line because
That means that it is great for detecting the majority of gas in most galaxies, and revealing its motions. In many cases, the clouds are optically thin to this radiation, which means we can see all the gas and estimate its mass.
Compare the view of the plane of the Milky Way in the optical, in CO emission (showing molecular hydrogen clouds), and in 21-cm emission (showing atomic hydrogen clouds):

Images courtesy of
NASA's 'The Multiwavelength Milky Way'
Because the photons created in a line emission (or absorption) process have discrete energies and wavelengths and frequencies -- which we can measure VERY precisely in labs here on Earth, or predict via theoretical physics -- they can sometimes provide us with information that continuum sources cannot.
For example, suppose that radio astronomers measure emission from a cloud of gas not at the expected wavelength of λ0 = 21.106 cm, but instead at a slightly longer wavelength of λ = 21.109 cm.
Q: Why might the wavelength be slightly longer? Q: What can you deduce about that cloud of hydrogen?
One application of HI observations provides astronomers with a method to estimate the rotation speeds of spiral galaxies, based on the width of their HI emission lines (which, in turn, can help us to estimate their mass). Such HI measurements are the basis for a very powerful technique called
Using radio telescopes with high spatial resolution, astronomers can measure the velocities of gas in nearby galaxies to produce spatially resolved maps of gas motions. Our nearest big neighbor, M31, looks like this:
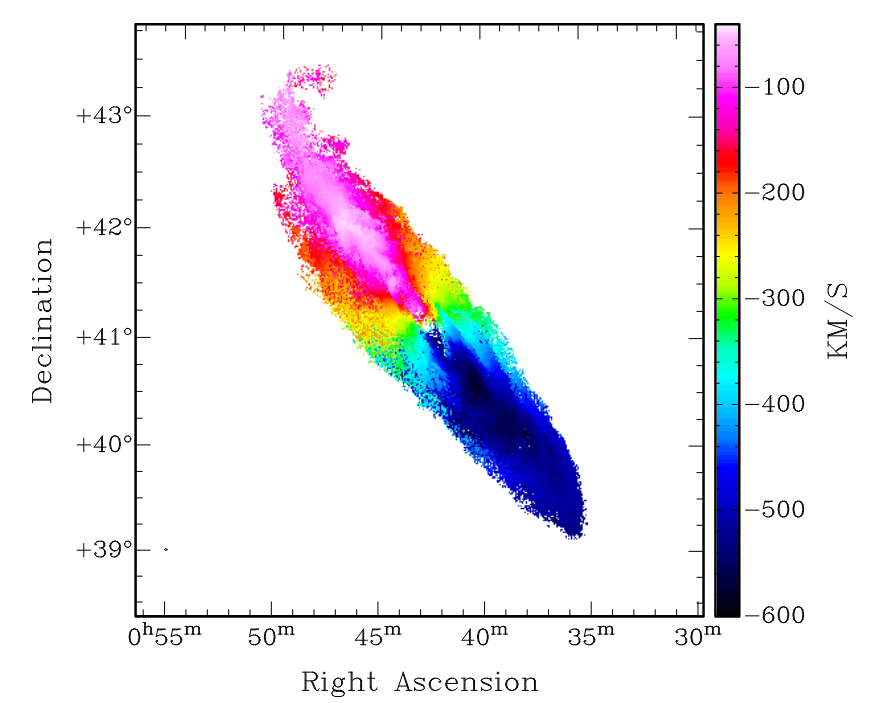
Figure 8 taken from
Chemin et al., arXiv 0909.3846 (2009)
Q: What is the average speed of M31 relative to the Earth?
Is it moving toward us, or away from us?
Q: What is (roughly) the speed with which gas in the disk
of M31 is rotating around its center?
These maps can be analyzed to yield very precise rotation curves of galaxies.
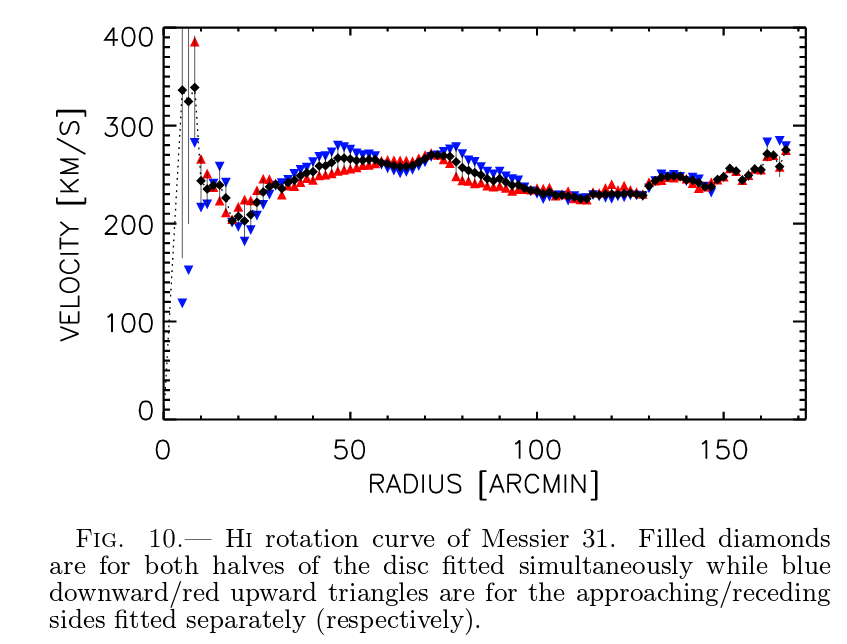
Figure 10 taken from
Chemin et al., arXiv 0909.3846 (2009)
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.