 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Back in the nineteen-seventies, astronomers first gained strong evidence for quantitative relationships between certain properties of galaxies. The important point is that certain features which are independent of distance can tell you something about other features which are dependent on distance -- such as the luminosity or mass.
We'll look at two of the papers which gave this field a kickstart. There has been a great deal of additional research done with each idea in the past decades, of course.
The key point of the Tully-Fisher relationship is that the speed of rotation of material in a spiral galaxy is related to the luminosity of that galaxy: high speeds occur in galaxies of high luminosity.
To establish this fact, TF77 carefully selected galaxies for which rotation velocities could be measured accurately. They used radio telescopes tuned to the 21-cm line of neutral hydrogen, which is plentiful in the disks of many spirals. Gas is a very convenient tracer of dynamics because -- in ordinary spirals, at least -- it orbits the center of the galaxy in circular paths.
If one points a single-dish radio telescope at a typical galaxy -- as TF77 did -- the beam of the telescope is so large that it captures radio waves from the entire galaxy in a single pointing.

The radio image produced by an observation like this is bland: just a single unresolved blob of emission. However, one can easily measure the intensity of the radio waves at different frequencies, which corresponds to the amount of emission at different velocities within the galaxy. Here are eight examples from TF77, showing the measured radio intensity as a function of velocity.
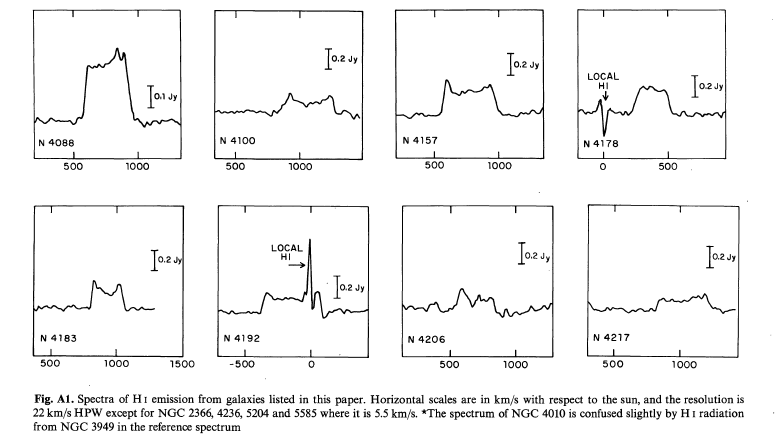
The measured width of the HI line needs to be corrected for the inclination of the galaxy: the more edge-on the galaxy, the smaller the correction. TF77 selected only galaxies with an inclination angle of at least 45 degrees, in order to minimize errors caused by this inclination correction. Notice the light tension here:
To calibrate their relationship, TF77 chose a set of galaxies which were close enough that astronomers had decent measurements of their distances; and, therefore, their luminosities (or absolute magnitudes). Unfortunately, this set didn't have very many high-luminosity systems. In order to test the relationship on high-luminosity systems, they observed galaxies in two nearby clusters, Virgo and Ursa Major. They didn't know the distance to those galaxies, but they could -- with some effort, as they describe in the paper -- find samples of objects which ought to be at the same distance, so that the apparent magnitudes would differ from the absolute magnitudes by a fixed offset.
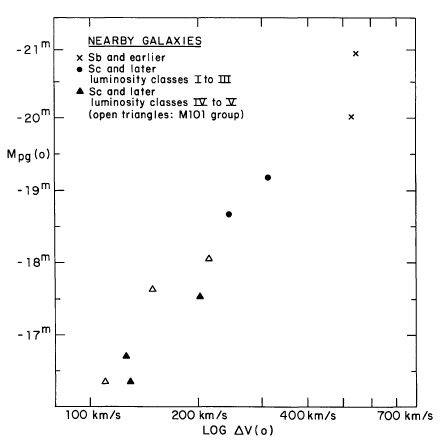
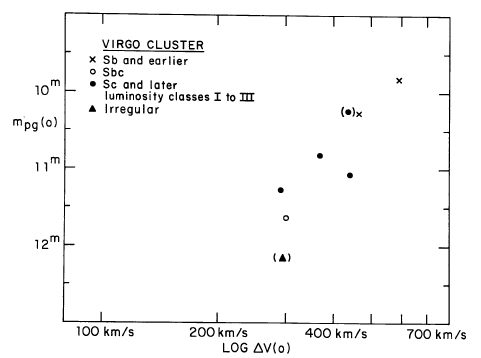
Now, the first question was -- is there a similar connection between rotational velocity and absolute magnitude for both groups of galaxies? Take a look for yourself in the figures above. TF77 concluded there was.
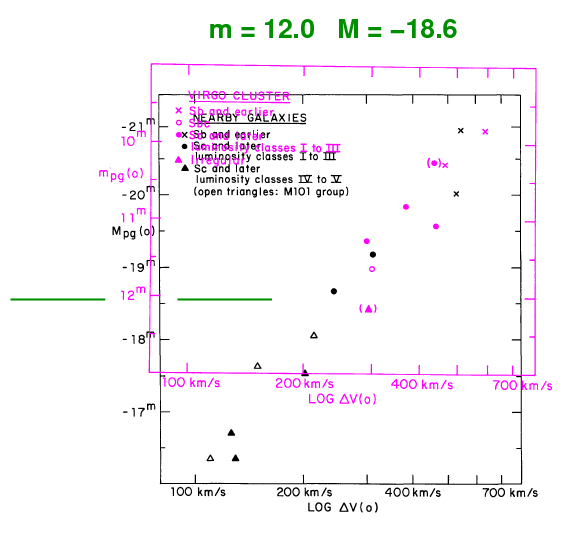
The second question was -- how can we USE this relationship? Well, if the connection is the same for all spiral galaxies, everywhere, then we should be able to determine the distance modulus (m - M) by simply sliding the data for the Virgo cluster galaxies until they line up with the results for galaxies with known absolute magnitudes.
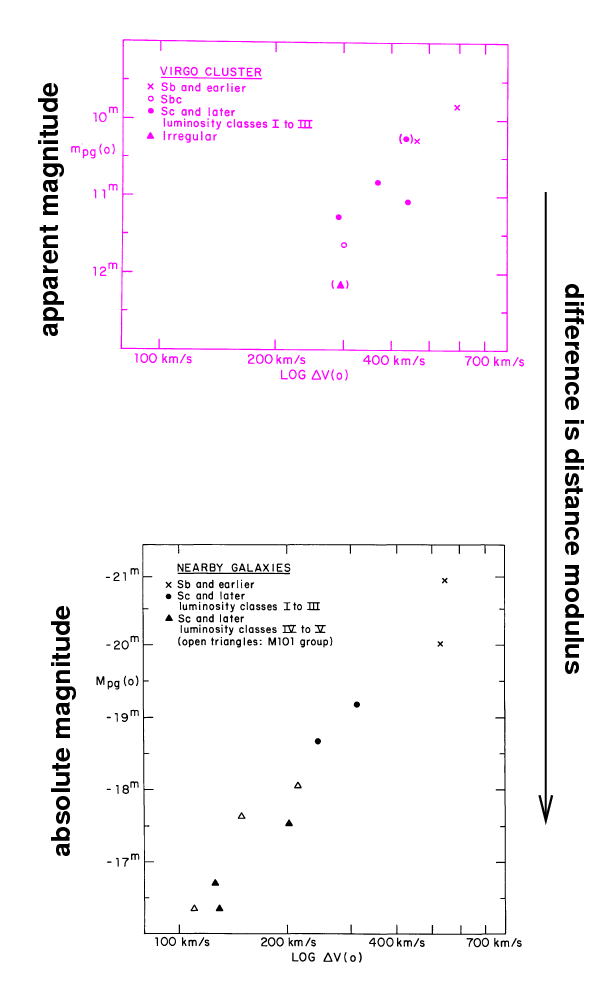

A brief digression on the "luminosity class" of a galaxyTF77 mention the "luminosity class" of some galaxies in their sample. This isn't related to the luminosity class of the stars in them, but refers to a second criterion for separating galaxies -- one beyond the usual spiral/elliptical dimension.
The term was first defined by van den Bergh ApJ 131, 215 (1960):

Below are the 6 Sc galaxies originally chosen to define luminosity classes I - V.
Class I: NGC 4321 = M100.

Image courtesy of ESO/HAWK-I and P. Grosbel.Class II: NGC 3184.

Image courtesy of Al Kelly and Arne Henden.Class III: NGC 2403.

Image courtesy of Subaru Telescope, National Astronomical Observatory of Japan (NAOJ)Class IV: NGC 247.

Class IV-V: NGC 45.

Image courtesy of Rob GendlerClass V: DDO 122 = UGC 7490.

Image courtesy of Dale et al. 2009 and Spitzer Local Volume Legacy Survey
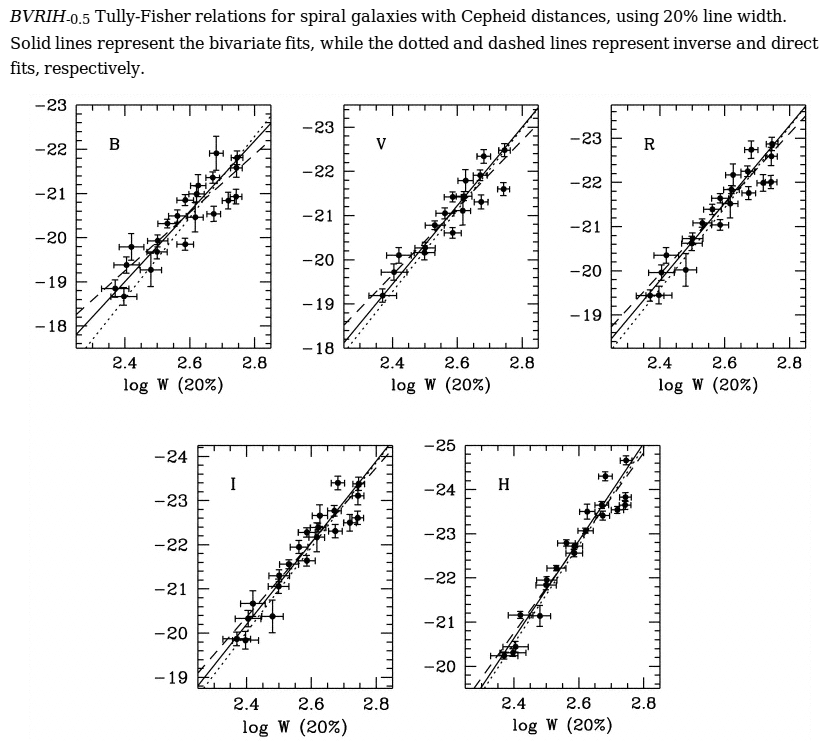
A good summary of recent work on the Tully-Fisher relationship can be found in Sakai et al. ApJ 529, 698 (2000) . The authors test the connection between HI velocity and luminosity in several different passbands, rather than the single bluish photographic passband of the earlier work. They find that the relationship grows tighter if one measures luminosity in the near-IR:
Note that TF77 found that the distance modulus to the Virgo cluster was (m - M) = 30.6 mag, or 13.2 +/- 1 Mpc; that agreed with the "short" value of the time, as opposed to the "long" value of (m - M) = 31.45 mag proposed by Sandage and Tamman. More recent work, such as Mei et al. ApJ 655, 144 (2007), finds a value somewhere in between, but closer to the "short" scale: (m - M) = 31.1 mag, or 16.5 Mpc. TF77 found the distance modulus to the Ursa Major cluster was (m - M) = 30.5 +/- 0.35 mag, or 12.6 +/- 2 Mpc. This is again a bit smaller than more recent values of (m - M) = 31.3 mag (Tully and Pierce ApJ 533, 744, 2000) or (m - M) = 31.6 mag (Watanabe et al. ApJ 555, 215, 2001).
Most elliptical galaxies do not have a significant rotation; that is, the motions of the stars within them show little evidence for a common direction. However, in some galaxies, the stars move very quickly in their orbits -- these tend to be the massive ones -- and in others, the stars move relatively slowly. One way to quantify the motions of stars in such systems is by the dispersion of their velocities: mathematically speaking, if we could measure the radial velocities vi of N individual stars i in a galaxy (which we can't, in almost all cases), the velocity dispersion σ could be calculated as
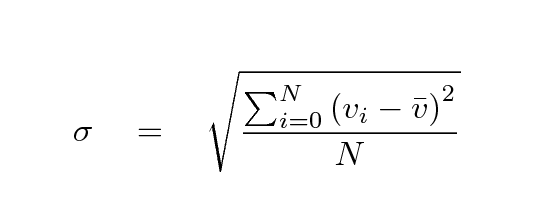
where ![]() is the average velocity.
is the average velocity.
In most galaxies, we can't distinguish individual stars. When we take a spectrum, the light of many, many stars is all mixed up, yielding a composite spectrum of the entire population. Since some of the stars are moving towards us, and others away from us, while some have no radial velocity at all, features in the composite spectrum are smeared out in wavelength space. The larger the range of motions, the larger the degree of smearing.
Consider this single K3 III star, at rest with respect to the Earth. The spectrum is taken from STELIB via Vizier.
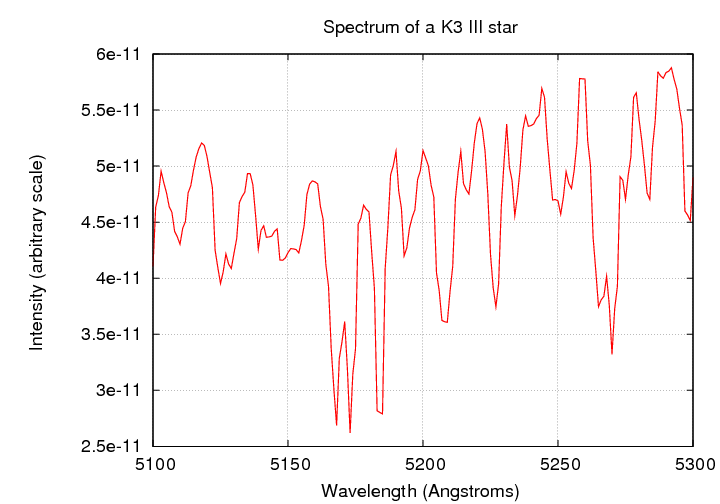
If an identical star moves away from us at a speed of 100 km/s, its spectrum will be shifted to longer wavelengths.
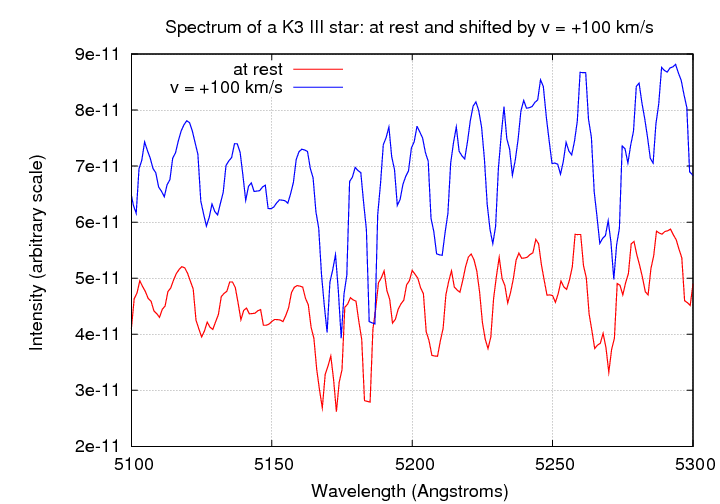
If the light from those two stars is mixed together, the result is a spectrum in which the features are slightly diluted.
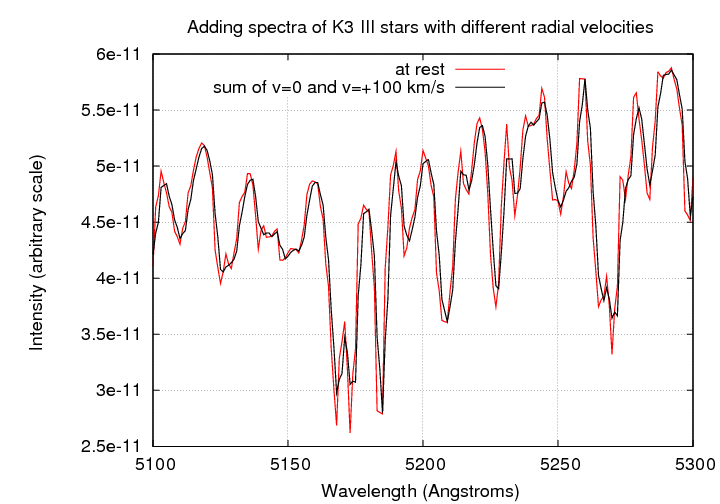
If a system contains stars with a wide range of velocities ...
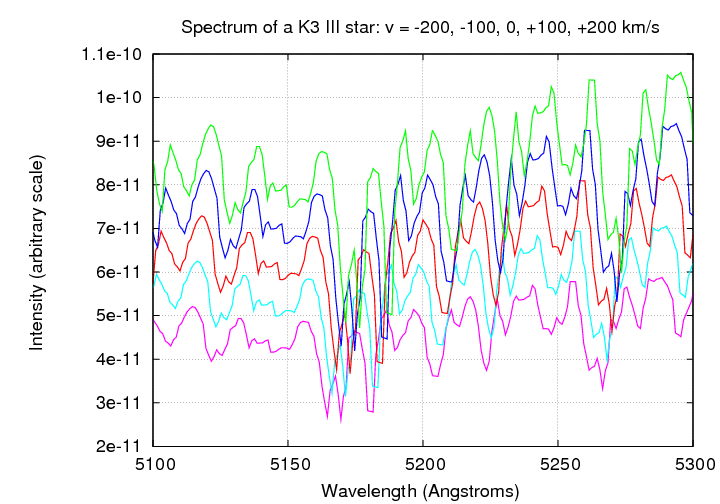
... then the integrated spectrum will look smeared out compared to the original.
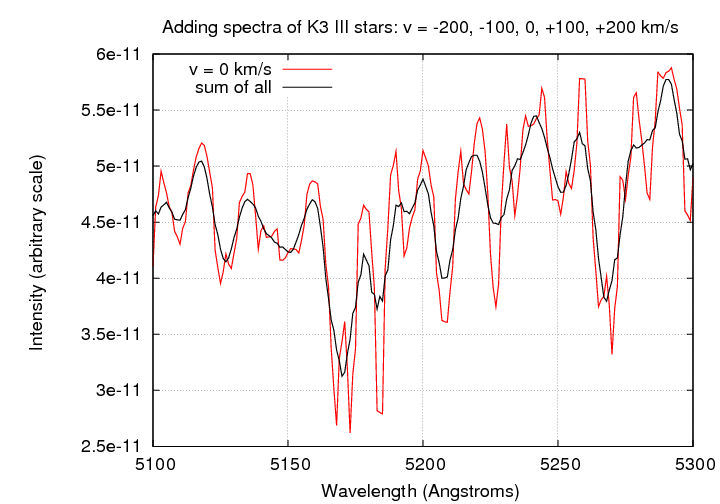
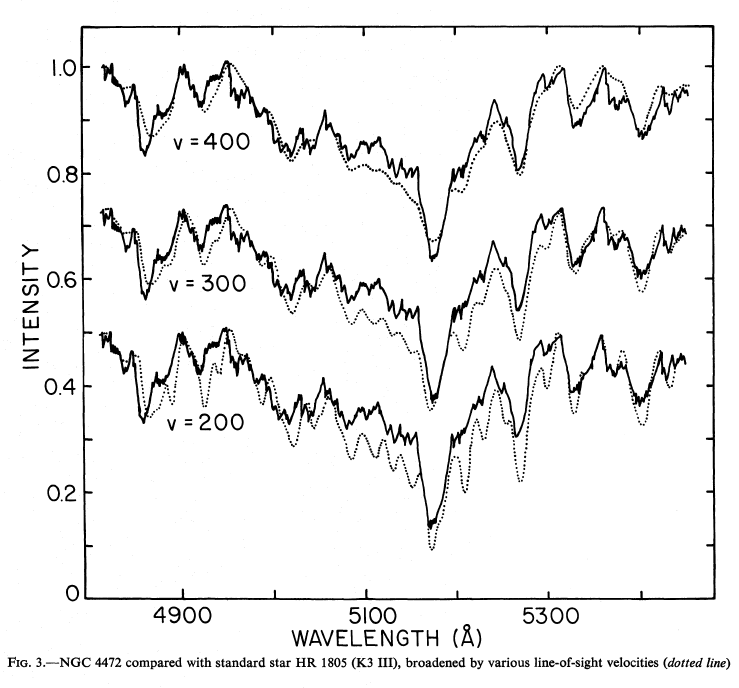
Faber and Jackson measured the velocity dispersion in their sample of elliptical galaxies by comparing the spectrum of light from the center of each galaxy to a series of synthetic spectra, in which a single template spectrum was broadened in a series of steps:
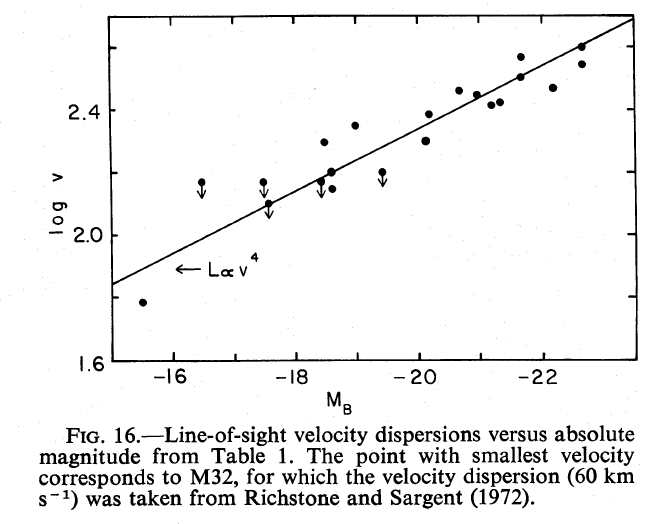
When they compared the velocity dispersion of each galaxy to the absolute magnitude of the galaxy, they found a pretty good correlation: galaxies with large velocity dispersions tend to be more luminous.
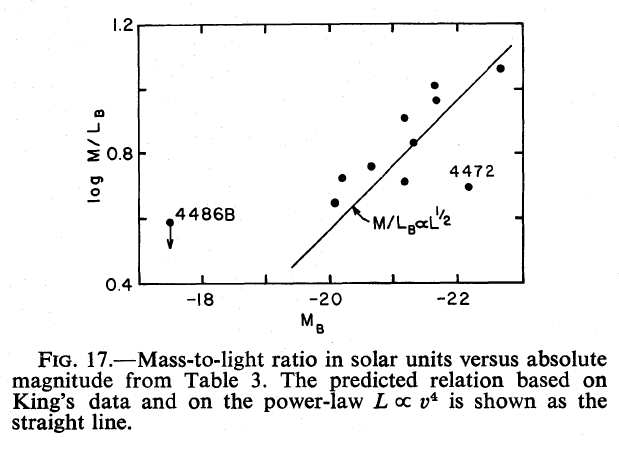
Another connection can be made between velocity dispersion and mass-to-light ratio: galaxies with high velocity dispersions also have high mass-to-light ratios. Since velocity dispersion is correlated with absolute magnitude, this means that mass-to-light ratio is also correlated with absolute magnitude.
So, let's summarize the findings of FJ76: elliptical galaxies (*) appear to be a family of objects which are vary in a systematic way, in a function of a single parameter.
low mass high mass <------------------------------------------------------> low luminosity high luminosity small sigma large sigma low mass-to-light high mass-to-light small size large size <------------------------------------------------------>
(*) aside from dwarf ellipticals
In the years since FJ76, astronomers have accumulated many more observations of elliptical galaxies. We confirm that there is some close connection between several fundamental properties of ordinary elliptical galaxies.
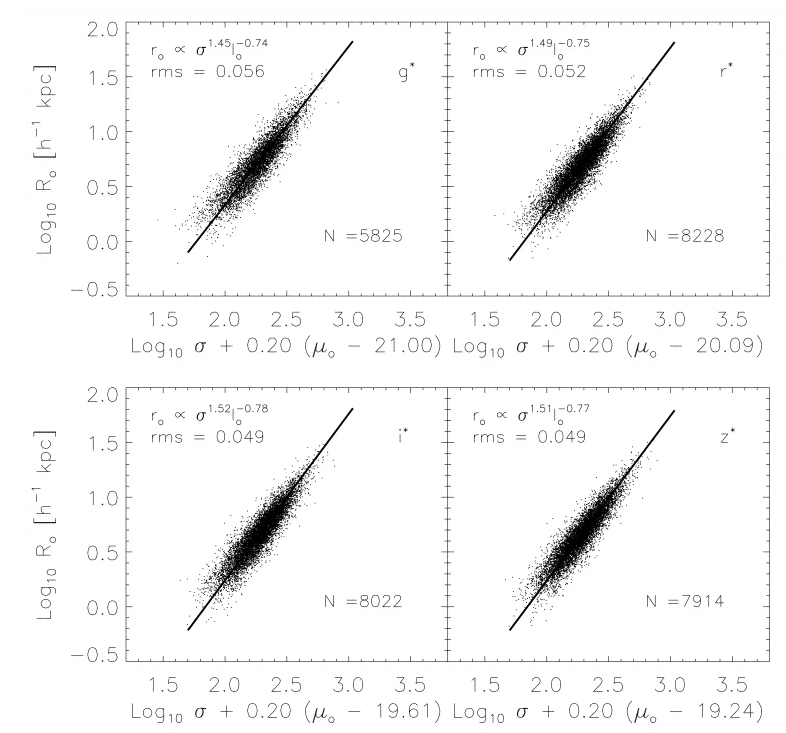
FJ76 discussed the first two properties: luminosity and velocity dispersion. Sometimes, astronomers pick size -- denoted by the term Dn, which stands for "diameter measured at a particular level of surface brightness" (20.75 mag per square arcsecond in the case of Dressler et al., ApJ 313, 42 (1987) -- and velocity dispersion as the quantities of interest. In this case, you might see the Dn-σ relationship.
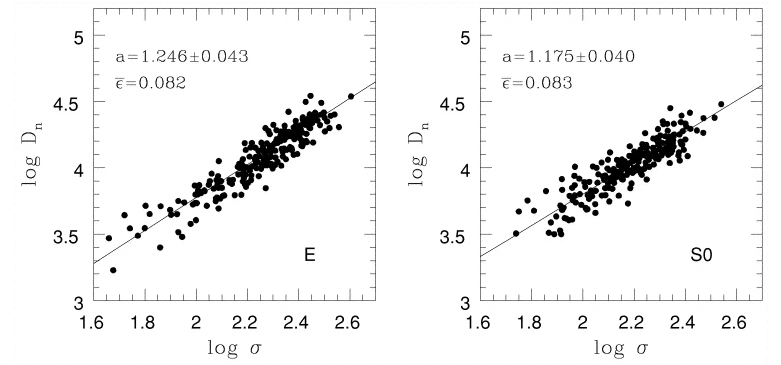
Figure taken from
Bernardi et al., AJ 123, 2159 (2002)
Let's go back to FJ76, which discussed luminosity and velocity dispersion. The top-left panel from this figure Diaz and Muriel, MNRAS 364, 1299 (2005) shows a more recent version of this relationship. It's obvious, but note that there is quite a bit of scatter around the trend. The relationship looks a little bit tighter if one plots luminosity as a function of size, as shown in the panel at top right.
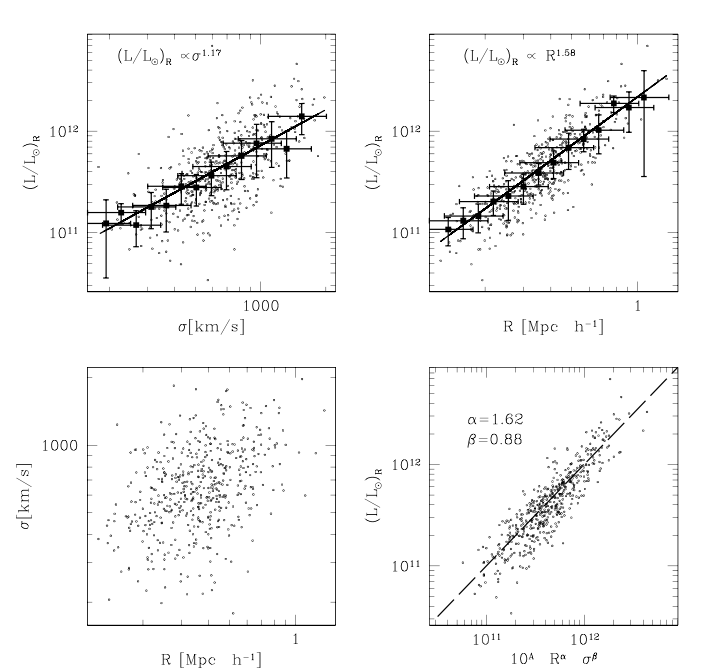
Now, the bottom-left panel shows a rather weak dependence between velocity dispersion and radius: big galaxies have high velocity dispersions. But there might be some sort of systematic skewing: maybe the connection between radius and velocity dispersion does run exactly along the same lines as the connection between radius and luminosity. In that case, we could improve the quality of the relationship by throwing all three quantities into a big blender -- if we mix them up in JUST the right proportion, we can find a model which matches the observations better than the simple one. Look at the bottom-right panel in the figure above.
Because there are three variables, not just two, people describe this relationship among the properties of elliptical galaxies as the fundamental plane (the term was coined by Djorgovski and Davis in 1987). The idea is that we can use any two of the three quantities to predict the value of the third, in some manner equivalent to:
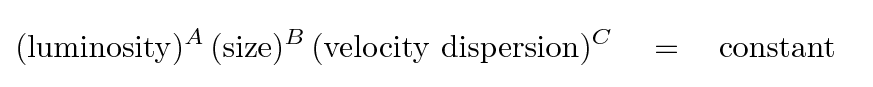
There are many different ways that one can express this idea, given that each quantity can be described in several different ways, and on scales with may be linear or logarithmic. For example, La Barbera et al., ApJ 689, 913 (2008) choose to use normalized values of velocity dispersion, effective radius and surface brightness within the effective radius.
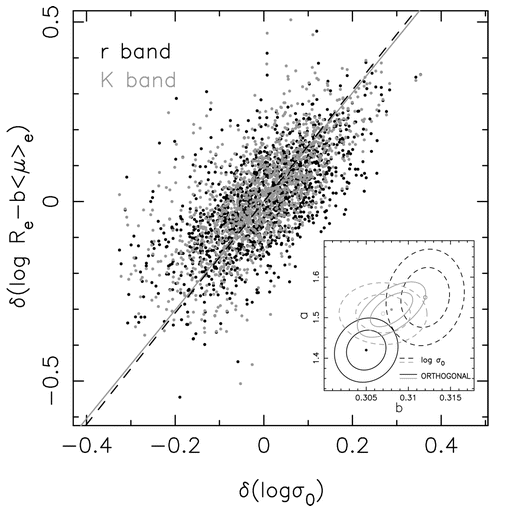
Bernardi et al,, AJ 125, 1866 (2003) use the same variables, but their notation is a little different. Note that the connection between dynamics, luminosity, and size is seen in passbands across the optical.
Okay, so we observe that luminous spiral galaxies have a large range of HI velocities. Is that some random correlation, or does it reflect some deeper physical meaning? If so, what?
Well, it DOES reflect some deeper physical meaning, and a pretty basic one at that. If some group of objects forms a gravitationally bound system in equilibrium, then the virial theorem tells us that the kinetic and potential energies of the bodies must be related like so:
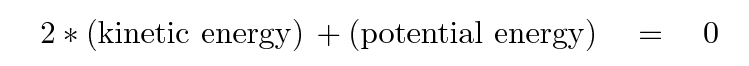
Mathematicians can be express this idea in a more compact way:
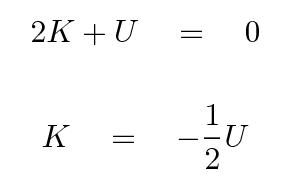
Consider a very, VERY simple model of a spiral galaxy: a big mass M at the center, around which a small clump of gas with mass m moves in a circular orbit of radius R. One might call this a Keplerian spiral galaxy ... In this model, the gravitational potential energy and kinetic energy are
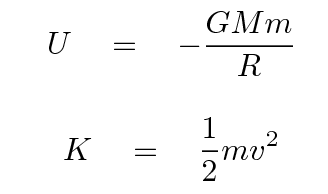
What happens if we solve for the velocity of the gas?
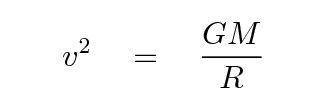
Now, in this simple toy model, suppose that the mass-to-light ratio of the system is some fixed value for all spiral galaxies; perhaps that means that they have similar stellar populations. If that were true, then we could rewrite the relationship as
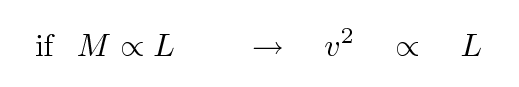
Voila! This is exactly what TF77 found.
What about the Faber-Jackson relationship? Let's consider the simple version first, as discussed in the original paper: observations indicate that the velocity dispersion and absolute magnitude are related in a particular manner. Let's begin with the virial theorem again, since elliptical galaxies are presumably in some dynamical equilibrium. It is possible to show that, even when the distribution of mass is more complicated than the Keplerian case, the velocity dispersion of stars will have a similar connection to the total mass and radius of the system:
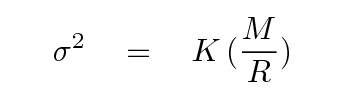
Now, let's again assume that the mass-to-light ratio is roughly the same for all systems, so that we can again replace M with L.
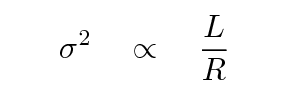
At this point, we must make another assumption: suppose that the surface brightness of galaxies is also a constant. Now, this is obviously not true in reality, but for ordinary ellipticals, it's not an egregiously incorrect statement. If we make this assumption, then we can a mathematical connection between luminosity and radius:
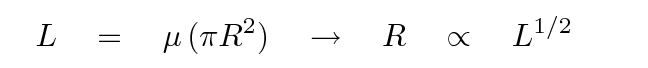
Q: Put the previous two equations together,
and solve for luminosity in terms of
the velocity dispersion.
What do you find?
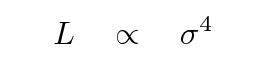
Look again at Figure 16 from TF77:

Ta-da!
Of course, we over-simplified in the derivation above: all elliptical galaxies do NOT have the same average surface brightness, or central surface brightness. The giant, luminous galaxies have a somewhat lower central surface brightness than the smallish ones. See, for example, results from Kormendy et al., ApJS 182, 216 (2009) , which show measurements of galaxies in our own Local Group and in the Virgo cluster. Ignore the green points -- the spheroidals -- for the moment, and just look at the "ordinary" ellipticals, which are shown as blue and red circles.
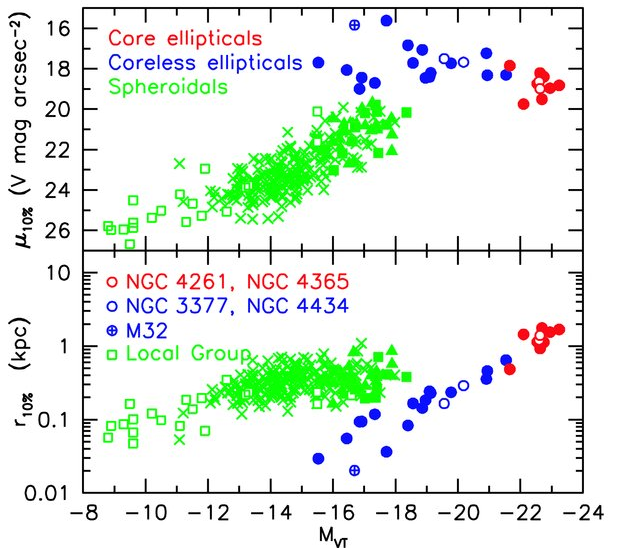
It is due to the additional, complicating relationships between surface brightness and size that we can reduce the scatter in our model by moving from a "fundamental line" in a log-log plot to a "fundamental plane."
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.