Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Just how can one figure out the amount of mass in a galaxy from the motions of objects within it? That sounds pretty complicated. Let's start with a simple situation in order to see the basic idea.
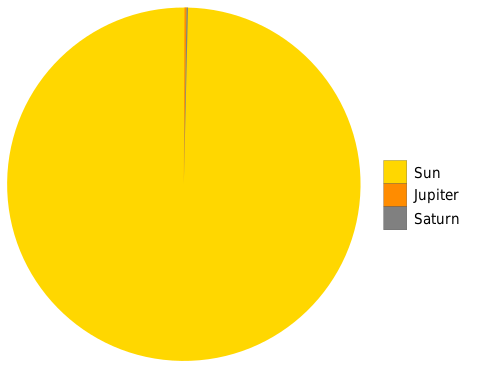
Our Solar System consists of
In this case, almost all the mass resides in one object, the Sun, which sits at the center of the system.
Graph courtesy of
Das steinerne Herz and Wikimedia
For our purposes, we can ignore all the gravitational interactions which don't involve the Sun. That means that the motion of every planet is very simple, due only to the gravitational force of the Sun.
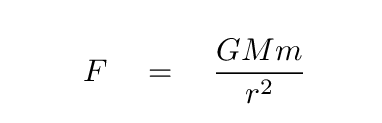
For objects in circular orbits, we can equate the centripetal force on the object to the gravitational force from the Sun.
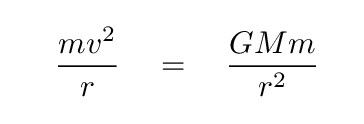
Q: Can you solve this equation for the velocity as a function
of radius?
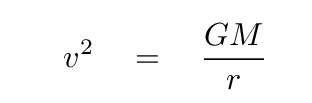
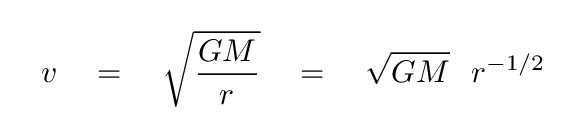
When we measure the speeds of planets and asteroids in our Solar System, we find exactly this sort of relationship. It is often called "Keplerian motion", as it is consistent with the rules Johannes Kepler described in his work.
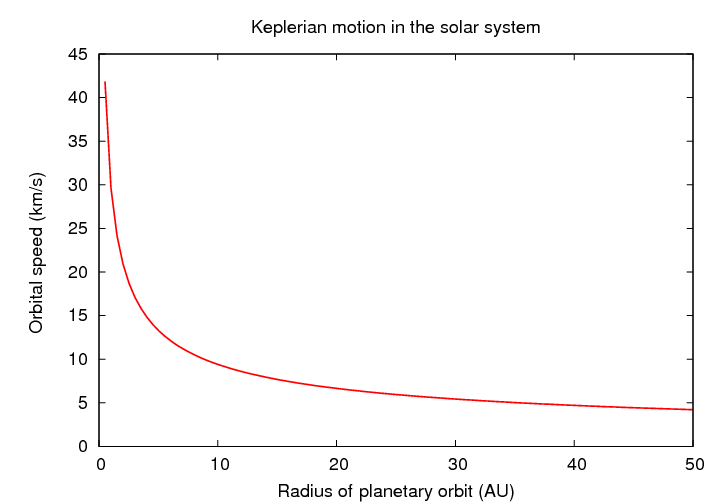
Notice how quickly the orbital speeds decrease with radius.
Right. If all, or even most, of the mass of the Milky Way Galaxy is concentrated at its center, then the rotation curve should show a sharp decrease as a function of radius.
We can be a bit more quantitative. If we know the rotational velocity at some orbital radius -- such as the Sun's radius -- then we can compute the velocity at any other radius like so:
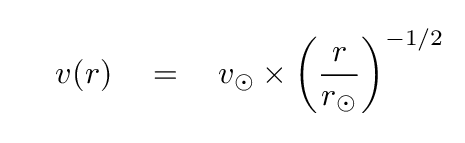
Let's use these values:
solar distance from galactic center R🞊 = 8 kpc solar orbital velocity V🞊 = 235 km/s
Assuming that our Galaxy's mass is all concentrated at the center, use the formula above to compute the orbital speed of objects at these distances.
Orbital radius r Keplerian velocity v(r)
(kpc) (km/s)
--------------------------------------------------------------
1.7
2.0
2.7
4.0
5.1
6.1
7.0
--------------------------------------------------------------
Hmmm. Does this look right?
So, let's compare this Keplerian prediction to the actual shape of the rotation curve in our Galaxy. You can look at our previous lecture to see the methods astronomers have used to measure the orbital speed of stars and gas.
The following is a summary showing a number of recent results:
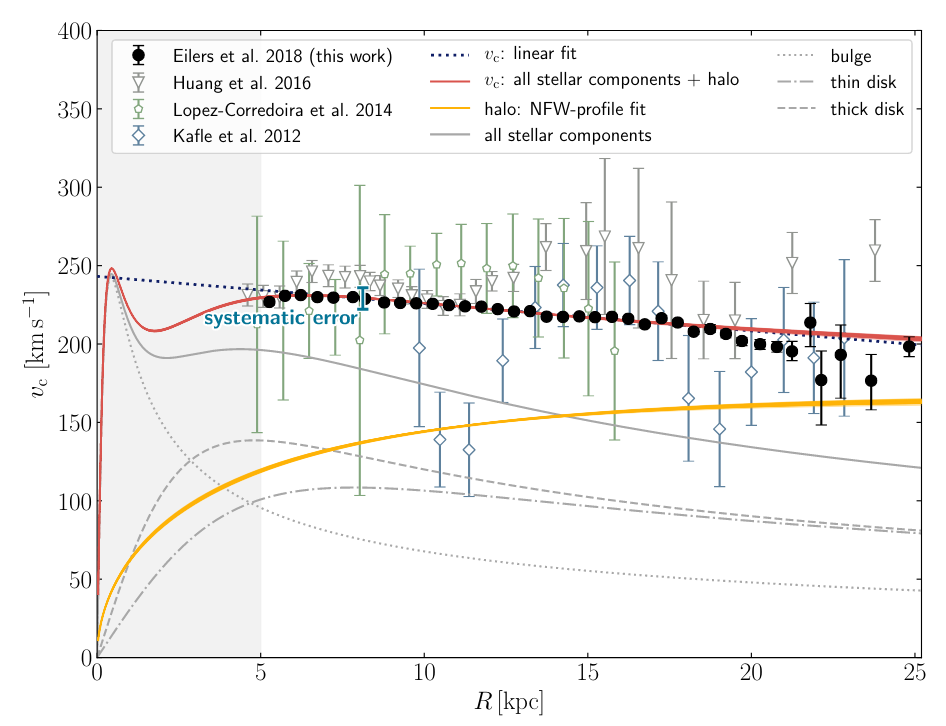
Figure 3 taken from
Eilers et al., ApJ 871, 120 (2019)
Q: Do the measurements decrease with a Keplerian pattern?
Q: If not, what does this mean about the distribution of mass
in the Milky Way
The rotation curve of the Milky Way does not decline quickly with radius, but is instead almost flat.
What does that mean? It means that the bulk of the mass CANNOT be concentrated at the center, but instead must be spread out more evenly throughout the galaxy.
Okay. We see evidence that a considerable amount of mass must be spread throughout the entire Milky Way. Can we be more specific? Is it possible to figure out how that mass is arranged?
The answer is "yes." The details are complicated, but we'll adopt a simple approximation for illustrative purposes. As Isaac Newton showed long ago,
The gravitational force at radius R due to a spherically symmetric distribution of matter is identical to that of the mass enclosed within R, all concentrated at a point at the center.
In other words, an object in a circular orbit of radius R will have a velocity given by
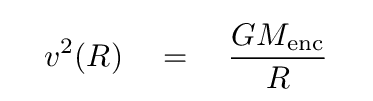
where the mass enclosed within radius R can be computed by the integral of the density over a series of spherical shells.
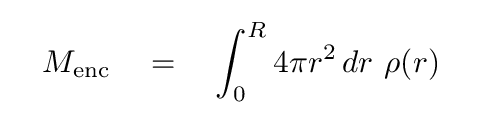
Using this approach, astronomers can estimate the mass of our Milky Way contained with a range of radii, and the derive the speed with which objects would move in circular orbits. Dealing with eccentric orbits is more complicated, so we'll leave that to the experts.
Let's practice with an example:
Q: Suppose that the density of a galaxy is constant --
the same at all radii. What sort of relationship
will we find for velocity as a function of radius?
Hmm. In that case, the circular velocity is proportional to the radius.
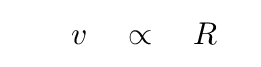
Hmmm. That doesn't sound right. That would mean that the velocity would rise and rise with greater distances from the center of the Milky Way; but that's NOT what we observe. Instead, we measure a rotation curve which rises sharply in the innermost regions, and then flattens out for a prolonged distance. One way to explain this is to imagine that the Milky Way is built from several different components:
Scientists who study galaxies sometimes combine three or four different mass components in order to create a model which reproduces the observed velocities:
Figure 3 taken from
Eilers et al., ApJ 871, 120 (2019)
Just what sort of distribution of mass WOULD give rise to a flat-ish rotation curve? Let's assume that the density can be described as a power law of the radial distance:
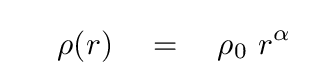
The mass enclosed within some radius R would then be
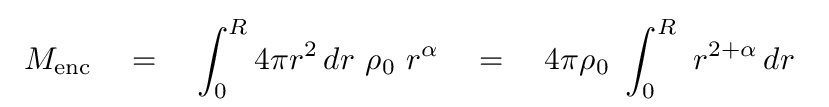
Q: How does the mass enclosed within radius R depend on R?
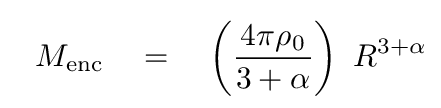
So, since this enclosed mass determines the circular velocity
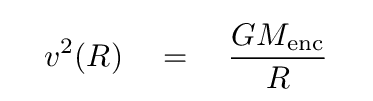
Q: What value of the density parameter α will lead
to a flat rotation curve?
Now, the rotation curve of our Milky Way is not _quite_ flat. If we want to make a more accurate estimate of the density, we can use velocities at various radii to estimate the mass enclosed at different locations. A recent review article combines results from many different studies and finds this relationship:
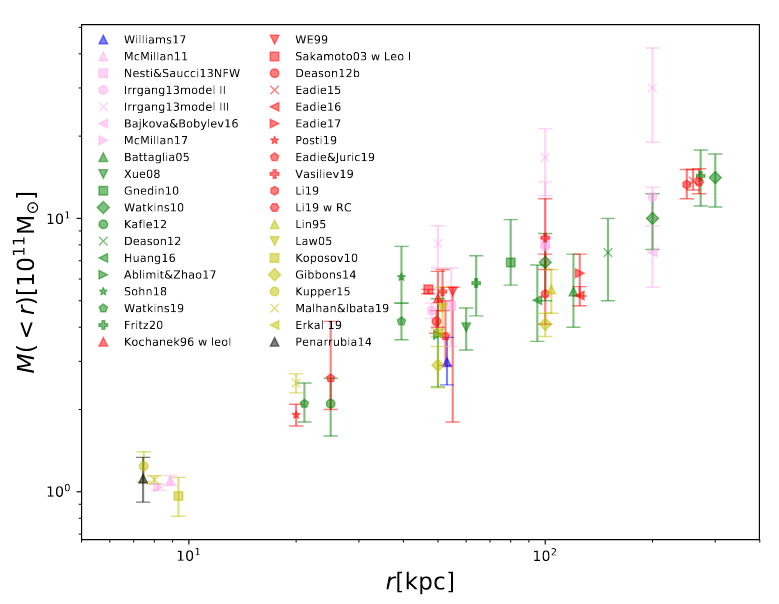
Taken from Figure 2 of
The mass of our Milky Way
by Wang et al., Science China Physics, 63, 0981 (2020)
Both axes on this graph are logarithmic. It's clear at a glance that most of the mass must be located far from the center of the Galaxy. Let's see if we can quantify that idea ...
The straight-line relationship shown in the data implies that there is a power-law relationship between the variables:
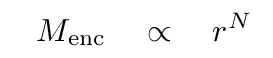
The exponent in this equation, N, should be the logarithmic slope on the graph. You can find this slope by computing the change in log(M) divided by the change in log(r).
Q: What is the logarithmic slope on this graph?
So the measurements provide one value for this exponent.
Earlier, when we calculated the mass within a sphere of variable density, we found another expression for this same exponent:
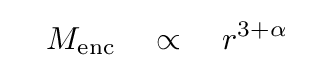
Q: Can you figure out the value of the "alpha" in this expression?
You should find approximately
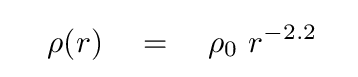
Well, good. That's not too far from the value of α = -2 which would produce a perfectly flat rotation curve.
We've been trying to figure out how MASS is distributed in our galaxy. But what about the LIGHT? Most galaxies are brighest at the center and fainter near the edges, which means the majority of the LIGHT is concentrated near the center. But, as we and other astronomers have determined, the majority of the MASS is located far from the center.
In the outer regions of our Milky Way (and other galaxies), light decreases much more rapidly than mass; the light does not trace the mass. In other words, there is a lot of mass which does not emit light.
Hmmm. I wonder what we might call this mysterious substance which produces strong gravitational forces without emitting any light ....
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.