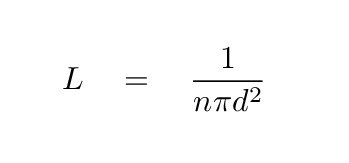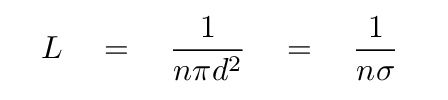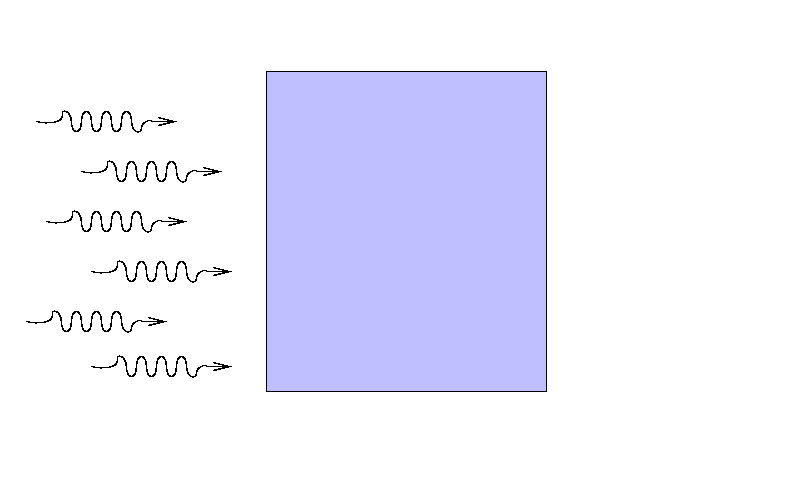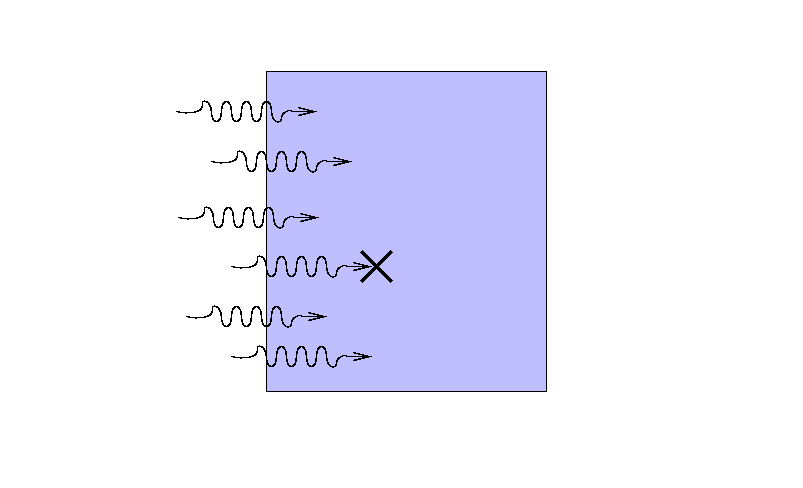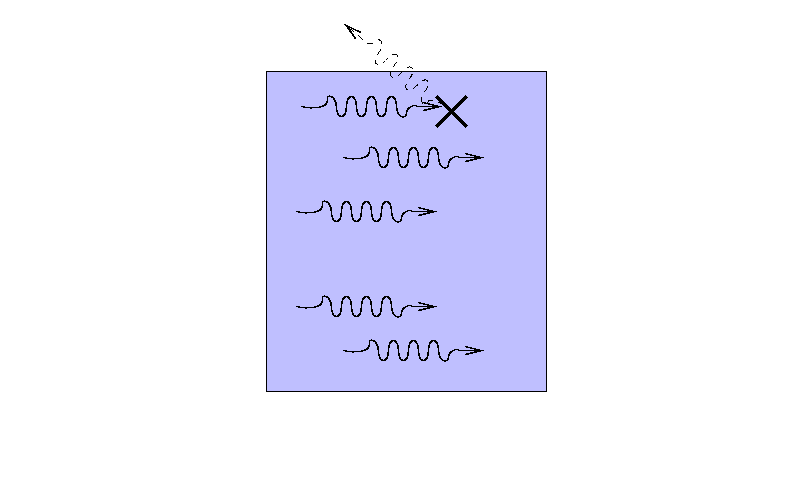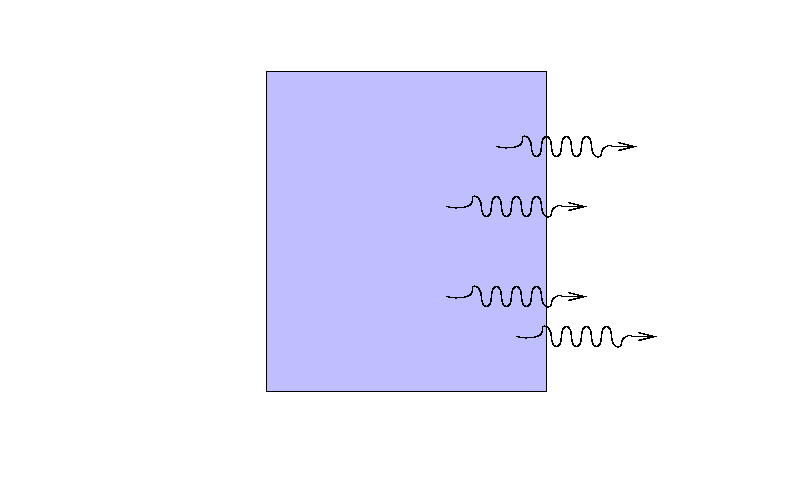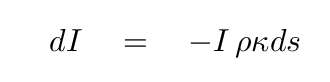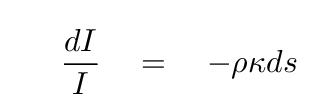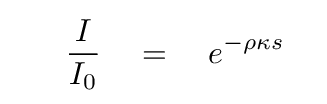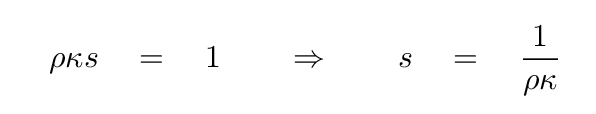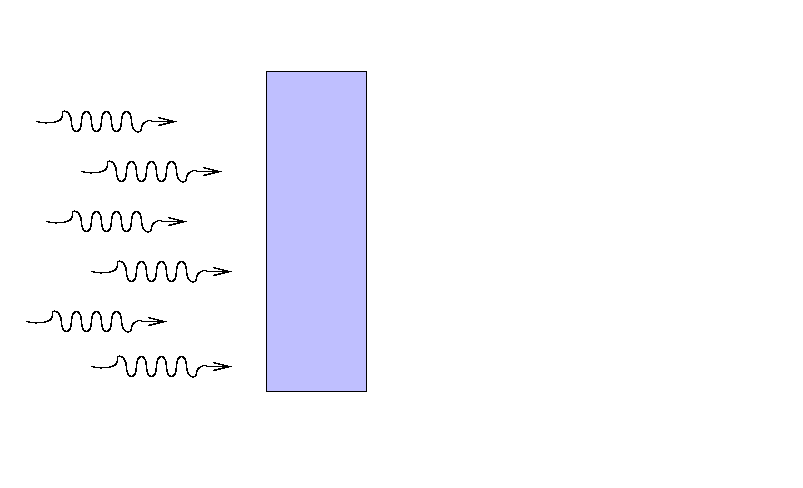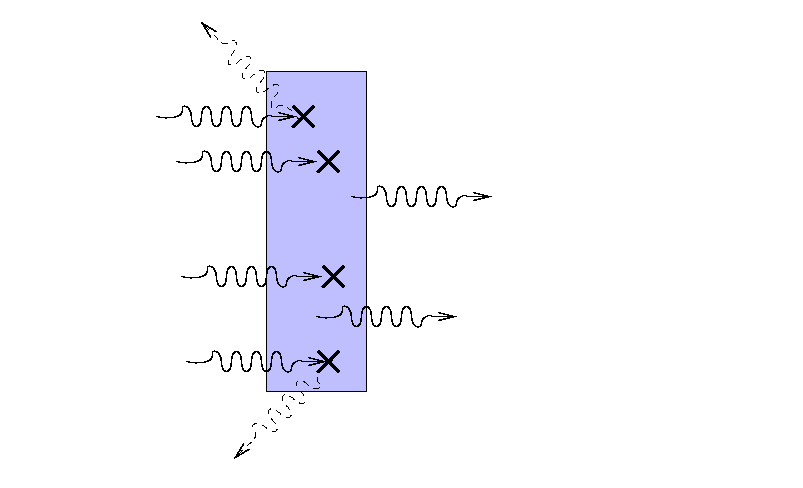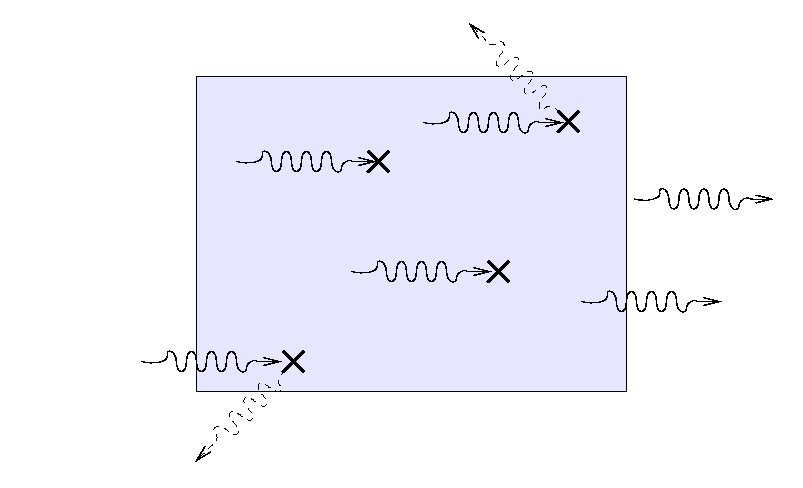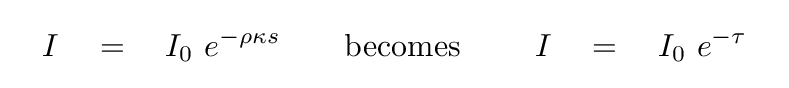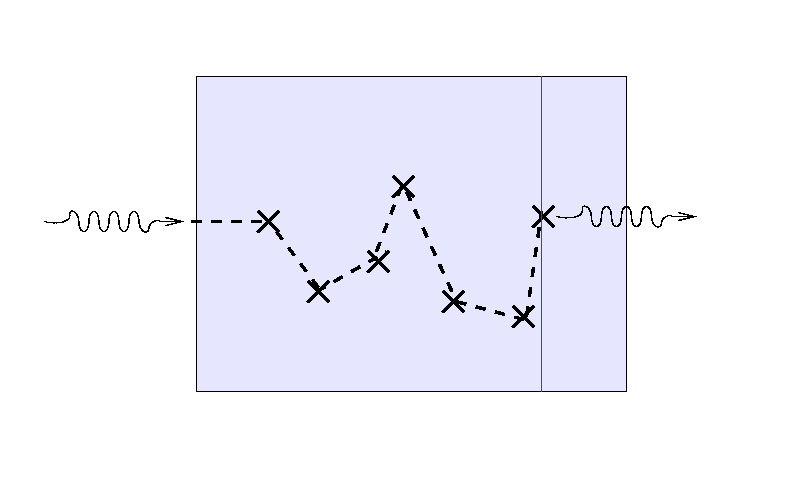Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
LTE and opacity
We are interested in the details of light's passage through
the outer layers of a star.
One of the crucial factors in this process
is the "temperature" of the gas.
But -- what exactly do we mean by "temperature"?
Is it possible to define a temperature in
these exotic regions?
It will turn out that one can define
a "temperature" in some very strict sense
only under special conditions,
called thermodynamic equilibrium,
which do not actually apply in the atmospheres
of real stars.
However, for many purposes,
one can define a sort of local thermodynamic equilibrium
which is good enough to bring theory
and observation into agreement.
Let's count the ways we could try to describe the temperature
of the photosphere of a star.
- Effective Temperature
- Measure the radius and luminosity of a star. Find the
temperature of a blackbody which would produce the
same total amount of energy:
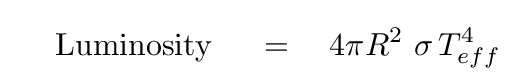
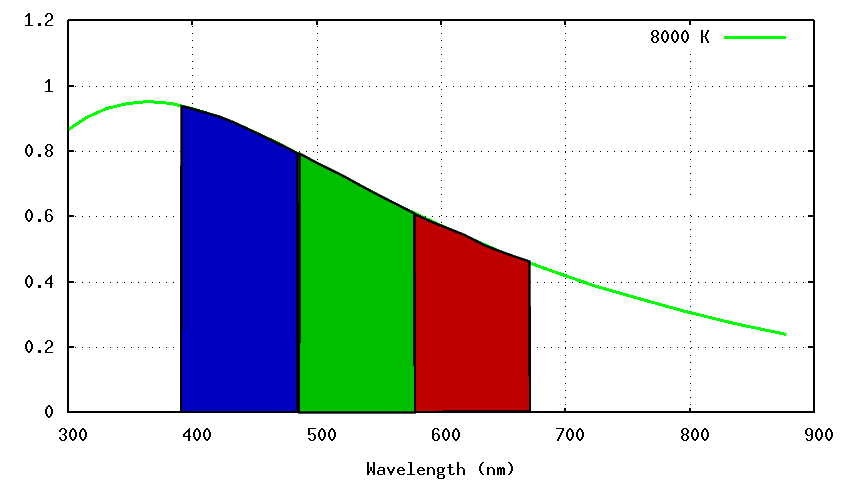
- Color Temperature
- Measure the spectrum of a star, or, more commonly,
its color via the difference of magnitudes in two filters.
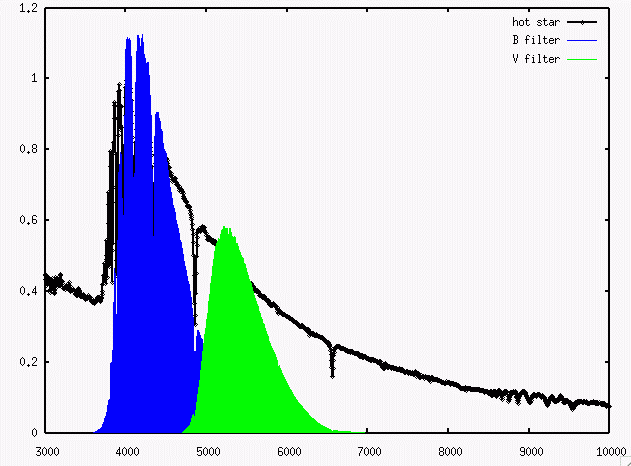
Find the
temperature of a blackbody which would produce a spectrum
yielding the same difference in magnitudes
when observed through those filters.
- Excitation temperature
- Measure the ratio of atoms in two energy levels of some
neutral atom; say, the n=2 to n=1 ratio of hydrogen.
Using the Boltzmann equation,
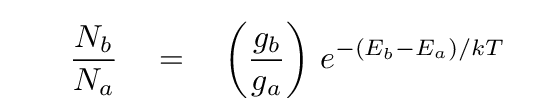
determine the temperature which would reproduce the
observed ratio.
- Ionization temperature
- Measure the ratio of atoms in two ionization stages;
say, ionized hydrogen to neutral hydrogen.
Using the Saha equation,
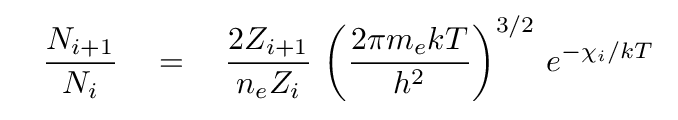
determine the temperature which would reproduce the
observed ratio.
- Kinetic temperature
- Measure the speed of particles in the gas.
If they follow a Maxwell-Boltzmann distribution,
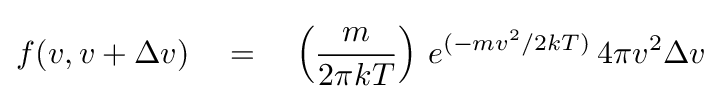
determine the temperature which would reproduce the
observed distribution.
This is often simplified to "measure some average speed
of particles, and compare to the average speed of
a Maxwell-Boltzmann distribution."
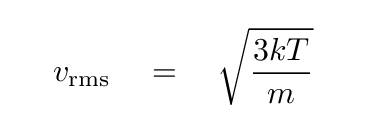
Q: Which of these is simplest to measure, in practice? What
observations would you need?
Q: Which of these is hardest to measure, in practice? What
observations would you need?
In some very simple situations,
all these temperatures might be exactly the same.
For example, if we build a box, fill it with some gas,
heat the walls of the box to a uniform and steady temperature,
and wait a bit, we will find that a single
temperature T will fit into all of these equations.
In such an ideal case, we say that the gas has achieved
thermodynamic equilibrium
(or TE for short).
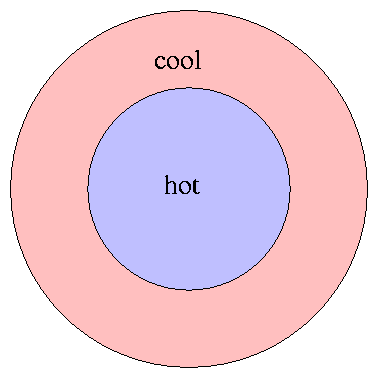
Two of the hallmarks of thermodynamic equilibrium
are isotropy -- properties are the same in all directions --
and homogeneity -- properties are the same in all places.
If we consider an entire star as a whole, neither condition
is true: the center of a star is much hotter than its outer
regions, for example.
Rats! If we are trying to understand
the detailed interaction of light and matter
inside a star, it would be very, very convenient if we could
use a single value, T, to predict the
speed of gas molecules, the excitation of atoms,
the spectrum of radiation, etc.
But it appears that real life is more complicated ....
... unless, perhaps, we can find some way
to limit ourselves to a small enough piece of the star
that matter and radiation are at least
approximately in thermodynamic equilibrium.
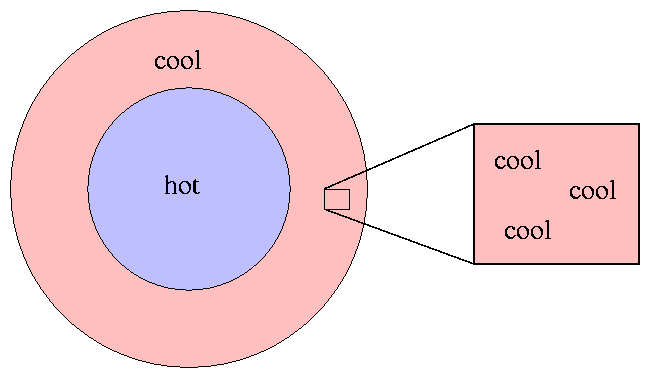
But how small does the piece have to be?
Well, one way to define such a piece
is to choose a region that
satisfies these two conditions:
- the temperature is constant over the distance that
an electron or atom moves between collisions
- the temperature is constant over the distance that
a photon moves between interactions
In colloquial terms,
we need to choose a region small enough that both
particles and photons
"see"
a constant temperature in all directions.
We can say that within this small region,
there is an equilibrium between matter and energy
which is "close enough" to thermal equilibrium.
We might say that it satisfies a
Local Thermodynamic Equilibrium,
or LTE for short.
Just how far CAN a particle travel before it probably
bumps into another particle?
Let's consider one particular
particle, moving through
a region filled with other little particles
of diameter d,
with a density of n particles per unit volume.
How far will the blue particle travel, on average, before
running into one of the other particles?
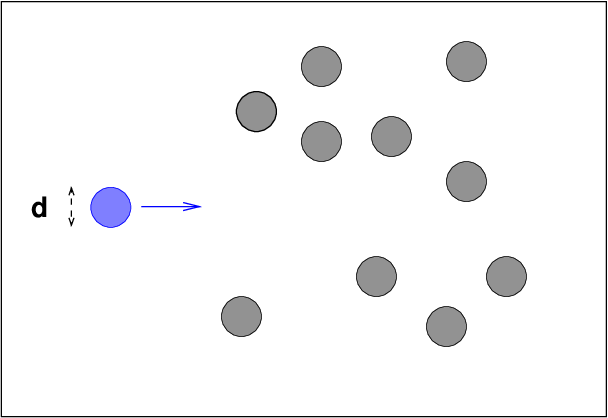
We can simplify the calculations by imagining
an equivalent situation:
- double the size of the blue particle
- shrink all the other particles down to teeny little balls of
negligible size
In this situation, collisions between the big blue particle and
the teeny balls will occur at exactly the same rate as
between the original blue particle and the other particles,
but we avoid all the tricky math to detect collisions between
spheres.
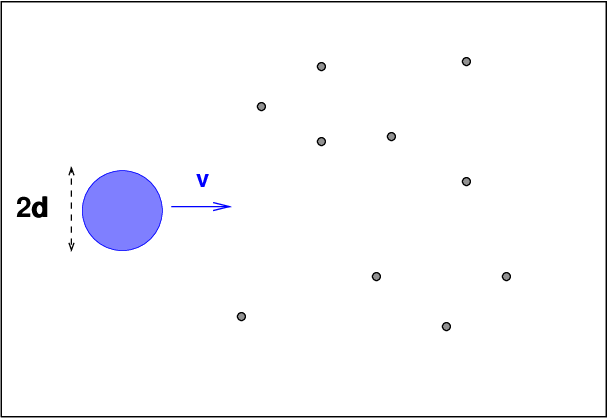
Now, as the blue particle moves through the sea
of other particles, it will sweep out a
cylindrical shape.
When the volume inside that cylinder
is equal to the typical volume occupied by a single
particle, we can expect a collision.
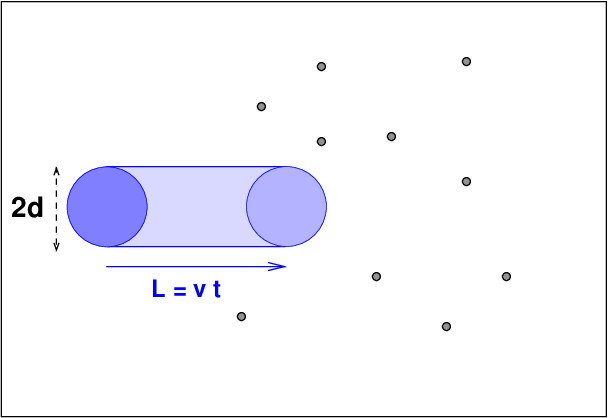
Q: What is the volume of the cylinder swept out by the blue particle?
Q: What is the typical volume occupied by a single particle?
Q: At what distance L will the two volumes be equal?
We end up with an expression for the mean free path
of a particle travelling through this region:
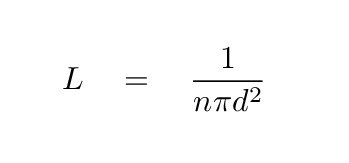
Sometimes the cross section area of the particles
(shown as πd2 in the equation above)
is denoted by the Greek letter
σ,
so that the mean free path can be written
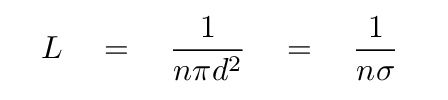
Q: Ordinary air at room temperature has a density of about 1 kg
per cubic meter. Pretend that is made entirely of oxygen
molecules, each of which has a typical size of 10-10 m.
What is the mean free path of molecules in the air?
My answer.
Let's repeat that calculation for particles in the
solar photosphere.
Q: The outer regions of the solar atmosphere -- the photosphere --
are much less dense than the air on Earth. The density
there is roughly 2.5 x 10-4 kg/m3.
Pretend that is made entirely of hydrogen atoms, each of
which has a typical size of 10-10 m.
What is the mean free path of molecules in the solar photosphere?
How does it compare to that of molecules in an ordinary room on Earth?
My answer.
We've seen how to calculate the mean free path of a particle of gas,
but what about the mean free path of a photon?
In order to do that, we need to look carefully at
the way that light dims as it travels through a cloud of material.
Suppose that a beam of light with some original
intensity I0 runs
into a slab of material.
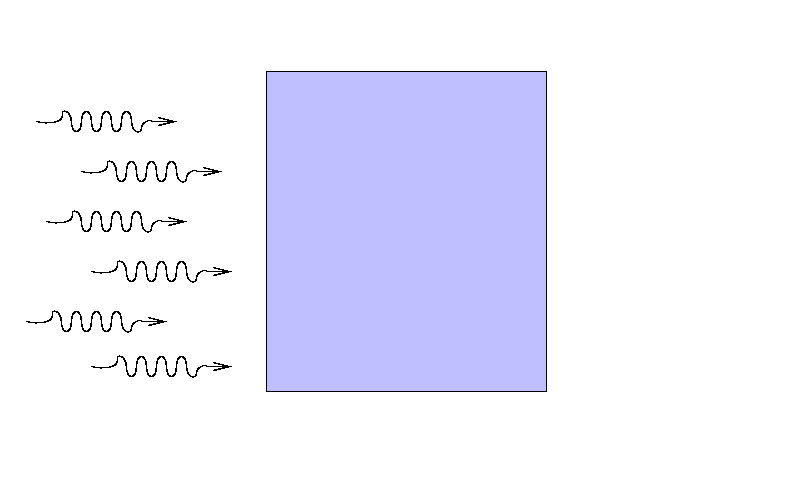
As the rays move through the material,
some may be absorbed ...
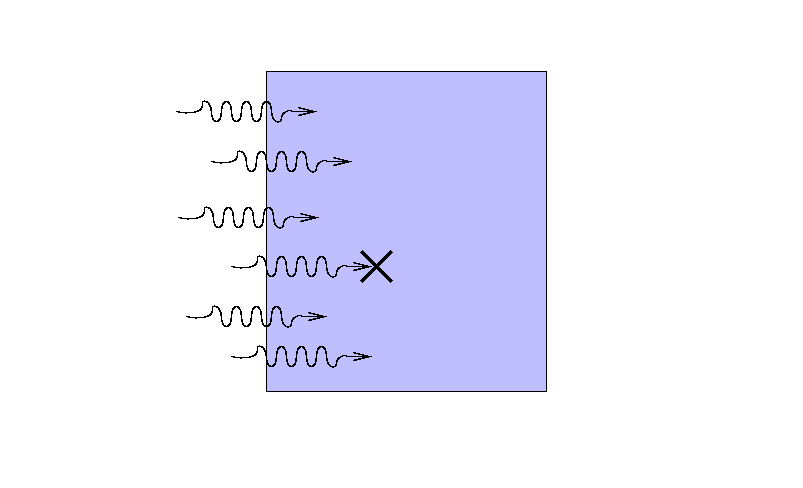
... or scattered ...
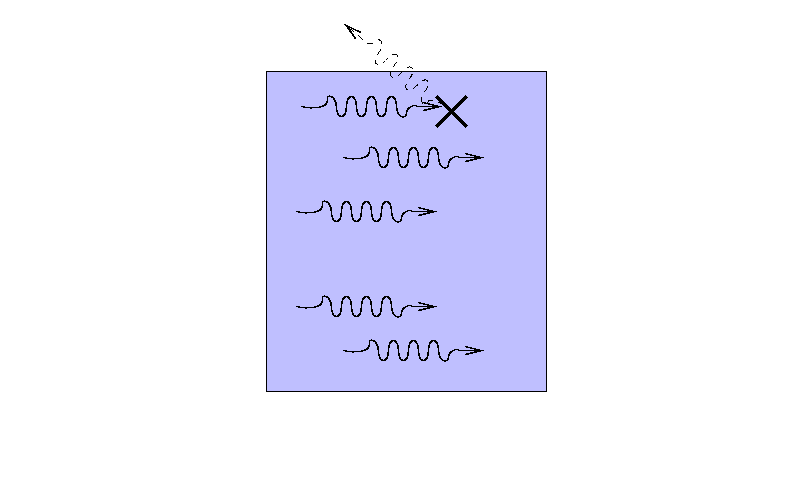
... so that only a fraction I
reaches the other side.
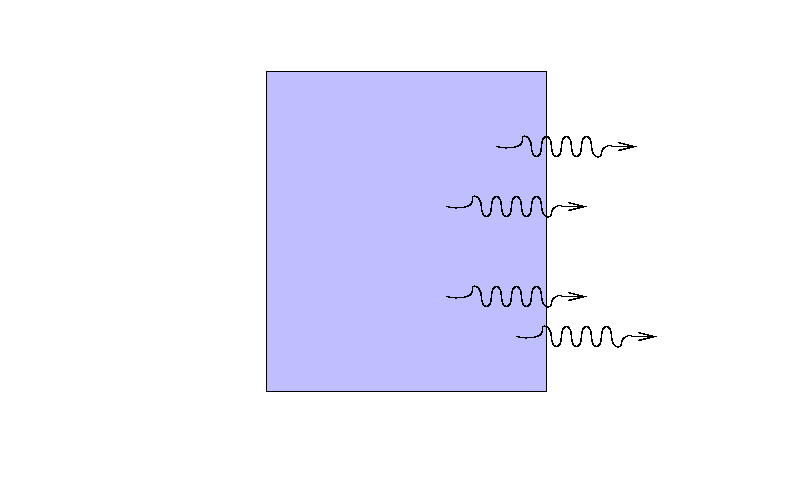
What is the ratio of the final intensity
to the original intensity?
There are several factors which must affect the intensity
in obvious ways:
- the distance s the beam travels:
the farther it goes,
the more light will be removed from it.
Units are distance (meters).
- the density of material ρ:
the larger the density,
the more light will be scattered or absorbed.
Units are mass per volume (kg per cubic meter).
- the composition of the material -- some atoms
are much more efficient at absorbing light than others.
We'll use the Greek letter κ (kappa)
to denote the opacity of the material in the slab.
Units are a bit strange: area per mass (square meters per kg)
So, if the original beam of intensity I
passes through a tiny slab of length ds,
it's reasonable to think that the
change in intensity dI
will depend linearly on these three factors:
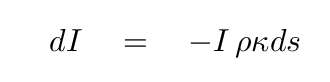
Note that the change in intensity is NEGATIVE --
after the beam of light travels through the material,
the resulting intensity must be smaller. Right?
Q: Are there any instances in which a beam of light travelling
through a slab of material can emerge with a
LARGER intensity?
My answer.
So, the relationship between the initial intensity and the
change in intensity can be written as
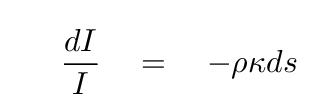
If we integrate this expression over some distance s,
we find that
the outgoing intensity I can be written in terms of the
incoming intensity I0 like so:
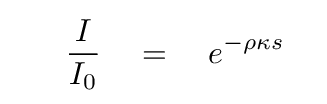
How quickly does the intensity change?
Well, the intensity will decrease to a factor of just 1/e
of its original value after a distance s such that
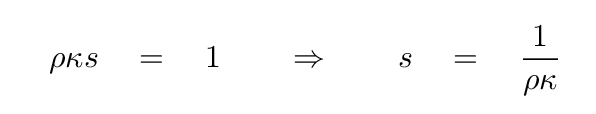
This is a useful distance to keep in mind.
We can call it the "characteristic distance"
of light travelling through the material.
We can even consider it to be the "mean free path" of a photon.
Just how big might this be in some common situations?
In the photosphere of the Sun, the opacity to optical light is
very roughly
κ = 0.0264 m2 / kg
and the density
ρ = 2.5 x 10-4 kg / m3
Q: What is the mean free path of an optical photon in the photosphere?
Q: How does that compare to the mean free path of a hydrogen atom?
My answers.
Note that we have now seen two ways to compute
the mean free path -- one more commonly used for photons,
one more commonly used for particles.

But the two expressions can be exchanged for
each other, in many cases.
If one is given the cross-section area σ
of photon-atom interactions, for example,
and the density of atoms in the cloud,
then one could compute the mean free path of a photon
through the cloud.
Consider a beam of light entering some slab of material.
The slab might be relatively narrow,
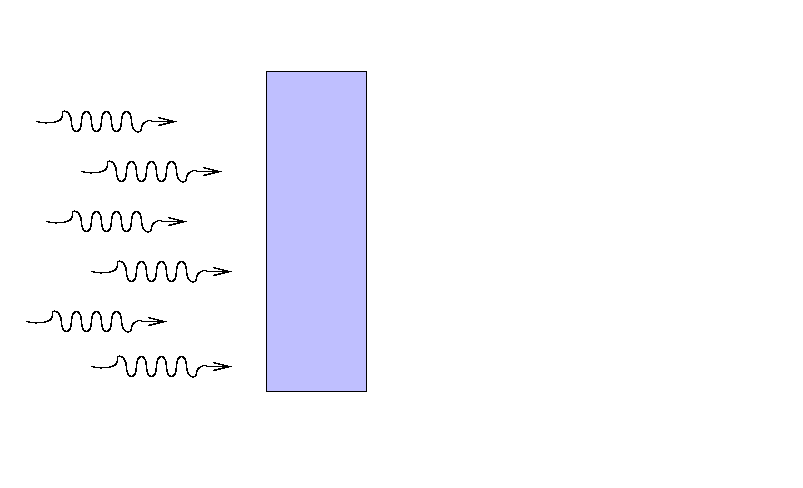
yet still block a considerable fraction of the light,
if its atoms are densely packed and efficient at interacting with light.
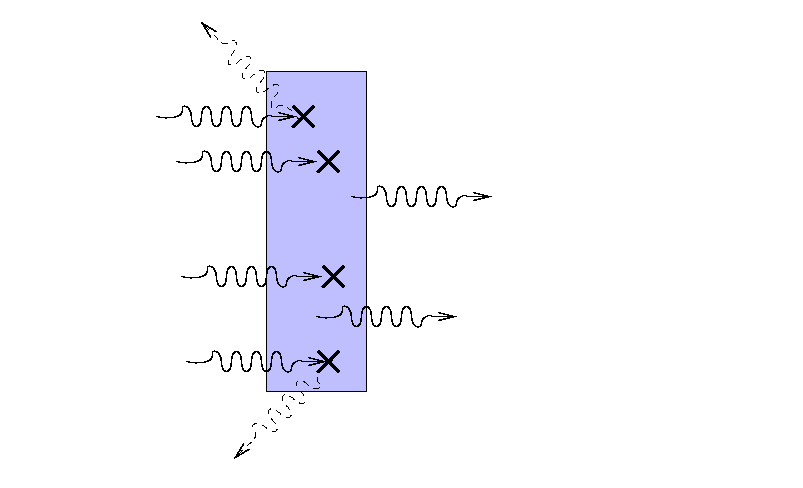
On the other hand, a much wider slab of material

with a lower opacity and/or density
might block exactly the same fraction of light,
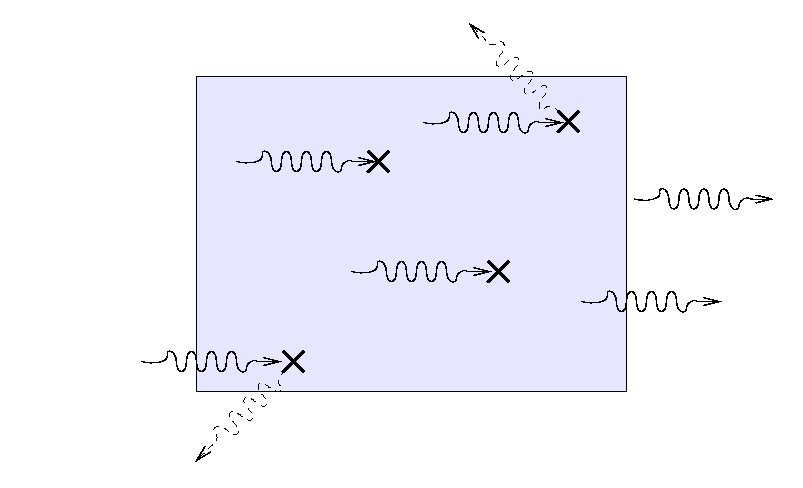
If all we care about is the fraction of light which
is blocked, or makes it through the slab,
we might combine the three factors
into a single value which expresses
"ability to block light."
Mathematically,
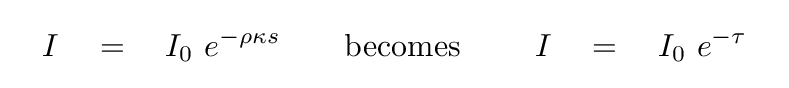
We call this variable τ the optical depth
of the slab.
Look carefully at the definition of optical depth --
it is exactly the same as "the number of mean free paths through
the slab."
The optical depth turns out have several meanings.
Consider, for example, light which must makes its way
through some scattering medium.
Suppose that the mean free path of the light is
small compared to the thickness of the material,
so that the light bounces many times before finally
escaping.
Note the location of the last bounce.
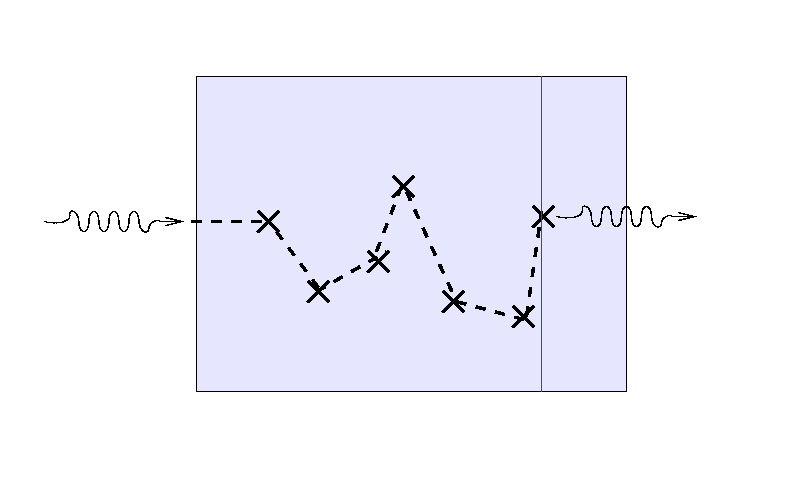
If we send a second light ray into the medium,
it will follow a different path ...
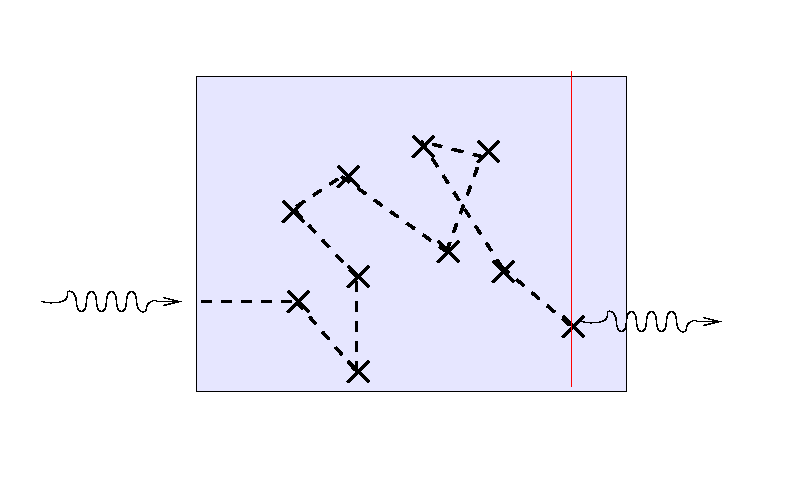
... and a third ray will again scatter randomly before
finding its way out.
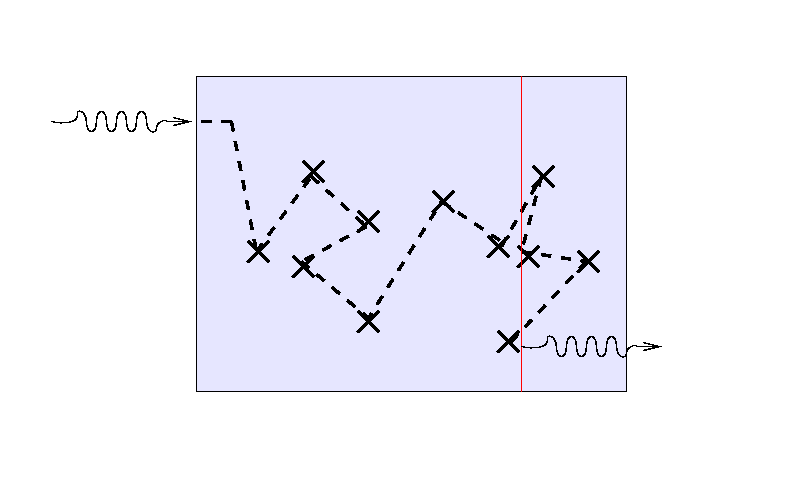
But note that the location of the final bounce tends to be
roughly one mean free path, or one optical depth,
from the outer edge
of the medium.
If we turn the situation around and ask,
"How far can we see into the slab from the outside?"
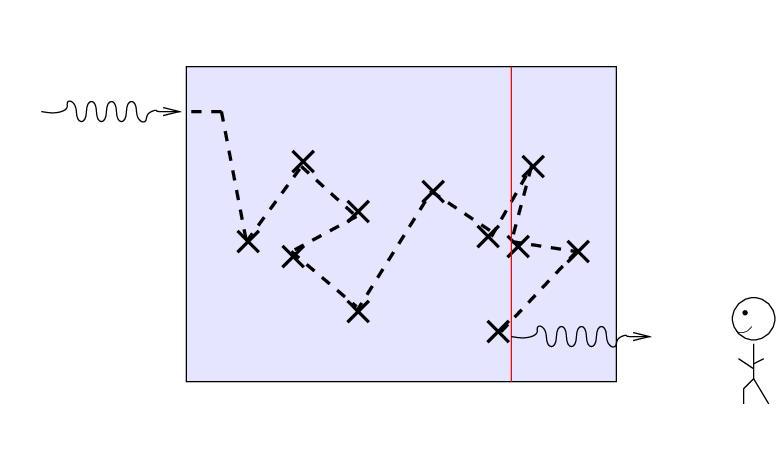
the answer turns out to be "about one mean free path",
or, equivalently, "about one optical depth."
Exercise:
- Estimate the optical depth of the Earth's atmosphere;
consider the view across a landscape from the top
of a mountain.
Perhaps these pictures will help:
- Compare the optical depth of the Earth's atmosphere to
that of the Sun's photosphere you calculated earlier.
The overall optical depth of a cloud of gas
is an important number.
It tells us right away if the cloud falls
into one of two useful regimes:
- optically thin: τ << 1
- If the gas is optically thin, then the chances are small
that a photon will interact with a single particle ...
and REALLY small that it will interact with more than one.
We can safely ignore multiple scatterings or absorptions.
In general terms, we can see right through the cloud.
Consider this example: suppose that you look at a
portion of the Earth's atmosphere on a clear, sunny day,
over a distance L = 1 km;
it has an optical depth of τ = 0.05.
Q: Send a beam of intensity I
through the gas. What fraction of
the light is blocked, and what fraction
escapes?
Q: If you double the length of the sample,
what happens to the fraction which
is blocked? What happens to the fraction
which escapes?
In the optically thin regime, the amount of extinction
(absorption plus scattering) is
simply related to the amount of material: double the
amount of stuff, double the extinction.
There is hope, then, that if we can measure the
amount of light absorbed (or emitted) by the gas,
we can calculate exactly how much gas there is.
- optically thick: τ >> 1
- If the gas is optically thick, then it is certain that
a photon will interact many, many times with particles
before it finally escapes from the cloud.
Any photon entering the cloud will have its direction
changed many times by collisions -- which means that
its "output" direction has nothing to do with its
"input" direction. In general terms, we can't see
anything at all through the cloud: it is opaque.
Consider this example: suppose that you look at a typical
portion of the atmosphere in smoggy downtown LA on a bad day.
A length of L = 1 km corresponds to an optical depth of
τ = 3.
Q: Send a beam of intensity I
through the gas. What fraction of
the light is blocked, and what fraction
escapes?
Q: If you double the length of the sample,
what happens to the fraction which
is blocked? What happens to the fraction
which escapes?
You can't see through an optically thick medium;
you can only see light emitted by the very outermost
layers. Bummer.
But there is one convenient feature of optically
thick materials: the spectrum of the light they
emit is a blackbody spectrum, or very close to it.
The opacity κ
depends on the detailed interaction of light with
the matter inside some sample of material.
It varies with a large number of factors,
such as temperature, density, chemical composition,
ionization state, and so forth.
There are many different physical mechanisms by
which matter can absorb or scatter light.
Let's try to put them into some categories.
- bound-bound κbb
-
Bound-bound interactions occur when a photon encounters
an electron which is bound to an atom, and, after the
encounter, the electron is still bound to the atom.
So, basically, either an atom absorbs the photon and jumps
up in energy,
or an excited atom drops down to a lower energy state
and emits a photon.
These interactions produce absorption and emission lines.
We
discussed line emission and absorption earlier.
In these interactions, only photons with particular energies
may participate -- all other photons will pass through
untouched. Moreover, there is no simple, general
formula describing this sort of opacity as a function
of temperature, etc.
- bound-free κbf
-
Bound-free interactions occur when a photon encounters
an electron which is bound to an atom, and,
as a result, the electron escapes the atom and flies away.
They can also occur in reverse, when a free electron
runs into an atom and is captured by it; the atom emits
a photon with the excess energy of the electron.
In these interactions, photons of any energy (above or below some
threshold) can be emitted
or absorbed; in other words, these interactions produce
a continuous spectrum.
In some cases, one can use a simple formula to describe
the bound-free opacity.
Note that in order for a photon to be absorbed in this manner
by an atom, the photon must have at least enough energy
to lift an electron from its current energy level to
n = ∞ -- that is, to ionize the atom.
Q: Consider a hydrogen atom in the n = 2 state.
How much energy must a photon have to ionize
this atom?
Q: What is the wavelength corresponding to this critical
energy?
Below is a spectrum of an A0 main sequence star.
Do you see any evidence for bound-free absorption
in this spectrum?
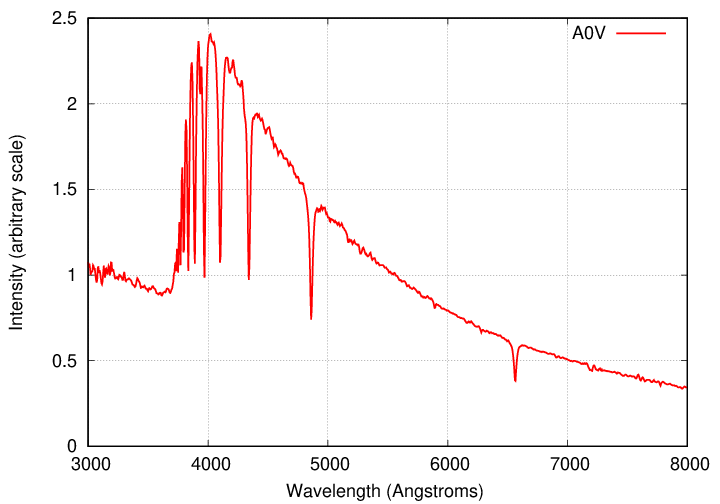
- free-free κff
-
These interactions involve a free electron flying past an
atom and either emitting a photon (and losing energy)
or absorbing a photon (and gaining energy)
as it zooms past.
Since there are no discrete energy levels involved,
photons of any energy may be involved -- this is a
continuum process.
For any particular element and ionization state,
one can find a formula providing the effective opacity;
note that it will depend on the density of electrons, too.
This process is sometimes called "brehmsstrahlung",
which is German for "braking radiation,"
because a fast electron will slow down and radiate
away its energy as it passes through some material.
- electron scattering κes
-
When a photon meets an electron in free space, away from
any atom, it may still interact with it via
"Thompson scattering" -- but this is considerably
less probable than some of the other processes.
In other words, the cross-section for electron scattering
is pretty small. This process is therefore usually
important only when no other process is likely,
because the number of free electrons is much larger than
the number of atoms/ions.
The opacity due to electron scattering can be written down
in a general formula, as the cross-section for interaction
has a constant value, independent of the photon's
energy or wavelength:
σT = 6.65 x 10-29 m2
The total opacity in some material is just the sum of all these
components.
It will, in general, depend on the wavelength of the light,
and on the properties of the material as well: density, temperature,
chemical composition, etc.
There are various formulae which can provide
some rough approximations to the opacity averaged
over all wavelengths for
a particular choice of material and temperature;
you can see two written in section 9.2 of
your textbook.
If you prefer tables with opacities for
various combinations of parameters,
one of the references in
"for more information"
provides hundreds for your perusal.
The figure below shows the overall opacity for
a solar composition
over the range of 104 to 108 Kelvin.
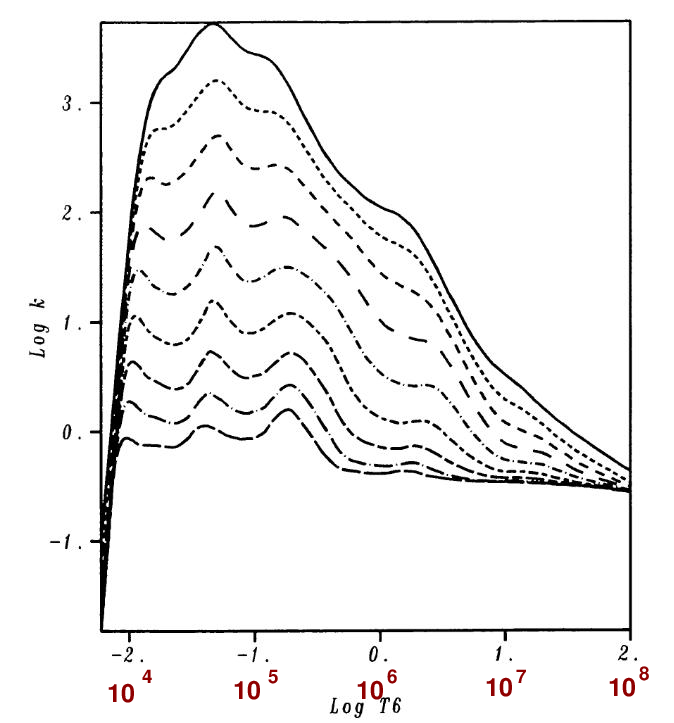
Figure 2a taken from
Rogers, F. J., and Iglesias, C. A., ApJS 79, 507 (1992)
and slightly modified
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
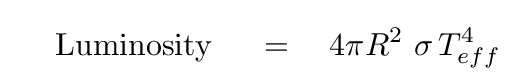


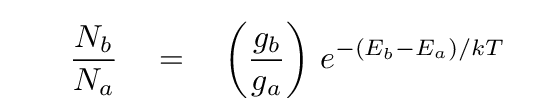
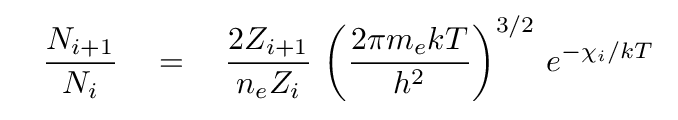
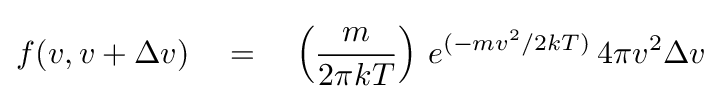
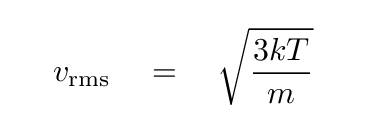
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.