 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
In this lecture, we begin our four-week-ish long study of the physics of stars. The big goal is for us to understand how stars work: how they generate energy deep in their cores via nuclear reactions, how that energy fights its way through their interiors and out towards the vaccuum of space, and how the large-scale structure of a star reflects the balance between the inward force of gravity and the outward push of other forces.
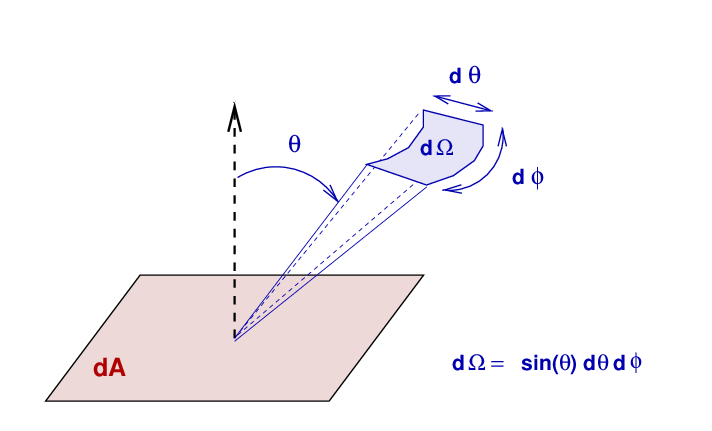
Today's topic starts with some basic physics. How can we describe the flow of energy (or photons) in terms that can be measured quantitatively? Given some particular flow of energy, how can we determine the radiation pressure associated with it?
Consider a square plate lying on the ground. It emits radiation -- perhaps because it has been heated in the Sun all day long. The question is "How much energy does it emit?"
The answer to that question depends on quite a number of factors:

Putting all these pieces together, we can express the total energy measured by our detector, Eλ dλ, in terms of a quantity called the specific intensity Iλ.

So the specific intensity is a measure of the energy carried by beams of light within a certain range of wavelengths, occupying some solid angle, at some orientation relative to its source.
Q: What are the units of specific intensity?
You may recall from our discussion of blackbody radiation that the Planck function has these same units. And, indeed, the blackbody function
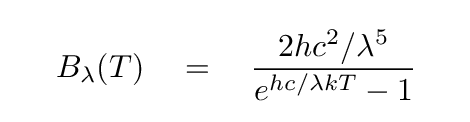
is one example of a specific intensity. It is NOT the only possible function -- there are many different physical mechanisms which create specific intensity with their own characteristics.
Our plate emits some amount of radiation in any particular direction, given by the specific intensity. If we add up all that radiation, emitted in all possible directions, and then divide by the area of all those directions, we will end up with a sort of average; this is called the mean intensity <Iλ>.
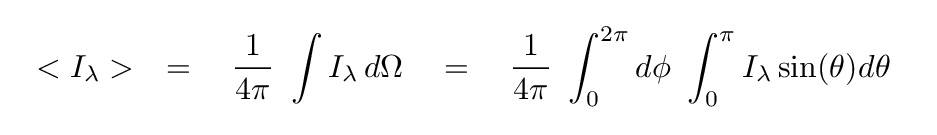
Q: What are the units of mean intensity?
In some cases, the radiation field may be the same in all directions, or "isotropic". The blackbody function is one example of such an isotropic specific intensity. In that case, we can pull the factor Iλ out of the integral, making it simpler:
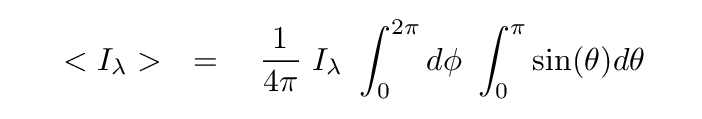
Q: What are the values of these two integrals? Q: What is the value of the entire right-hand-side?
Note that blackbody radiation IS isotropic, which means that if Iλ = Bλ, then <Iλ> = Bλ also.
Suppose that we fill a box of volume V with radiation of some specific intensity Iλ. How much energy does the radiation within the box contain?
It is possible to show (see the text) that over the range of wavelengths λ to (λ + dλ), the energy density uλ dλ has the value

Let's check the units to see if that makes sense. The mean intensity has units of (Joules) per (s * m3), so multiplying by dλ will get rid of one factor of meters in the denominator. Thus,

Does that make sense? Energy density has units of Joules per cubic meter? Yup, that sounds right. Good.
Before we continue, let's do a few rough calculations to see if we humans here on Earth ought to notice the energy of the radiation field around us. Let's consider a cube with sides of length 1 meter -- about the volume of a person sitting in a chair. How much energy does the blackbody radiation within that volume contain?
Well, a typical room has temperature T = 20 C = 293 K. Let's first compute the energy of all the blackbody photons in the optical range:
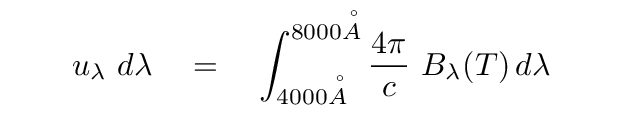
This involves a numerical integration, so I'll just tell you the answer: the energy within this cubic meter is about 3 x 10-28 Joules.
Q: Why is there so little energy in optical photons?
Yes, that's right: because the blackbody function at T = 293 K turns over and dies exponentially at wavelengths longer than the optical range. There just aren't many (or even ANY) optical photons produced by room-temperature materials.
But infrared photons -- that's a different story. Suppose we modify the limits of our integral:

Once again, I'll do the math. In this case, the energy contained in the cubic meter is about 3 x 10-7 Joules.
Aha! Now that's a LOT more energy ... about twenty orders of magnitude more energy. But does this amount of energy seem like it will have a noticeable effect on people and people-sized things?
No, probably not.
The expression for energy density can be simplified a bit in the case of a blackbody source function. As you may recall, one can integrate the Planck function over all wavelengths and end up with a reasonably compact result. In this case, the energy density of a blackbody radiation field can be derived as

Let's do an example to see if we can understand the meaning of energy density. Suppose that we sit right next to the outer atmosphere of the Sun, just inches away from gas at T = 5800 K. Surely the energy density at our location must be enormous -- right?
Q: What is the energy density of a blackbody radiation field
at T = 5800 K?
Huh. That's strange. It doesn't LOOK like a large value. After all, one Joule is a pretty small amount of energy. It takes about 4 Joules to raise the temperature of 1 gram of water by 1 degree Celcius ... so it seems as if one could sit right next to the Sun and remain cool.
But think again. Imagine a cubical glass box with sides 1 meter long, sitting next to the Sun. This value of about 0.85 Joules per cubic meter represents the energy of all the photons that are inside the box at any one moment.
The thing about photons, though, is that they don't sit still. They move fast. Really fast. The photons in the box won't remain there -- they will fly outward, away from the Sun, and off into space. New photons from the Sun will replace them inside the box, only to fly away in turn. In fact, there will be a constant FLOW of photons through the box.
Let's simplify a bit. Assume that all the energy emitted by the Sun is in the form of photons with wavelength 550 nm; that's close to the blackbody peak, so it's not a horrible assumption. The energy of one such photon is E = 3.61 x 10-19 J. Let's figure out how many of these photons must be emitted by one square meter of the Sun's photosphere in a single second.
Q: What is the total energy emitted in one second by one square meter of a
blackbody at temperature T = 5800 K?
Q: If all that energy has the form of photons with wavelength 550 nm,
each with energy 3.61 x 10^(-19) Joules, how many photons
must be emitted per second?
So, this little patch of the Sun emits a LOT of photons over the course of one second. What do those photons do? They fly away from the surface at c = 3 x 108 m/s, of course. If we imagine that they all fly straight away from the Sun, normal to the surface, then they will fill a very long, thin, rectangular box after one second has passed.
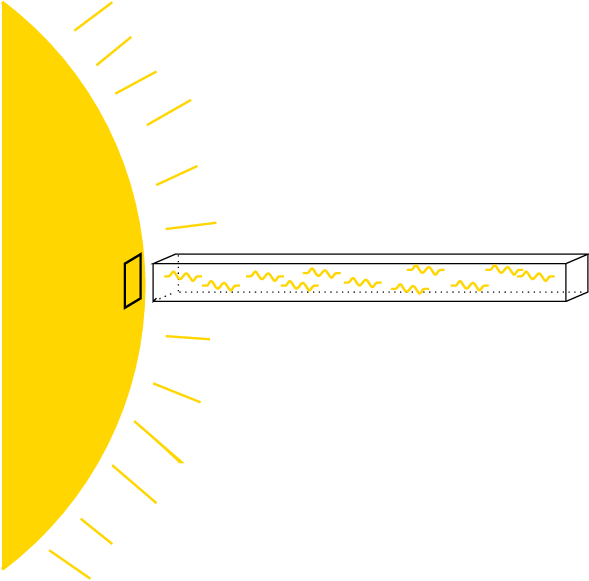
The box will have a width of 1 m, height of 1 m, and a length of 3 x 108 m. Clearly, the box has a volume of V = 3 x 108 cubic meters.
Q: What is the number density of photons per cubic meter
inside the box?
Q: What is the energy density of the photons inside the box?
So the energy inside the little box next to the Sun AT ANY ONE INSTANT FROZEN IN TIME is tiny ... but the flow of energy through the box is very rapid; the photons travel fast. If you were to sit inside the box for one entire second, a total of over 60 million Joules of energy would impinge upon you.
The heat capacity of human flesh is roughly the same as water,
about 4186 Joules per kg per degree Celsius.
Q: If a person with mass m = 50 kg absorbs 60 million Joules
of energy, how many degrees Celsius will the person's
body temperature rise?
Yet another quantity which will be useful in some situations is a measure of the NET energy within some range of wavelengths, passing through some given area per second, in some particular direction. We call this radiative flux. In order to compute this quantity, we integrate the specific intensity Iλ over all solid angles.

What are the units of radiative flux? Well, specific intensity has units of Joules per second sq. meter per meter per steradian. Here, we have just integrated over solid angle, so that would leave Joules per second per square meter per meter, or Joules per second per meter3.
However, it is often the custom to write the combination of radiative flux over some interval of wavelengths, as I've done above: Fλ dλ. That removes one factor of "per meter" from the expression, so that this combination has the actually-measurable units of Joules per second per square meter, or Joules per second per meter2. That combination of "energy per second per square area" is what we usually refer to as a "flux."
This is an important quantity, because it is one that many of our instruments actually measure. We point a telescope of some known collecting area A at the sky, expose for some period of time t, and measure some quantity of energy entering our detector over a passband Δλ.

There is a small detail connected to radiative flux and specific intensity which is particular relevant to astronomers who study young galaxies at high redshifts. Under ordinary circumstances, as when we study, say, stars in our own Milky Way, our targets are unresolved. In other words, they appear as tiny points of light, all the light concentrated within a single point-spread-function (PSF). The flux we measure depends on the luminosity of the source and its distance from the Earth.

Q: What would happen to the flux of a point source
if we moved the target twice as far from the Earth?
Right. The flux would decrease to 2-2 = 1/4 of its original value. It's the inverse square law, plain and simple.
Under these circumstances, when we observe an unresolved source, we are seeing all the light from the source emitted from its entire surface visible from our location. Strictly speaking, this corresponds to the radiative flux; it integrates over the entire solid angle of the target.
unresolved source ---> radiative flux
But suppose that our target was an EXTENDED source, much larger than the aperture we were using to extract light in our images; moreover, suppose further that the surface brightness of the source is uniform (in other words, the source is equally bright near its center and around its edges). In that case, if we were to move the target to a new distance, twice as far from the Earth,

The key point here is that moving the source farther away allows light from its outer regions -- which were outside our measurement aperture originally -- to fall into the aperture. In this only slightly contrived and simplified case, the flux we measure from the object would REMAIN CONSTANT as we moved the object farther away from the Earth!
In this case, we aren't observing light from all regions of the object; instead, we're only measuring light which is emitted from some small solid angle, equal to the solid angle of our measurement aperture. So the quantity corresponding to the measurement in this case is specific intensity.
resolved source, measured through aperture smaller than the source
----> specific intensity
You may recall from basic phyics that pressure is defined as the force exerted over some area. But note that the units of pressure can also be expressed in terms of energy.
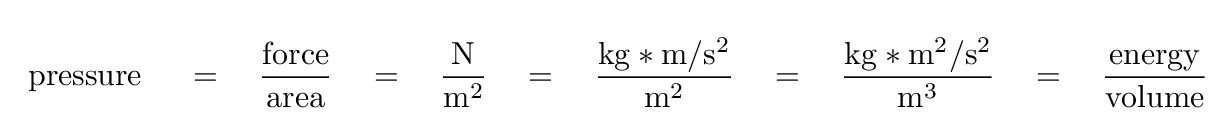
Earlier, we found several ways to compute the energy density of a radiation field, such as

and

Note that these expressions have exactly the same units. It appears that there may be some connection between the energy density of a radiation field and the pressure it exerts.
As one can see by reading section 9.1 of the text, one can figure out how the momentum transferred by photons corresponds to a pressure. One starts with the simple reflection of a single photon
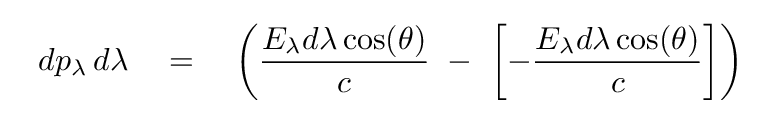
and integrates over all solid angles from which photons can arrive, yielding a rather complex expression

Fortunately, if the specific intensity Iλ is isotropic -- as is true for blackbody radiation -- then we can pull it out of the integrals over angles. Those integrals yield (2 π) and (2/3), respectively, so that in this simple case, the pressure of radiation is just

But wait --- it simplifies even further! For the special case of blackbody radiation, we can integrate over all wavelengths and end up with a simple result.

That final expression ought to look familiar. Go back to our derivation of the energy density u of blackbody radation, and you'll see that it is ALMOST the same. The only difference is a factor of 1/3.
The bottom line is that we now have a relatively quick way to determine the pressure exerted by radiation under the common situation that the light is produced by a blackbody. What good is that? Well, among other things, it might help us to design a spaceship!

Image courtesy of
The Planetary Society
In theory, if one places a very lightweight and reflective object into space, then the radiation pressure of sunlight might push it hard enough to alter its trajectory. We call such devices "solar sails". For decades, they were found only in science fiction, but in the past 20 years, several actual sails have been tested in space.
Let's see how they might work. Imagine a simple 1-meter-by-1-meter square of aluminum foil placed next to the Sun, just a few meters from the photosphere. Pretend that the foil is perfectly reflective.
The thickness of foil is 16 micrometers, and the density of aluminum
is 2700 kg / cubic meter.
Q: What is the mass of this sail?
Q: If the Sun emits as a blackbody at T = 5800 K, what is the
what is the radiation pressure on the sail?
This is equivalent to the force on the sail, pushing
away from the Sun.
On the other hand, gravity pulls the sail back toward the Sun.
Using the values
G = 6.67 x 10^(-11) N*kg^2/m^2
M = 2 x 10^(30) kg solar mass
R = 6.95 x 10^(8) m solar radius
Q: What is the force of gravity on the sail?
Q: If we place the sail next to the Sun, and release it
from rest ... what happens?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.