
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Today, we look at the portion of a star's life which corresponds to "childhood" -- the time between the initial collapse of a large cloud of gas, and the point at which the star reaches a stable and long-lived equilibrium on the main sequence.
The first stage of a cloud's collapse is called the "freefall stage", because each chunk of gas falls inward, toward the center of the cloud, without interacting very strongly with other chunks. In real life, the cloud soon forms regions of different density (higher in the inner regions, lower in the outer regions), but we if we pretend that the density remains uniform as it shrinks, we can use some basic physics to determine the timescale. You can find the details shown in your textbook, but the bottom line is that a large spherical cloud of initial density ρ0 will shrink down to size zero (or, at least, "very much smaller") in the "freefall timescale"

Q: Why doesn't the initial size of the cloud appear in this equation?
Q: Suppose that a cloud of 1 solar mass, M = 1.99 x 1030 kg,
has an initial radius of 0.1 pc, R = 3 x 1015 m.
Roughly how long will it take this cloud to collapse?
During this collapse, the cloud loses a large amount of gravitational potential energy (GPE). If we compute the GPE of the cloud in its initial, large, size, and then the GPE after it has shrunk down to its final size, we can calculate the amount of GPE which is liberated in the collapse. Most of this energy heats up the gas and causes it to radiate the energy away as light in the infrared region.
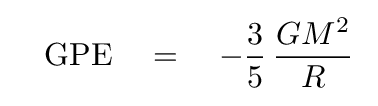
For example, consider a cloud which will eventually turn into a Sun-like star.
Q: What is the change in GPE during this collapse?
Q: Divide the released GPE by the freefall timescale to estimate
a very rough "freefall luminosity".
As you can see, the power radiated by the collapsing cloud is larger than that of our current main-sequence Sun. Young stars can be very luminous; and, as we will see shortly, as stars like the Sun form, they gradually DECREASE in luminosity as the release of gravitational energy is replaced by energy generated by nuclear reactions.
We'll return to this issue in a moment, but first, let's address one important issue: fragmentation.
The clouds of gas and dust we see in star-forming regions are large -- VERY large. Many of them contains thousands or even millions of solar masses of material, and stretch across regions of space many parsecs in size.

Image courtesy of
NASA, ESA and the Hubble Heritage (STScI/AURA)-ESA/Hubble Collaboration
Will a single giant molecular clouds turn into a single giant star, thousands of times more massive than our Sun?
NO!
Why not? Because as the cloud collapses, some regions tend to become more dense than the rest. And if one region has a higher density, it will have a smaller free-fall time -- which means it will collapse faster, achieving a still high density, which makes it collapse faster ... and so on. The inner regions of a big cloud will soon detach themselves kinematically from the outer regions.
In addition, giant clouds are not static: they contain swirling eddies which pull the gas this way and that, and they suffer gravitational perturbations from passing stars and other molecular clouds. The resulting internal motions break up the cloud into semi-isolated sectors, which start to collapse independently of others. Once a sector begins to shrink, it becomes even more isolated.
The net result is that a single giant molecular cloud breaks up into hundreds or thousands of smaller clumps or cores or globules, each of which may collapse into a star or multiple-star system. You can see some of these globules in a close-up view of the Eagle Nebula.

Image courtesy of
NASA, ESA and the Hubble Heritage (STScI/AURA)-ESA/Hubble Collaboration
Fragmentation is a complex phenomenon which we don't understand very well. For one thing, not all the fragments are the same size and mass. It turns out that low-mass clumps form much more readily than high-mass clumps. The relative number of stars of different masses which are created by a single cloud is known as the initial mass function (IMF). Astronomers have tried to measure the IMF in different star-forming regions in the Milky Way, and in other galaxies as well. Although the general form of the IMF seems similar in many places, the exact parameters -- the slopes of these lines, and the mass at which the function peaks -- vary quite a bit.
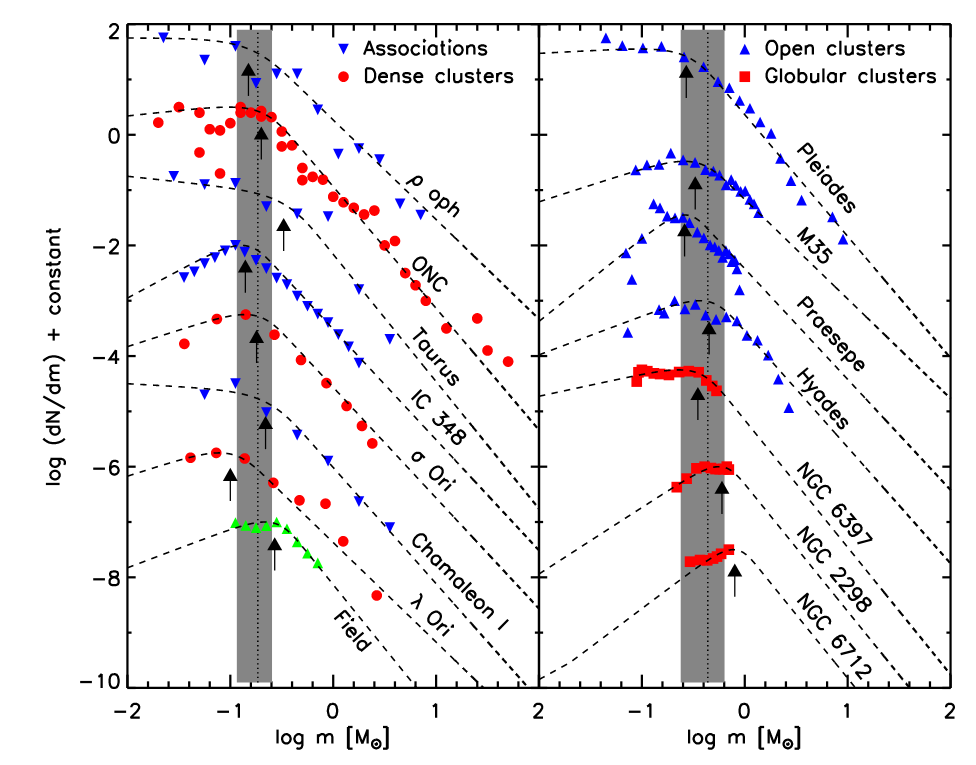
Image taken from Figure 3 of
Bastian, Covey and Meyer, ARA&A, 48, 339 (2010)
Okay, let's go back to the evolution of a cloud of gas as it turns into a star. Our calculations of the "free-fall" luminosity for a 1-solar-mass cloud suggest that during the brief free-fall phase, the cloud may emit much more power than the final main-sequence star. What would happen if we tried to place that collapsing cloud on the HR diagram?
Well, we know that it should appear ABOVE the sun's location on the main sequence, since it is more luminous. But what about the horizontal location of this proto-star?
Q: How does the temperature of the exterior of this collapsing cloud
compare to the current photospheric temperature of the Sun?
Yes, that's right: the cloud may be radiating a very large luminosity, but it does so over an even more larger area; after all, the cloud's radius is orders of magnitude larger than the Sun's. The result is a lower temperature.
The details, of course, are much more complicated. The first person to work them out systematically, and predict the path of a collapsing star on the HR diagram, was Chushiro Hayashi. The diagram below is taken from a paper he published in 1965.
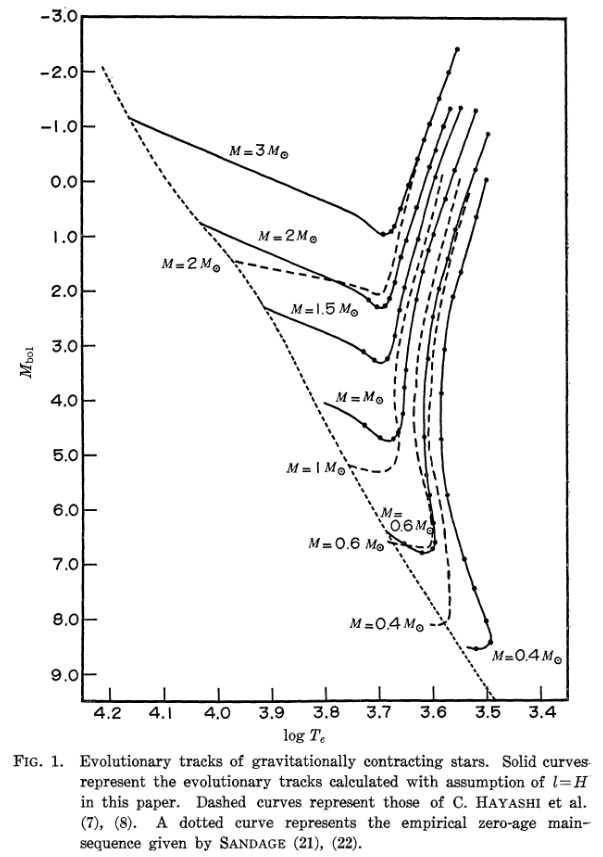
Figure 1 of
Hayashi, PASJ 17, 177 (1965)
Note how the shape of the Hayashi tracks changes with mass: low-mass tracks are nearly vertical, while those of higher-mass stars veer to the left in the later stages.
Do real stars follow these theoretical tracks? It's a bit hard to confirm, since even the "short" timescale of a few hundred thousand years is considerably longer than the lifetime of a single astronomer (or human civilization, for that matter). However, there certainly are many, many objects observed in star-forming regions which lie in the area above the main sequence.
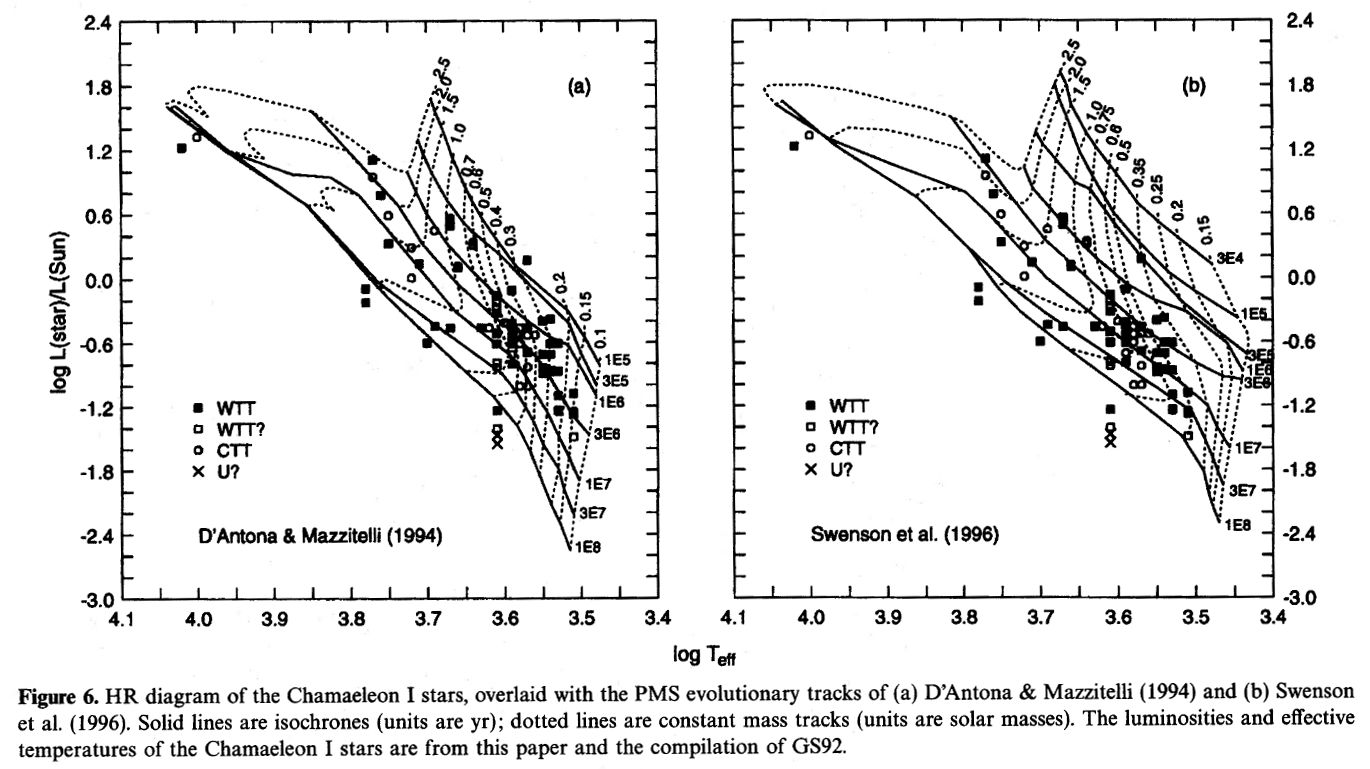
Image taken from Figure 6 of
Lawson, Feigelson & Huenemoerder, MNRAS 280, 1071 (1996)
Bastian, Covey and Meyer, ARA&A, 48, 339 (2010)
Eventually, the free-fall phase comes to an end when the density of the proto-star grows so high that radiation can no longer easily escape from the interior; in other words, when the density -- and thus opacity -- increases to the point that the cloud becomes optically thick to infrared radiation.
If the energy released by gravitational collapse can't be radiated away into space immediately, it heats up the gas in the innermost regions. The thermal motions of the hot gas resist the pull of gravity, and the free-fall collapse turns into a gradual shrinking. The core region continues to increase in density and temperature, until at last nuclear reactions begin. The object reaches the main sequence, and life as ordinary star begins.
Actually, there's one minor point in this last step that I find interesting. As the temperature of the core gradually rises, certain nuclear reactions with a lower temperature threshold will take place before the regular proton-proton or CNO chains. One of these low-temperature reactions is the fusion of deuterium into helium.
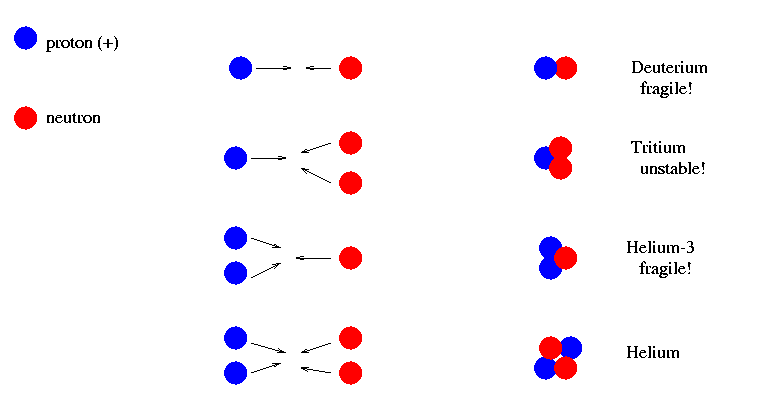
The facts that
means not only that deuterium will be consumed by fusion in the core of a young star, but that deuterium-containing material from the middle and surface layers will be mixed into the core as well. The result is that young stars are basically deuterium-destroying factories. Almost all the deuterium present in the original cloud of gas will be converted into helium and other products by the time the star reaches the main sequence.
"So what?" you might ask. "Who cares about deuterium?"
Cosmologists, that's who. It turns out that the abundance of deuterium in the universe is a giant clue to the nature of the universe. The fate of the universe -- will it expand forever, or slow down and stop? -- depends in large part on the average density of the universe in the first few minutes after the Big Bang. Look at the chart below.

Image courtesy of
NASA/WMAP Science Team
Notice how sensitive the deuterium abundance is on the average density of the universe. If we could measure the primordial deuterium abundance accurately, we could pin down large-scale properties of our universe!
But those stupid young stars have destroyed much of it. Aarrrggghhhhh.
When we look at individual clumps of gas which have recently collapsed to form very young stellar objects, we see that many of them look a bit ... strange. Instead of being spherical, many show flattened shapes; disks, in other words.
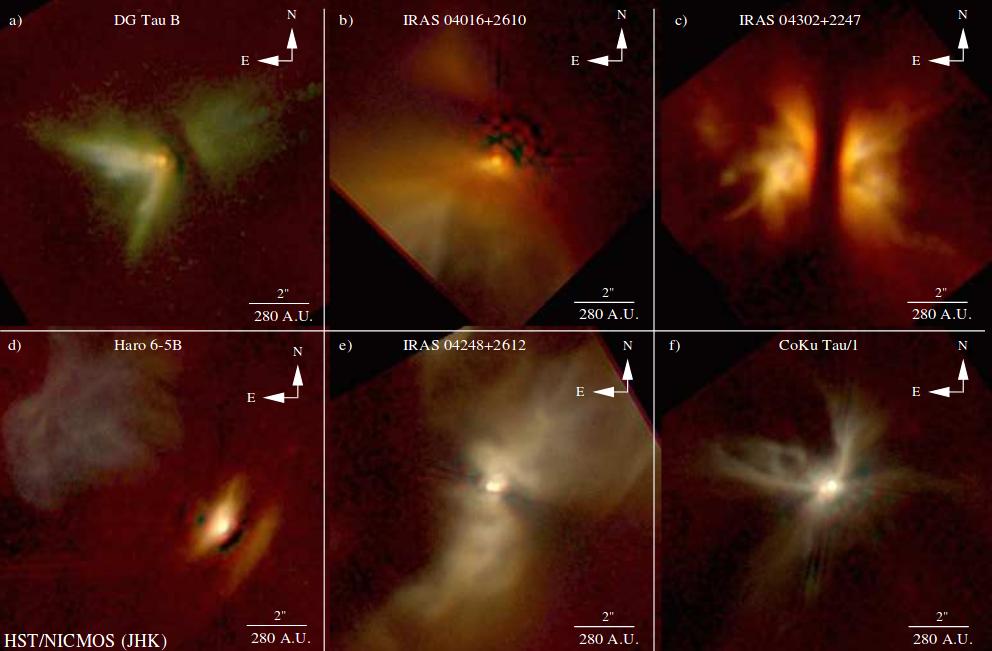
Figure 1 taken from
Padgett et al., AJ 117, 1490 (1999)
The reason that a collapsing cloud of gas is likely to turn into a flattened disk is a bit complicated, and involves both collisions and the importance of angular momentum. You can read a basic explanation if you wish. But the result is clear: many young stars are surrounded by circular disks, and some even show jets.

Images courtesy of
ESO/H. Avenhaus et al./E. Sissa et al./DARTT-S and SHINE collaborations
The material orbiting in a circumstellar disk around a young stellar object will absorb energy from the star; material close to the star grow hot, while gas and dust far from the star will be cool. That much is obvious. But can we determine QUANTITATIVELY the temperature of material at some particular distance from the star? In real life, there are many complications, but we can make a very simple model that turns out to yield decent results.
Consider a spherical object of radius R which is circles the star at some orbital radius a. For convenience, I'll call the object a "planet," but it doesn't have to be big -- exactly the same equations apply to a sphere the size of a mountain, or a baseball, or even a grain of sand. We'll ignore complications such as the albedo of the object in this derivation.
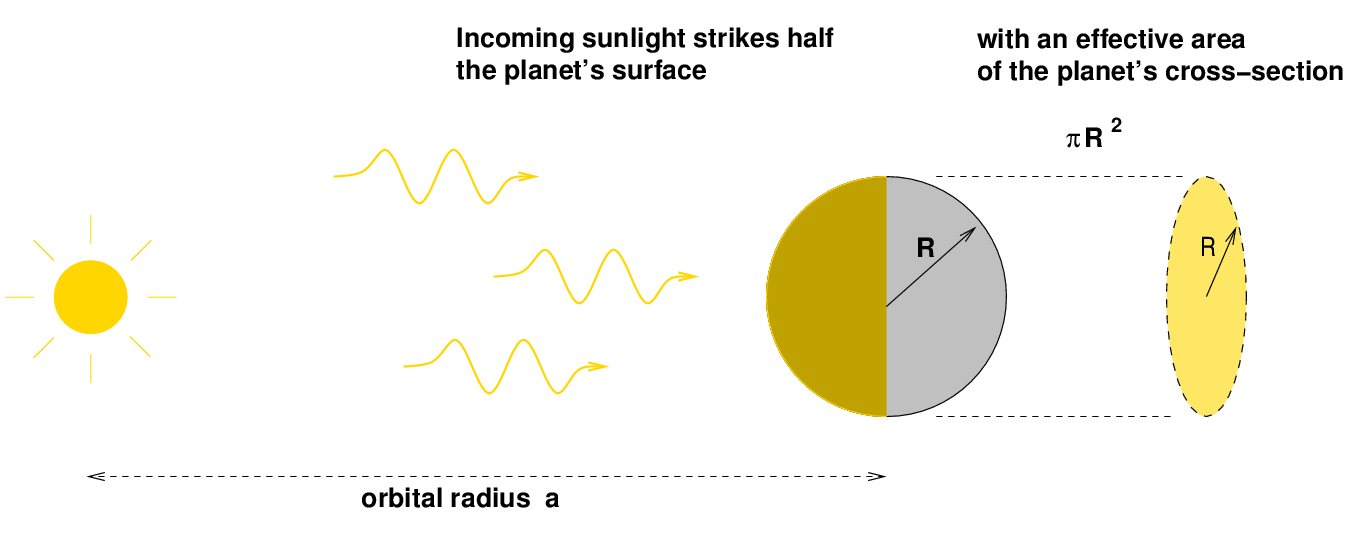
We can derive the amount of incoming energy striking the planet each second:
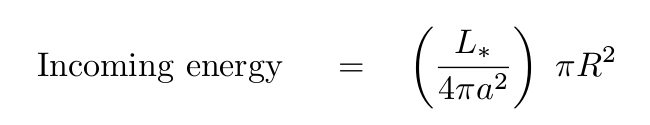
Now, if we simplify a LOT and assume that the entire planet has exactly the same temperature, and ignore the emissivity of its surface, we can figure out the amount of energy that it radiates away into space each second due to thermal radiation:
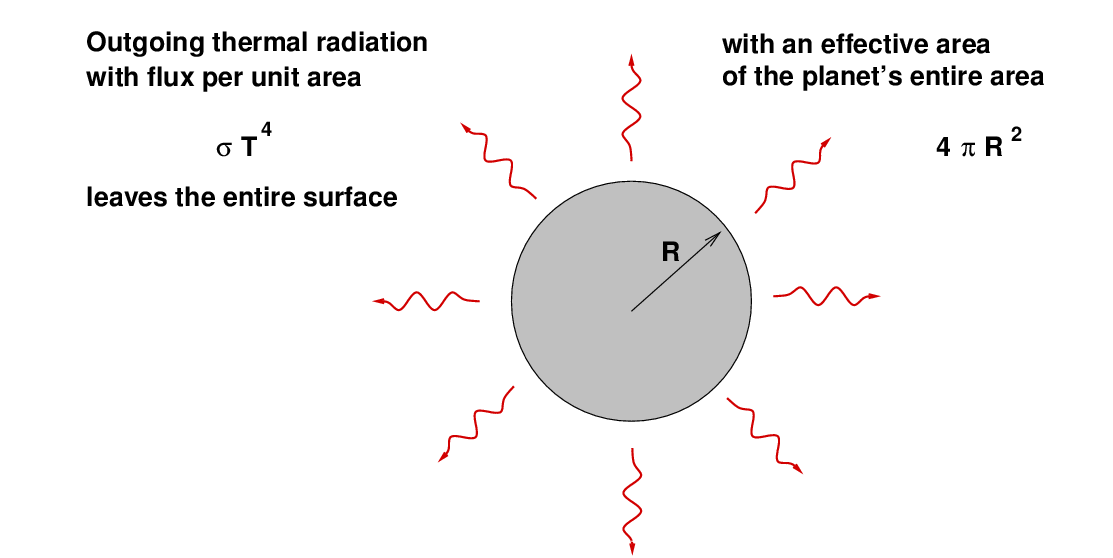
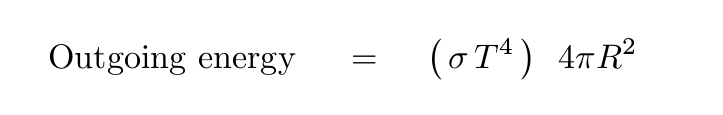
When the incoming and outgoing fluxes of energy are equal,

the planet will reach a steady equilibrium temperature T.
Q: Can you derive an equation for the equilibrium temperature T
of an object at orbital distance a from its host star?
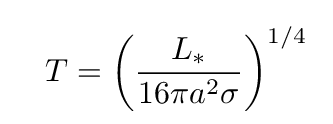
Some of the circumstellar disks we see stretch out away from their host star to distances larger than that of Neptune and Pluto from the Sun. In the HL Tau system, for example, we can detect emission from dust and gas well beyond 100 AU from the star.
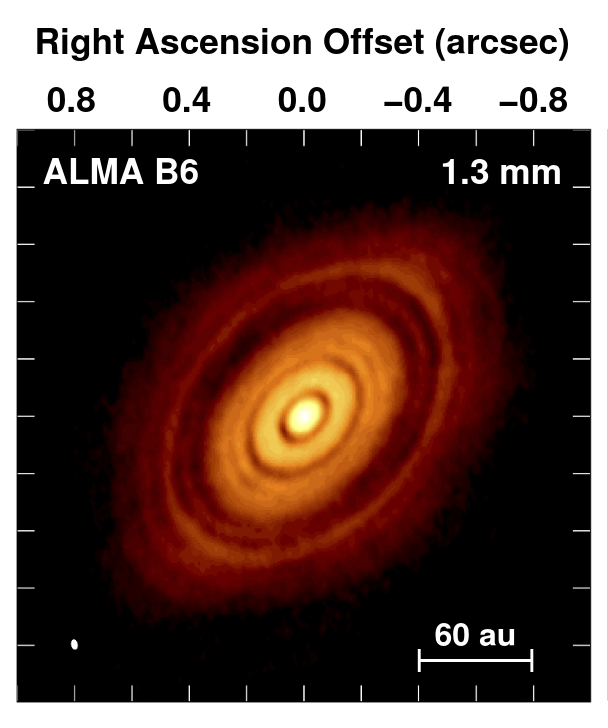
ALMA map of HL Tau taken from Figure 1 of
Carrasco-González et al., ApJ 883, 71 (2019)
What temperature would dust particles have at large distances from the star? The luminosity of HL Tau is roughly 11 times the solar luminosity (as stated in Liu et al., A&A 607, A74 (2017) ). Use the formula above to fill in the table below.
peak wavelength
Distance (AU) Distance (m) T (K) lambda (microns)
-----------------------------------------------------------------------
10
20
40
100
-----------------------------------------------------------------------
The results of our simple formula do a pretty darn good job of matching the observations:
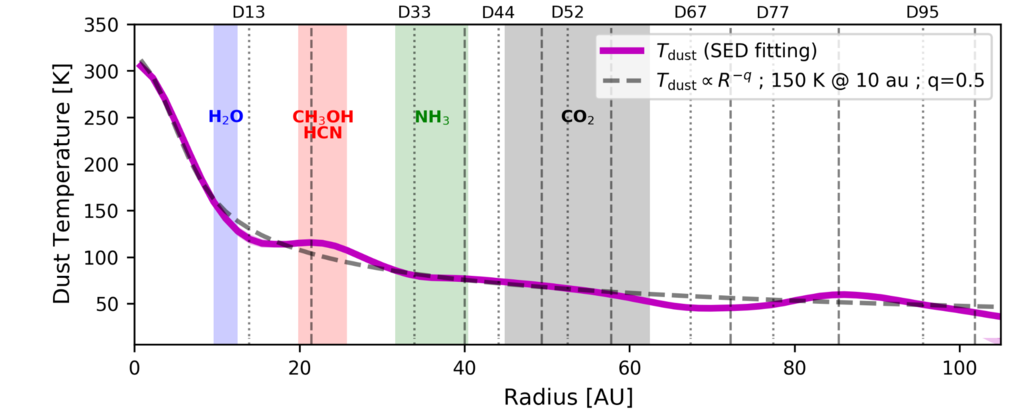
Taken from Figure 7 of
Liu et al., A&A 607, A74 (2017).
Q: What sort of telescope would be best suited for observing
circumstellar disks of this sort?
Q: Why? Give at least TWO reasons.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.