Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Our next few classes will be devoted to one big goal: using the physics of material inside stars to build a MODEL of a star inside a computer. Once we have an accurate model, we can use it to investigate the observed properties of stellar exteriors. If all goes well, we may be able to explain certain characterstics of these exteriors -- such as the correlation between luminosity and temperature along the main sequence.
Our model will make two big simplifying assumptions:
Both of these are good approximations for ordinary main-sequence stars like our Sun.
A good model, it turns out, will require 5 differential equations. Today, we'll deal with two of them, which describe the changes in MASS and PRESSURE as a function of radial position within a star.
How does the mass of a star change as we move from one position to another within its interior? This is actually pretty easy to answer -- you've probably seen the following reasoning and calculations in some other classes. Suppose that the star has a constant mass M and radius R, but a density ρ which may not be constant. In that case, we need to write the density as ρ(r).
Let's consider one thin little spherical shell, starting at radius r and extending outward by a small distance dr.
Q: What is the volume of this little shell? Q: What is the mass of this little shell?
Right.
In order to compute the total mass M of the star, we simply integrate over all shells, from the center to the surface.
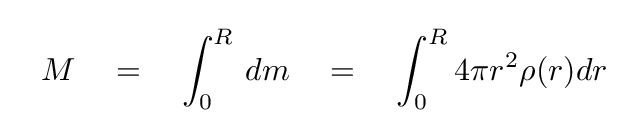
Let's do a simple example, just for practice. Suppose that a star has a radius R = 6.95 x 108 m, the same as that of the Sun -- nothing strange about that -- and a constant density ρ = 1000 kg/m3 -- which would be very strange indeed.
Well, since the density is constant in this case, we can pull it out of the integral, which is then easy to evaluate.
Q: What is the mass of this unusual star?
Right again.
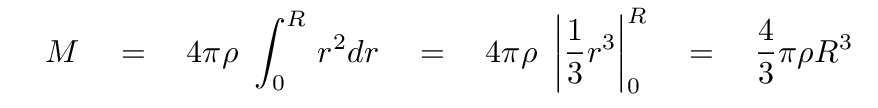
If one inserts the appropriate values for radius and density, one finds a mass of about M = 1.4 x 1030 kg ... which is pretty close to the mass of our real Sun. Hmmm. Evidently, the average density of material in the Sun is pretty close to that of water!
Now, the most useful form of this relationship between mass and density will be a differential one. If we define Mr as "the mass INTERIOR to a radius r", then we can re-arrange things a bit to yield one of the five key equations of stellar structure:
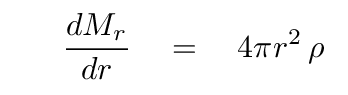
If our star is a static one, then each little piece of material must neither rise nor fall. Let's see what we can deduce from this simple fact.
Consider a little cylinder of gas at some radial distance r from the center of the star. The cylinder has top and bottom surfaces of area A, and a height dr. The cylinder is so small that we may treat the gas inside it as having a constant density ρ.
In a star with spherical symmetry, the forces due gas pushing on the sides of the cylinder will cancel each other. That means that there are three forces acting on the gas within the cylinder:
Q: How large is Ftop? Q: How large is Fbot? Q: How large is Fgrav?
The forces pushing on the top and bottom surfaces of the cylinder are equal to the pressure of the gas at each location, multiplied by the area of the top (or bottom) of the cylinder. The force of gravity depends on the mass of the gas inside the cylinder and the local acceleration due to gravity. We can write the sum of these forces as
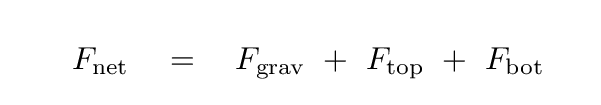
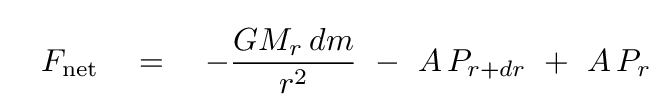
We can replace the mass inside the cylinder dm with the product of its volume and density.
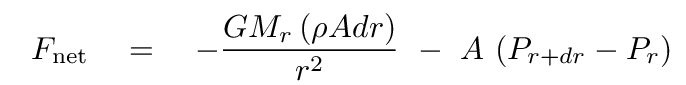
We can also re-write the difference in pressure between the top and bottom faces in terms of the change in pressure with radius, dP/dr.
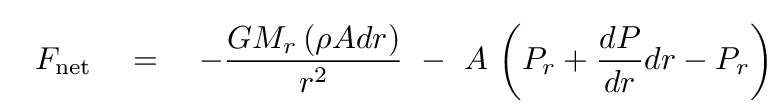
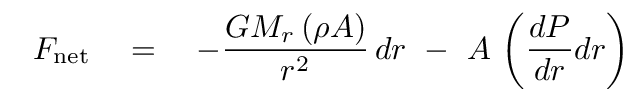
Finally, we divide both sides by the area A to find
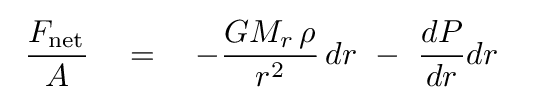
Q: If the star is in static equilibrium, what must the net
force on this cylinder be?
The answer, of course, is zero! So the left-hand side of the equation is zero. That allows us to solve for the pressure gradient dP/dr.
Q: Write an expression for dP/dr in terms of the other quantities.
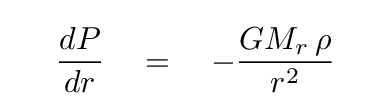
This is the second of the five differential equations we will need.
Let's try a quick and (very) dirty application of this equation. Suppose that we treat the differential equation (dealing with teeny-tiny slices of a star) as a difference equation (dealing with big chunks of a star). Let's pretend that the star has a constant density, and divide it into a single slice of size Δr = R running all the way from the center to the surface.
We can use values
Q: Assuming that the pressure at the surface is zero,
what is the pressure at the center of this star?
Q: How does that compare to the pressure of the air at the
Earth's surface?
So we have a differential equation for pressure: if we know the value pressure at one location, we can figure out the change in pressure as we move to a neighboring location. Fine. But how can we find the pressure of one location to serve as a starting point? Or, if we know the properties of one particular chunk of gas, is there any way to find the pressure RIGHT THERE?
What we need is a way to express the pressure in terms of other gas properties; in other words, we need an "equation of state." For the common case of an ideal gas, there is a simple equation of state:
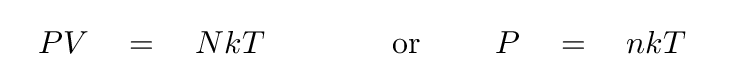
In the first form, N is the total number of particles in the volume V; in the second form, n is the number density of particles per unit volume.
Now, astronomers often use a slightly different form. We sometimes prefer to include the mass density ρ,
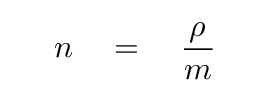
If there are a mix of particles -- say, protons and electrons, or hydrogen and helium atoms -- then we can define a mean particle mass
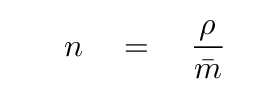
and then the ideal gas law turns into
Moreover, since hydrogen is so common in most astronomical situations, we define a special symbol μ to stand for the mean particle mass, in units of hydrogen masses:
This quantity μ is often called the mean molecular weight.
With all these special symbols, the ideal gas law can be written
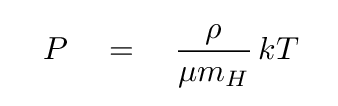
Finally, astronomers have devised one more set of symbols you may see in calculations for the state of gas in a star or cloud of gas in space. We sometimes describe the chemical composition of gas by breaking it up in three pieces: hydrogen, helium, and "everthing else" (also called "metals"). We describe each piece in the following manner:
Note that by definition, X + Y + Z = 1 .
In the Sun, and in most main-sequence stars, the gas pressure is usually the dominant contributor to the overall pressure. In some places within some stars, however, the pressure due to radiation can match or exceed that due to the particles of gas. Is there some way to compute the pressure in these situations?
Indeed there is. Carroll and Ostlie go through a nice derivation in Section 10.2, showing a general method one can use to compute the pressure of photons travelling through some parcel of gas. The end result will depend on the photons' distribution of energy and momentum, and so, in general, requires complex integrals.
However, there is one relatively common situation that yields a simple result. If the radiation field is that of a blackbody, then -- as we have seen before, the radiation pressure is
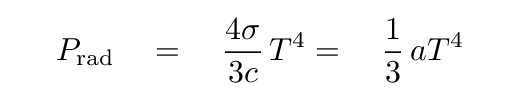
where
Let's try out our new equations to estimate conditions at the core of the Sun. One of the items we'll use in our calculations is the mean molecular weight, μ.
Q: What is a reasonable rough guess for the mean molecular weight μ
at the center of the Sun? (Hint: assume pure hydrogen)
A bit earlier today, we tried to estimate the gas pressure at the center of the Sun. We made a pretty bad starting assumption, so the value we derived was about 100 times smaller than the actual value. Let's throw away our bogus estimate and adopt that real value. We can then use this accurate gas pressure to estimate the temperature in the core of the Sun. Use this version of the equation
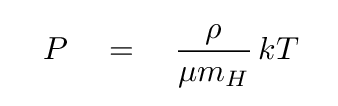
with the following values
Q: Can you re-arrange the equation to solve for temperature? Q: What is the temperature at the center of the Sun?
Great! Now that we have the temperature at the Sun's core, we can compute the radiation pressure there. We've assumed that the gas pressure is the dominant contributor -- but is it really? Let's see. Insert the temperature we just derived into this equation for radiation pressure.
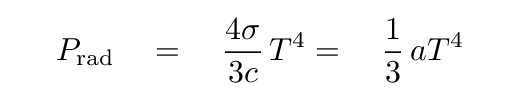
where
Q: What is the radiation pressure at the Sun's core? Q: How does it compare to the gas pressure? Q: Was our assumption that gas pressure dominates a good one?Q: What is the temperature at the center of the Sun?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.