 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
We have three differential equations describing how fundamental properties of a star -- mass, pressure, energy generation -- vary with radius. We need one more equation in order to build a good stellar model: how does temperature change with radius? Our method will be to consider the rate at which energy is transported within a star, from one thin little layer to the next.
As you may recall from first-year physics, there are three general methods to move energy from one place to another.
Since conduction requires very dense material, it turns out not to play any important role in ordinary main-sequence stars, so we'll just ignore it for now; though if we were studying white dwarfs or neutron stars, we'd definitely have to include it.
Radiation is the transfer of energy via the flow of photons in some direction. Convection moves energy from one place to another by the translation of big chunks of hot stuff from point A to point B. Each of these processes can dominate the energy flow in certain regions of main-sequence stars. Let's take them in order.
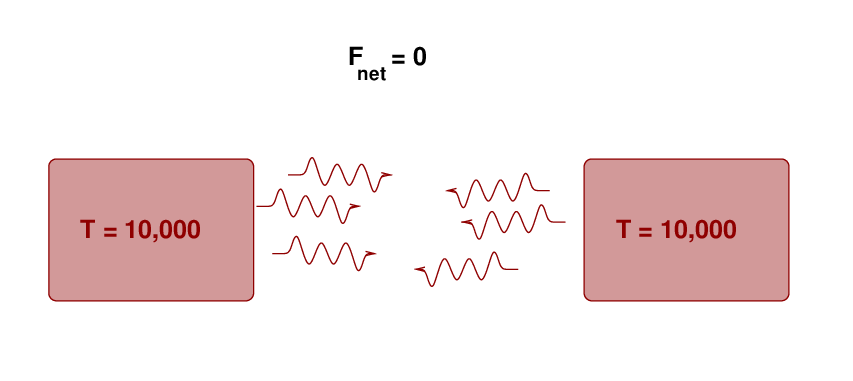
Imagine two chunks of gas which are identical in all respects, sitting next to each other. Each emits radiation and absorbs radiation from its neighbor -- but the inflows and outflows are equal. There is no net flux of radiation between them.

But if one of the two chunks is hotter than the other, then there WILL be a net flow of energy.
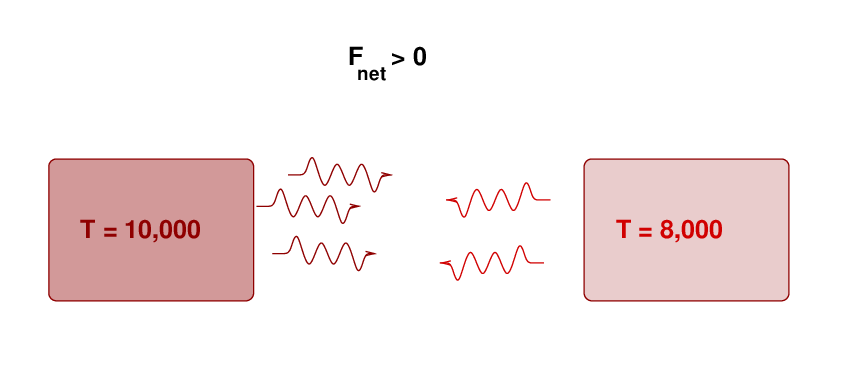
The flow of energy will occur across a boundary if the temperature of the gas is different on either side of the boundary (assuming all else is equal). So, it's reasonable to conclude that there will be a connection between the net flux of radiation Frad and the temperature gradient at that location dT/dr.
Let's dress this idea up with some math.
You may recall that the radiation pressure is related to temperature (for a blackbody) in the following way.
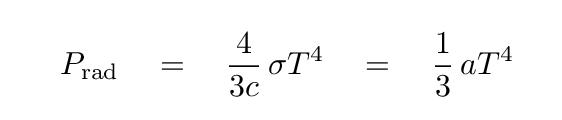
If we take the derivative of pressure with respect to radius in the star, we get an expression
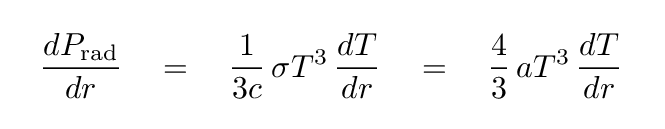
that involves a term with our goal -- dT/dr. Let's keep working to find a way to express the temperature gradient in terms of more basic quantities -- without another derivative.
It turns out that there is another way to write the radiation pressure gradient, one which depends upon the net flux of radiation through some boundary.
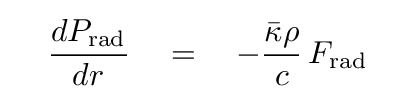
Q: Why is there a negative sign in this expression?
If the net flux flows from left to right, then that must mean that the radiation pressure is greater on the left than the right -- so the radiation pressure DECREASES in the direction that the flux is moving.
We can set these two expressions equal to each other.
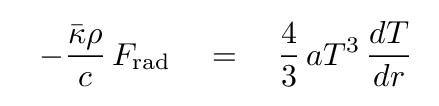
Now, for a simple, spherically symmetric star, the radiative flux at a radius r from the center is simply
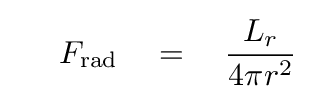
which means
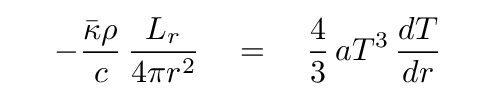
Q: Can you re-arrange to solve for dT/dr ?
You should end up with
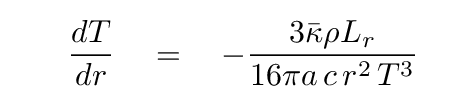
And there it is: our final required differential equation -- IF the energy is being moved via radiation. Some things to note:
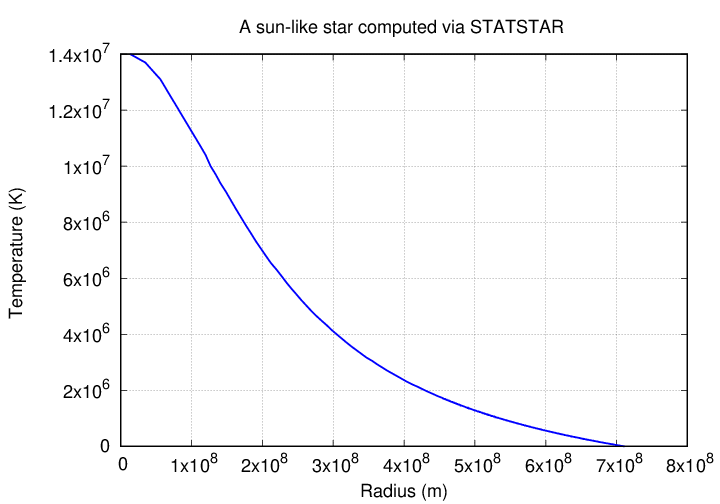
Let's try to use this equation to estimate the temperature gradient near the core of the Sun. We'll look just outside the region in which fusion is taking place, so not exactly at the very center.
Just outside the core of the Sun, the conditions are very roughly
T = 1.0 x 10^(7) K
Lr = 3.8 x 10^(26) J/s
rho = 2.0 x 10^(4) kg/m^3
kappa = 2.0 m^2/kg
r = 2.0 x 10^(8) m
Q: What is the temperature gradient at this location?
Q: If this temperature gradient remained constant all the way to
the surface of the Sun (it doesn't), how far from the center
would the temperature drop to zero?
How does that compare to the actual radius of the Sun?
We can compare your results to those from a proper stellar model, the STATSTAR program which is included in one of the Appendices of your textbook.
The other process which may be important in moving energy from place to place within a star is convection. Let's talk about the general idea here, and then move on to mathematics later.
Convection is basically like a conveyor belt running inside a star:
The cycle continuously brings energy from the interior to the outer layers of the star. Under some circumstances, convection can move energy much more rapidly than radiation. Our job is two-fold: first, figure out how the temperature will change with radius IF convection is the dominant mechanism. Second, find the condition under which convection WILL be the dominant mechanism.
So, consider a blob of gas which is initially (subscripts i) at some density and temperature, surrounded by material with its own initial density and temperature. Suppose that the blob happens to rise upward by a very small distance dr, into a region where the surroundings have some final density and temperature (subscripts f).
What are the properties of the blob after it has risen by dr? And what will happen to it in its new location -- will it continue to rise (spawning a convection cycle), or will it sink back a bit to its initial position (no convection).
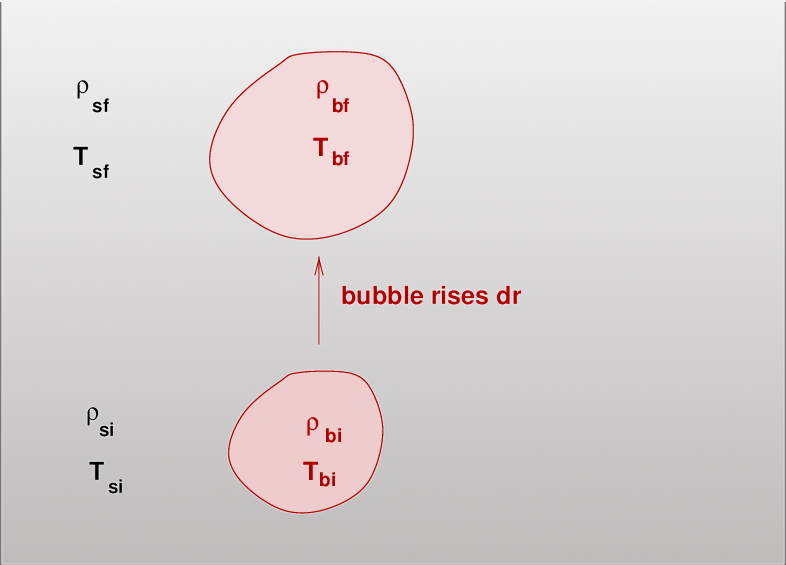
Our approach will be to assume that this tiny little motion happens quickly -- so quickly that the blob does not have time to exchange energy with the gas outside it. In other words, any changes in the blob must be adiabatic, which is a fancy word for "no energy leaks in or out". We will determine the new density (and temperature) of the blob after it has risen and expanded.
We will then compare the new density (and temperature) of the blob to the density (and temperature) of the surrounding material at the new location.
Now, the real goal here is to find an expression for the change in temperature with radius, dT/dr. So, as we go through this procedure, we'll have to switch from density to temperature. Fortunately, there is a decent approximation which makes that pretty easy: the ideal gas law. In the version below, the quantity m with a bar over it stands for "the average mass of a particle in the gas."
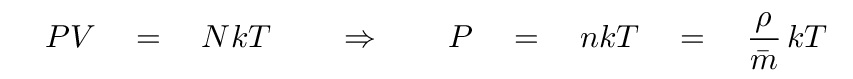
Since we'll be using the ideal gas law quite a bit, let's re-arrange it so that we can express any of the main quantities in terms of the others.
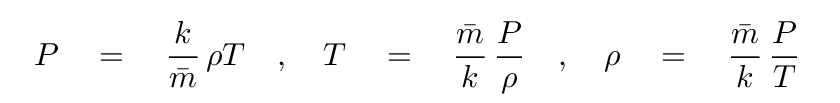
Suppose that our little blob of gas rises from its initial position by a distance dr. The pressure of the surroundings will change like so:
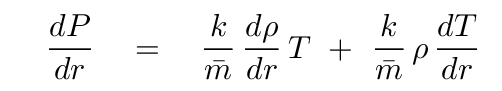
Aha! See the term for temperature gradient? That's a good sign. We can do a bit of algebra on this equation, using the relationships from the ideal gas law, to end up with a simple-ish expression.
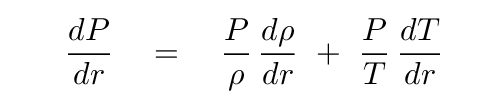
Okay. Now, we'll consider the gas inside the blob. As it has risen, it has expanded adiabatically. That means that there is a connection between the pressure inside the blob and its density
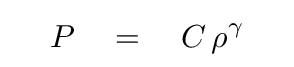
where γ is a constant that depends on the nature of the gas. For monatomic gases (like almost all of those inside a star), γ = 5/3. How does this pressure change with radius?
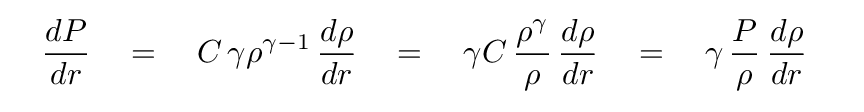
Now, if we assume that the pressure INSIDE the blob is always the same as the pressure OUTSIDE the blob, then the change in pressure inside and outside must be equal. That means we can write
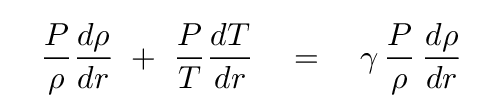
Q: Can you re-arrange this equation to solve for dT/dr ?
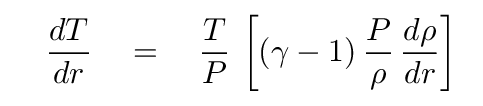
At this point, we must do a bit more algebra, using those relationships from the ideal gas law, to put the temperature gradient in one useful form:
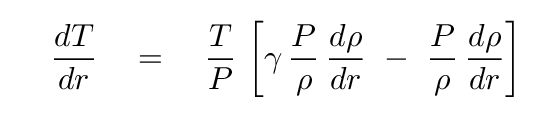
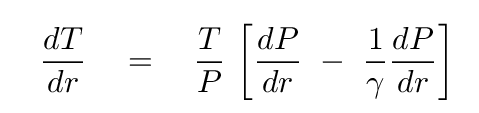
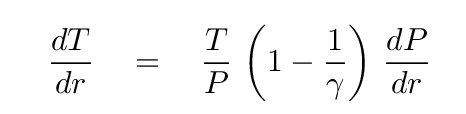
Okay. Phew. We are ALMOST finished. What we will do next is to take the first term on the right-hand side, and the last term on the right-hand side, and re-write them in slightly different ways. The FIRST term can be replaced with its equivalent from the ideal gas law, yielding a term with the reciprocal of density. The LAST term is the pressure gradient, dP/dr. But, wait a minute, we know that -- it was the second of the differential equations we derived in a previous lecture.
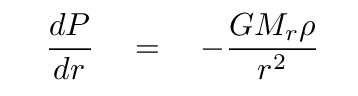
If we make those substitutions, and do a little MORE algebra, we end up with the differential equation for temperature as a function of radius IF convection is transporting the energy.
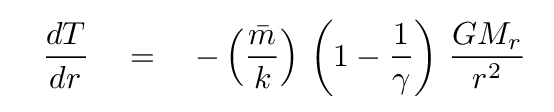
Note that this satisfies our hopes: it is a differential equation which only involves simple quantities (such as mass and radius), not other derivatives.
So we have one equation which is appropriate when radiation is the dominant mechanism, and a different equation which should be used when convection is the leading mechanism ... but how do we know which one to use?
The answer is pretty simple, thanks to one feature of convection: it is a very, very efficient way to move energy. If convection is operating, then the temperature gradient will be pretty darn close to the value we just derived. In other words, convection is so good at moving energy that it will prevent the temperature gradient from growing much larger than that theoretical value.
So, when building a model, check the absolute value of the actual temperature gradient in your model, and compare it to the absolute value of the gradient which would be produced by convection. If

then convection will be dominant, and one can (mostly) ignore radiation. On the other hand, if the absolute value of the actual temperature gradient is smaller than the absolute value of the adiabatic gradient, then radiation will dominate, and one can (mostly) ignore convection.
There is another way to write the condition for convection to occur; it's equivalent to the other, but simpler in some situations. It is especially convenient if one is examining the properties of some stellar model in a computer.
Suppose that the pressure and temperature of a star are related by a power law with some exponent α. If so, then the logarithm of pressure is just α times the logarithm of temperature.
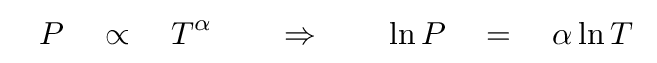
But another way to express this relationship is by taking the derivative of the logarithms:
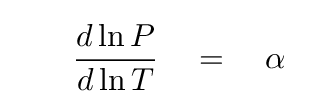
Recall for adiabatic expansion, the the factor γ, the "ratio of specific heats", was involved. It turns out that in adiabatic expansion, one can derive a simple power-law relationship between pressure and temperature, with an exponent which depends on this γ. Specifically,
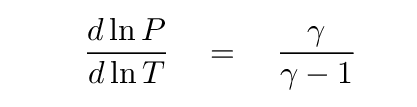
Q: If gamma = 5/3, then what is the value of this right-hand side?
Right. The right-hand side is equal to 2.5 in that case.
So, IF some region of the star is exactly adiabatic, then the logarithms of pressure and temperature will be related by this factor of 2.5, exactly, and convection will take place. And if the temperature gradient is even sharper, a condition known as "super-adiabatic", then convection will also take place. In other words, the condition for convection to dominate can be written as
IF
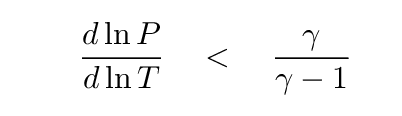
THEN convection is dominant.
Consider an example, again from the STATSTAR program. One model of a star sort of like the Sun shows this temperature profile

and this pressure profile
If we plot pressure vs. temperature, we get
But if we plot the LOGARITHM of pressure vs. the LOGARITHM of temperature,

Q: Is there any location in this stellar model where we might
expect convection to be active?
Look closely -- very closely -- at the regions with highest pressure and density; in other words, at the central regions of the star:
Aha! At the very center, in the innermost 8 or 9 layers of this stellar model, the slope of this pressure-temperature relationship is equal to 2.5. That means that only in these innermost layers is convection going to be active, and so only in these layers will we apply this equation to our stellar model:
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.