The center of mass in an extrasolar system

So, suppose that we point our telescopes towards some distant star. It is so bright, and any possible planets around it are so faint, that we can only detect the light of the star itself.

Rats.

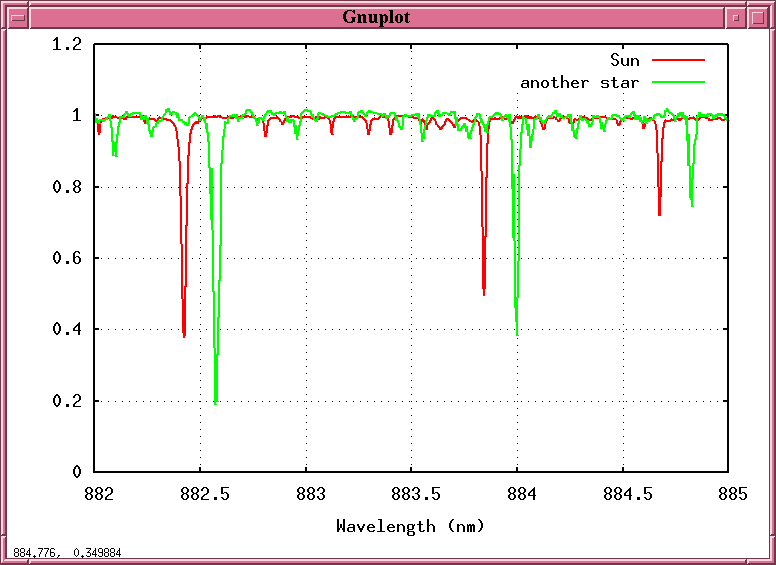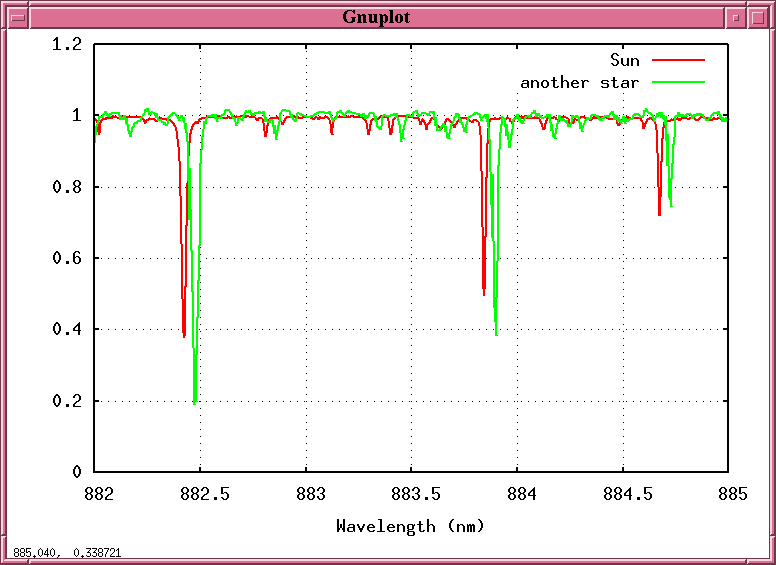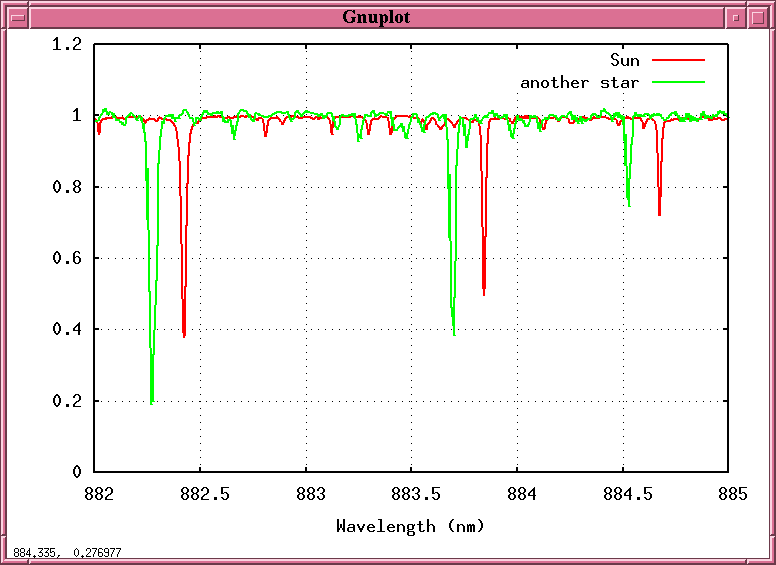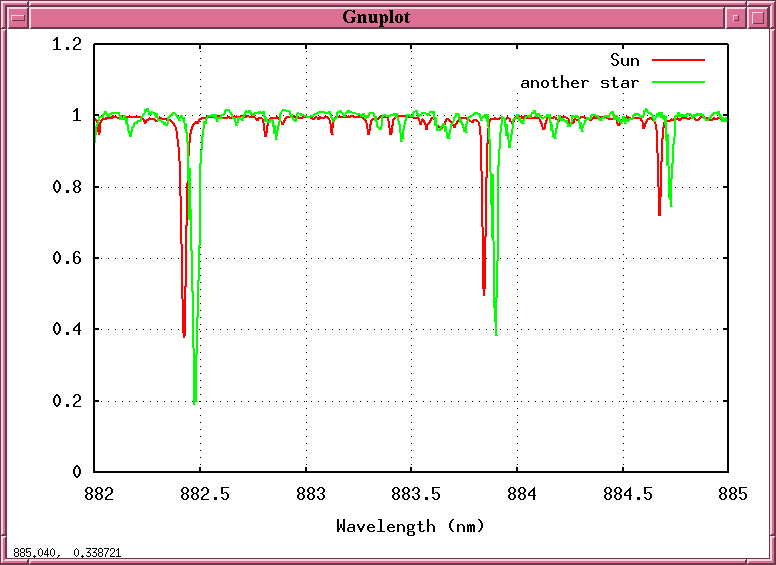
But suppose that we split this starlight into a spectrum and record it -- not just once, but over and over again, night after night, week after week. Maybe, just maybe, we might see the spectrum of that starlight change ....

  Q:  Why should the starlight shift back and forth, 
          back and forth, in a periodic fashion?









  A:  Because the star is moving towards us and 
          away from us, towards us and away from us,
          as it circles around the center of mass
          between it and a planet!

A little animation illustrating radial velocity curves

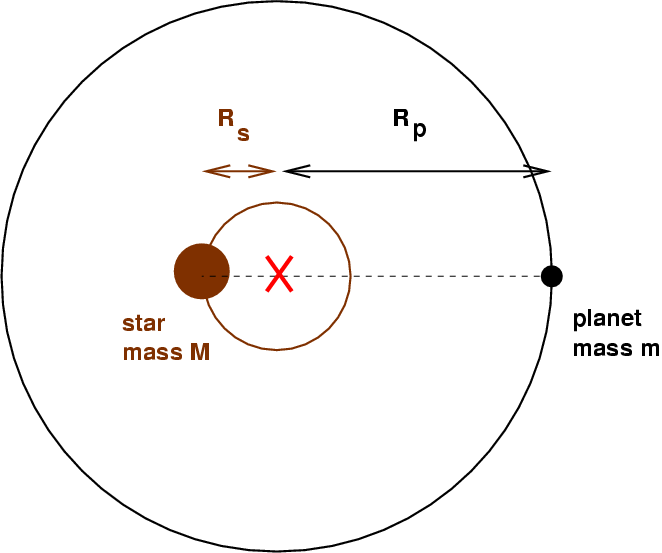
If you could figure out the size of the star's orbit, R_s, and if you knew the size of the planet's orbit R_p -- which is always much, much, larger -- then you could figure out the ratio of orbital radii, and, thanks to center of mass, the ratio of masses.

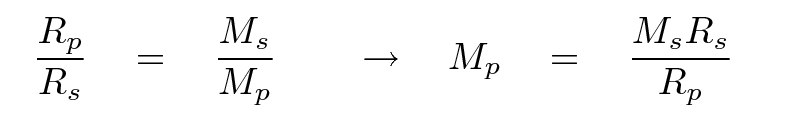
Look at the measurements of a star called "tau Bootes". This star is roughly the same mass as the Sun, so let's use M_s = 1.99 x 10³⁰ kg. Measurements of its spectrum show that the star moves in a circle with a period of P = 3.312 days and a speed of about v = 466 m/s.

1. What is the circumference of the star's orbit? In other words, how far does the star travel as it makes one complete circle?
2. What is the radius R_s of the star's orbit around the center of mass?

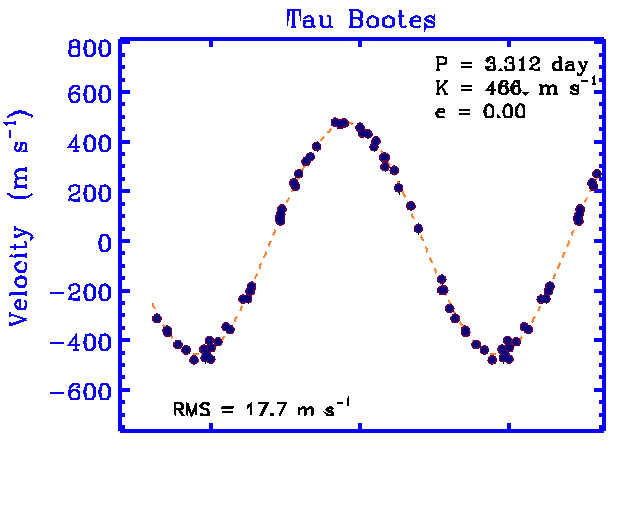
Now, the planet is circling the star with a much larger orbital radius R_p, but with exactly the same period P. How can we find its orbital radius? Let's assume that the star and the planet are both moving in perfectly circular paths. In that case, we can compute the star's centripetal accleration


3. What is the centipetal acceleration of the star?

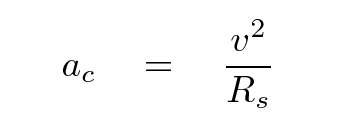
The acceleration is caused by the planet's gravitational force pulling on the star, so we could write



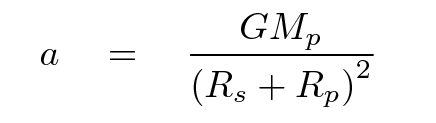
That leaves two unknown quantities, R_p and M_p, with just one equation. Fortunately, we have another equation relating these two properties of the planet, so we can substitute to end up with one equation for one unknown.

4. Substitute for the mass of the planet in the above equation for acceleration, leaving an equation which has acceleration on the left hand side and only one unknown, R_p, on the right-hand side.
   

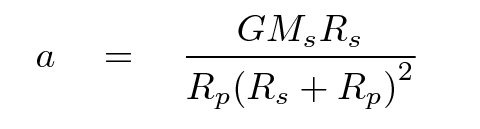
   Because stars are much, much more massive than planets, we can assume that the distance of the planet from the center of mass is much, much larger than the distance of the star from the center of mass.

   

   In other words,

   

5. Write an equation which shows the acceleration of the star on the left-hand side, and an approximated, simplified expression with only one unknown on the right-hand side.
   

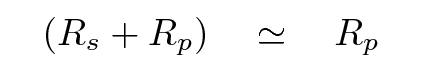
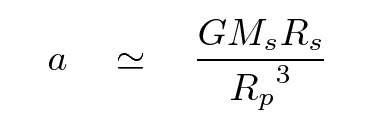
   Excellent!

   Now you can figure out the radius of its planet's orbit.

6. What is the radius of the planet's orbit around the star?
7. How does the planet's orbit compare in size of the orbit of the Earth around the Sun?
8. What is the mass of the planet?
9. How does the planet's mass compare to the mass of the Earth?
10. Would you like to live on this planet?

For more information

• Different methods for finding extrasolar planets from an introductory astronomy course.
• A few thoughts on life on the known extra-solar planets, ditto
• The extrasolar planets encyclopedia has up-to-date information.

Copyright © Michael Richmond. This work is licensed under a Creative Commons License.