How the period of an orbit is related to its size

There is a relationship between the size of a satellite's orbit around the Earth and the period of that orbit. Can you figure it out?

Write down an equation which connects the period P of an orbit to the speed v of the satellite.
Use that equation to derive a formula which gives the centripetal acceleration a of the satellite.
Now, suppose that the satellite has mass m and is at a distance R from the center of the Earth. Write down a general formula for the gravitational force on the satellite.
Derive a formula for the gravitational acceleration of the satellite.
Set the two accelerations equal to each other.
Re-arrange terms so that your equation looks something like this:
What are the powers "x" and "y" in your equation?
What is the "stuff" in your equation?

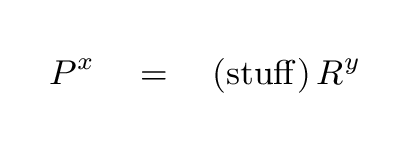
This relationship between the orbital period P and orbital radius R was first noticed and published by the German astronomer Johannes Kepler way back in 1619. It was one of his proudest achievements, and is now known as Kepler's Third Law.

Some of you may be wondering why this is such a big deal -- if you could figure it out in an hour or two, why couldn't Kepler, or any other astronomer of his day? Perhaps you don't realize that Newton's description of gravity hadn't been published yet; in fact, Newton wasn't born until 1643. Moreover, the kinematic and dynamic connections between forces, accelerations and velocities were not really worked out at this time....

This relationship isn't limited to motion around the Earth. You can use it for any situation in which a one body orbits a much more massive one (and, with a bit more work, use it even when the two bodies are of comparable mass).

Mercury orbits the Sun at a distance of about R = 58 million km. How long does it take to make one complete revolution? (You can check your answer in the textbook)
Europa, one of Jupiter's moons, takes about P = 3.55 days to circle Jupiter. What is its orbital radius?

For more information

A bit of history on transits of Venus includes some material on Kepler's achievement.
If you want to get into the gory details, look at lectures from my Stellar Astrophysics course starting with "Elliptical orbits" and ending with "Integrals of motion and Kepler's Third Law (again)".