Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
When a massive star runs out of fuel, its core collapses from the size of the Earth to a compact ball of neutrons just ten miles or so across. Material just outside the core falls onto this very hard, dense ball and rebounds outwards, sending a shock wave through the star's envelope. The shock wave heats the envelope to millions of degrees and throws it into space at speeds of over 10,000 kilometers per second.
But what happens to the super-dense core? It faces two possible fates:
We'll look at neutron stars today, and black holes a bit later in the course.
In ordinary matter, atomic nuclei are separated from each other by clouds of electrons which surround them.
If each nucleus were the size of a person, then they would be separated by about 100 kilometers. If YOU were a nucleus, your nearest neighbor would live in Buffalo.
Inside a white dwarf -- the core of an old, expired, low-mass star -- all the electrons have been stripped from individual atoms, so that electrons and nuclei mix freely. Since the nuclei are no longer protected by a cloud of electrons, they are now squished together so that they are closer by a factor of about 100.
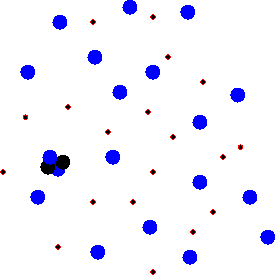
If YOU were a nucleus, your nearest neighbor would be somewhere on the other side of campus. You might even be able to see each other. But individual nuclei are still kept apart by innumerable electrons; they have no chance to interact directly.
Inside a collapsing core, the density and pressure become so large that electrons and protons are crushed together to form neutrons (and, as a byproduct, neutrinos):
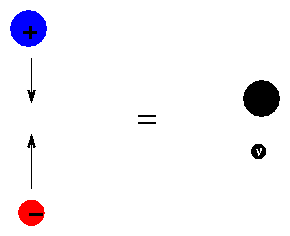
Neutrons can be packed very, very tightly together.
If YOU were a nucleus in a neutron star, your nearest neighbor would be standing right next to you, pressing up against you like people in a crowded subway car.
The density of a real neutron star reaches approximately 1015 grams per cubic centimeter.
In some (most?) supernovae, the neutron degeneracy pressure halts the collapse of the stellar core permanently. After the outer layers have expanded so far that they become transparent (which takes several years), one can look down into the center of the explosion and see a very small, very dense, VERY hot ball: a neutron star. For example, look at the Crab Nebula:
Near the center of the expanding cloud of gas is a star which is extremely blue, meaning it is very hot. We believe this is the neutron star created in the supernova explosion seen in 1054.
If we look carefully at the neutron star in the Crab Nebula with optical telescopes, we see that it blinks on and off, 30 times each second. The sequence of images below shows the two objects near the center of the Crab Nebula at intervals of (effectively) 1/240 second, or one-eighth of the rotational period.
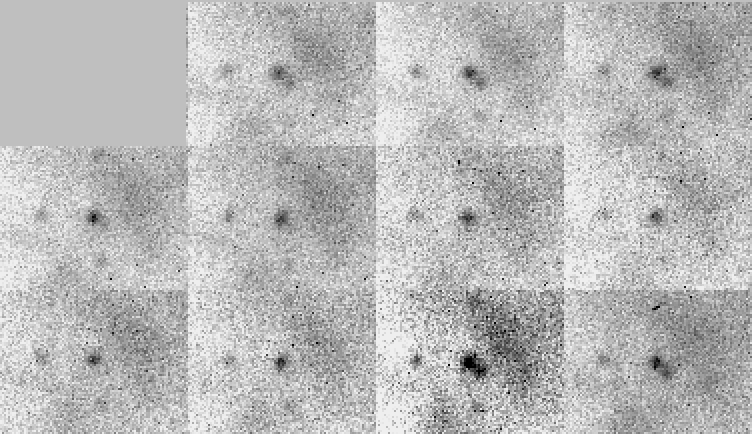
Read the full details of the observations.
Here's another view of the change in the pulsar's optical brightness as it rotates. This sequence looks better because it was taken with a much larger telescope, 4 meters in diameter versus 0.75 meters in diameter.
Image courtesy of Nigel Sharp/NOAO/AURA/NSF
The neutron star is spinning rapidly, due to the conservation of angular momentum. Angular momentum is a quantity which combines mass, size, and speed of rotation:
2
angular momentum = (mass) * (radius) * (rotation speed)
Before it collapsed, the star rotated relatively slowly, like our Sun: maybe once every five or ten days. But as it collapsed, the material retained its original angular momentum. The mass remained nearly the same, but the radius shrank; in order to compensate, the speed of rotation had to increase. If you set the original angular momentum to the final angular momentum, you can calculate the neutron star's rotational speed. It turns out the period of rotation after the collapse is
2
( size after )
period afterwards = period before * ( ----------- )
( size before )
So, for example, the Sun currently rotates with a period of about a month, and is very roughly 100 times the radius of the Earth. If the Sun were to shrink to the Earth's size, it would rotate with a period of one ten-thousandth = (1/100)2 of a month: that's only about four minutes!
Q: If the Sun were to shrink to the size
of a neutron star, about 10 km in radius,
how fast would it rotate?
Why does a neutron star flash as it rotates? Just as the angular momentum of a star is conserved as it shrinks -- causing it to rotate faster -- the original magnetic field of a star is conserved as it shrinks -- causing it to become extremely strong near the surface. On the Earth, the magnetic field is aligned with the rotational axis, so that the magnetic poles barely move as the planet rotates.
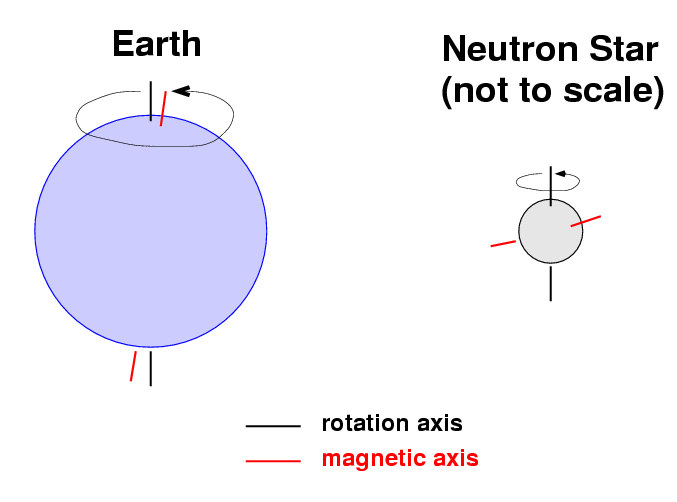
In some neutron stars, the magnetic field is NOT aligned with the axis of rotation. As a result, the magnetic field rotates together with the neutron star, very rapidly; as it rotates, it pulls charged particles along with it. The charged particles radiate light of all wavelengths -- visible, X-ray, and especially radio -- as they are pulled around and around and around. The result is a sort of magnetic lighthouse, which flashes in our direction twice each cycle. We call a neutron star which flashes in this manner a pulsar.
As the pulsar rotates, its radio beams sweep through the universe light a lighthouse. If you point a radio telescope at a pulsar and hook the receiver to an ordinary amplifier and speaker, you can listen to the pulses.
Some of the rotational energy of the pulsar is radiated away by the charged particles it sweeps around it; some of the energy is spent pushing wisps of gas outwards. Click on the X-ray image of the Crab pulsar below to see a movie showing its effect on the inner regions of the Nebula over a period of several months.
A pulsar's spin rate gradually decreases as it transfers energy to the material surrounding it. Radio astronomers have been able to measure very precisely the periods of many pulsars, and they can see most of them slowing down bit by bit. Below is a graph showing the measured frequency (rotations per second) of the pulsar called PSF 0833-45.
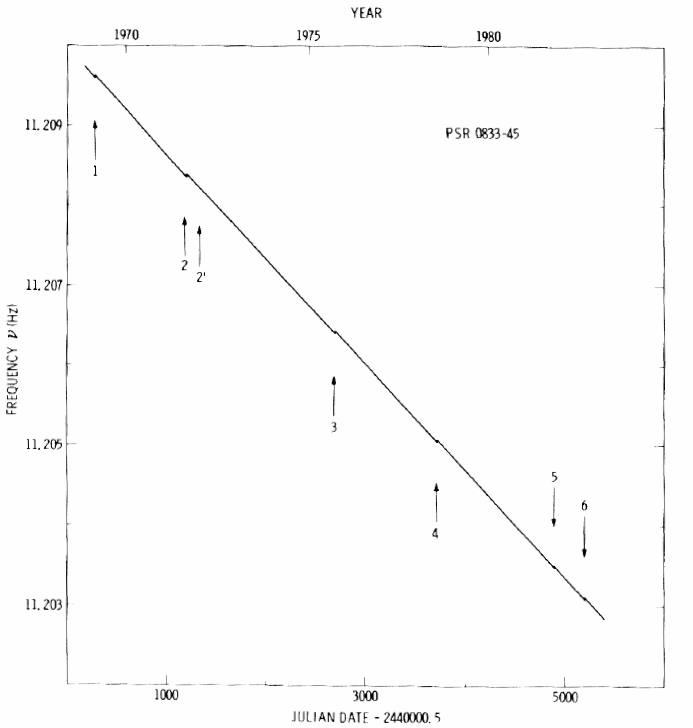
Q: Can you estimate how long it will take for
the rotation rate of pulsar PSR 0833-45 to
reach half its present value?
Over several million years, the neutron star spins down to the point that it can't accelerate enough charged particles to radiate a detectable amount of energy. It then becomes "invisible", and continues to spin slower and slower. Eventually, hundreds of millions of years later, it will be a simple ball of neutrons floating through space.
Even an isolated neutron star grabs one's attention, sending beams of radiation through the universe. But neutron stars with companions can be even more interesting if they are close enough to undergo mass transfer.
Imagine two stars which form together.
If one of them is very massive, it will burn through its fuel rapidly, become a red giant
and explode as a supernova,
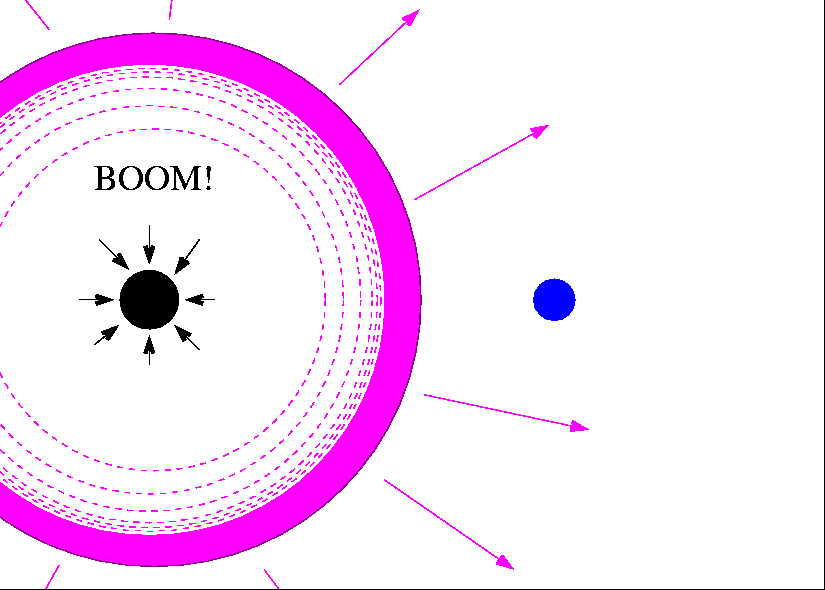
leaving behind a neutron star.
Eventually, the less massive member of the pair will also run out of hydrogen in its core, and begin to expand into a red giant.
As it expands, it blows some material off its surface into space. Some of that material is captured by the gravitational pull of the neutron star. If the companion grows large enough, the neutron star may even grab gas directly from the outer layers of the red giant:
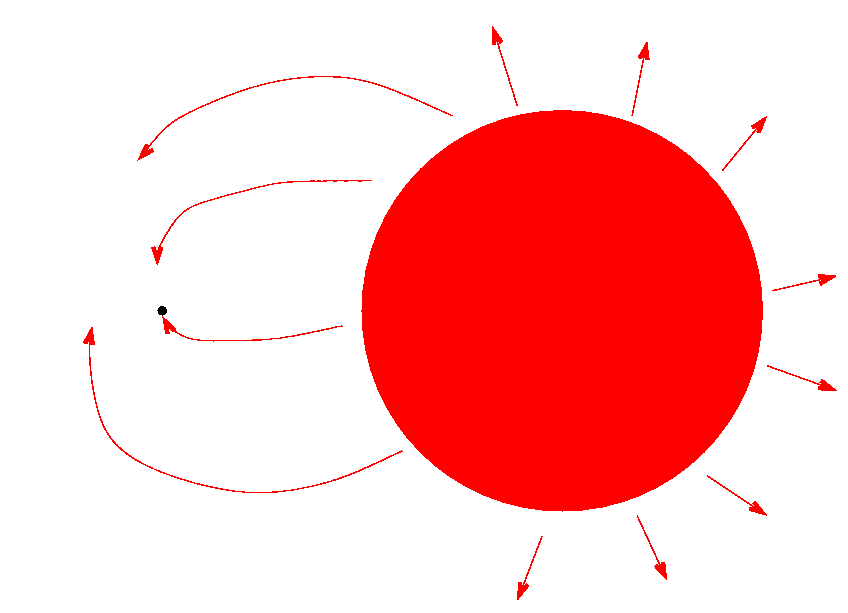
When material falls towards the neutron star, it doesn't fall straight downwards. Instead, because the two stars are orbiting around each other, the infalling gas spirals into an accretion disk around the neutron star.
Here's a movie showing a computer simulation of material falling inwards from the companion towards the neutron star:
This animation depicts an X-ray binary system consisting of a neutron star and a supergiant star. The neutron star is very dense, about 10 kilometers (6 miles) in diameter with the mass of 1.5 Suns. The supergiant companion star is about 7 times larger and 15 times more massive than our Sun. The neutron star has a massive gravitational pull, causing the winds from the companion star to be violently pulled into the neutron star. The result is a swirling mess of material in the stellar system, demonstrating the harsh environment produced by the strong gravitational force from the neutron star.
Gas in the disk spirals inwards, moving faster and faster and faster as it gets closer to the neutron star. Collisions between individual atoms as they orbit around and around heat up the gas. The material near the center can reach temperatures of hundreds of thousands, or millions of degrees, while the gas farther out remains relatively cool. The disk as a whole radiates energy at a very wide range of wavelengths.
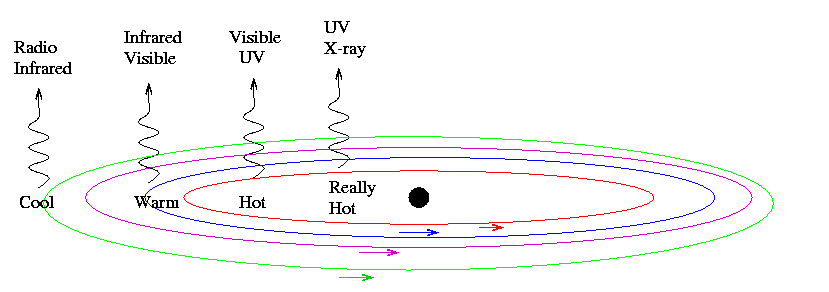
When we look at the sky with X-ray telescopes, some of the brightest sources are these X-ray binary systems. For example, the view of the Andromeda Galaxy at X-ray wavelengths shows many individual "hot spots" scattered throughout its disk.
Each one of these bright spots is a binary system in which a neutron star is accreting material from its companion.
Image credits: infrared: ESA/Herschel/PACS/SPIRE/J. Fritz, U. Gent;
X-ray: ESA/XMM-Newton/EPIC/W. Pietsch, MPE; optical: R. Gendler
Did you know there's a story about one man's encounter with
a neutron star?
Neutron Star, by Larry Niven
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.