Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Homework due in tomorrow's class
Astronomers at the Harvard College Observatory divided stellar spectra into classes: O, B, A, F, G, K, M. The major difference between stars in each class is temperature: the scale runs from hot to cool.
But are there other differences? The pattern of absorption lines changes greatly from class O to class M; is that due to a change in the chemical composition of the stars? For example, the Balmer lines produced by hydrogen are very strong in A and B stars, and virtually abset in K and M stars. Does that mean that the hotter stars have lots of hydrogen and the cooler stars very little?
Determining the chemical composition of a star from its spectrum turns out to be quite a tricky business. It took the astronomical community about three decades to figure it out. Let's see why ...
We'll begin by reviewing the conditions under which absorption lines are created in stellar spectra. Very dense, hot material in the inner regions of a star produces a bright continuum spectrum with light of all wavelengths. As the photons fly outwards into space, some are absorbed by atoms in the cooler outer layers of the stellar atmosphere, called the photosphere.
If we see an absorption line due to some element, we can be sure that there are some atoms of that element in the photosphere. But is the converse true? That is, if we do NOT see absorption lines due to a particular element, does that mean that atoms of that element MUST NOT exist in the photosphere?
No. It is not that simple, alas.
Well, what about the strength of a line? In the figure below, look at the strength of the Balmer lines of hydrogen at 410.1 and 433.9 nm:
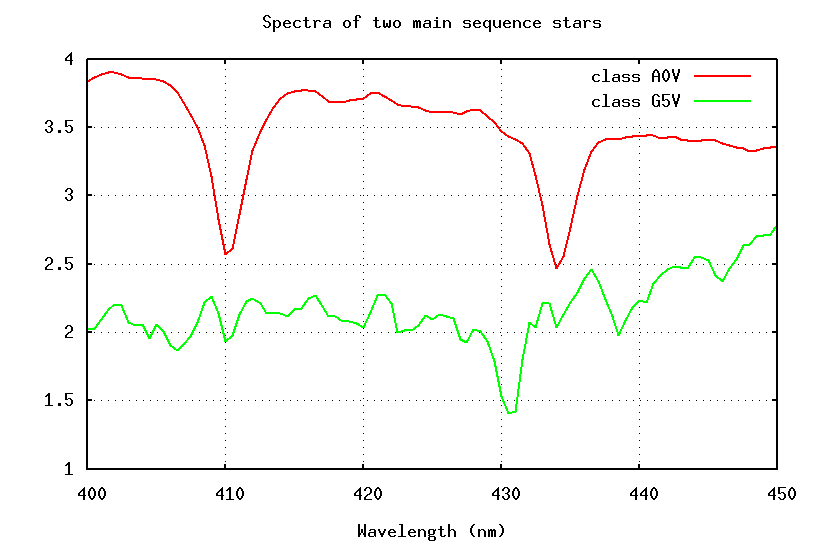
These absorption lines are much stronger in the spectrum of the A5 star; does that mean that there is more hydrogen in the photosphere of the A5 star?
Again, no.
Gosh. Why ISN'T there any simple relationship between the strength of a line and the abundance of its species?
Each species of atom or ion has a set of discrete energy levels. Neutral hydrogen, for example, has the following levels:
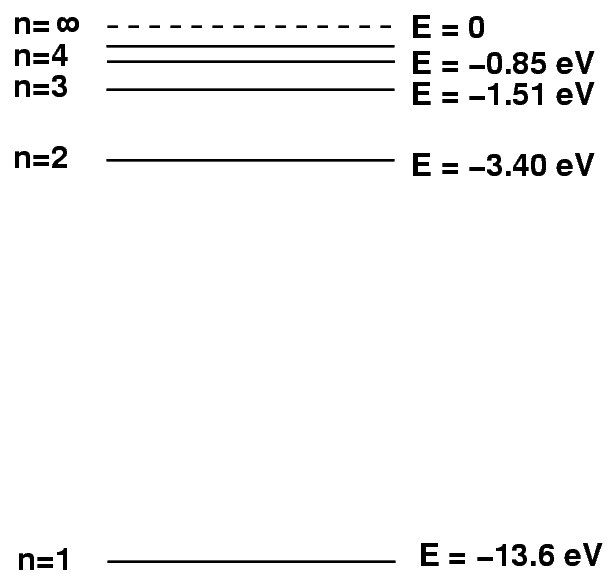
Atoms can absorb light only if the energy of the photon exactly matches the difference between their current energy value and a higher level. So, for example, if a hydrogen atom happens to be in the n=2 excited state, and a photon of energy E = 2.55 eV and wavelength 486 nm passes by, then the atom will absorb the photon and hop up into the n=4 state.
This transition will remove photons of wavelength 486 nm from the star's spectrum; we will see an absorption line at this wavelength, which we call the "Balmer beta" or "hydrogen beta" line.
However, if a hydrogen atom is NOT in the proper n=2 state, then this absorption will not occur. For example, if the atom is in its ground state, n=1, then any photon with less than 10.2 eV will pass right through it unaffected.
Likewise, if the hydrogen atom initially is in a state higher than n=2, it will again be unable to absorb the photon.
So, in order to produce an absorption line, two conditions must be met:
We ought to see very strong Balmer absorption lines in the spectrum of a star if a large fraction of its hydrogen atoms are in the n=2 energy state. Fine. But what is the connection between energy state and temperature?
It turns out an atom's energy state does depend on the temperature of the matter surrounding it ... but in a somewhat complicated way.
Under certain conditions, we can use the Boltzmann equation to calculate the relative number of atoms of a particular type in different energy levels.
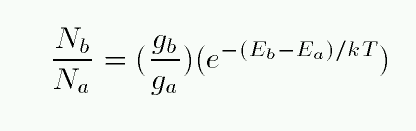
Note the two terms on the right-hand side. The first term includes factors describing the degeneracy of each energy level. In a hydrogen atom, there are g = 2 ways that an atom can exist at the n=1 energy level, and g = 8 ways that an atom can arrange itself at the n=2 energy state. Calculating degeneracies for hydrogen is easy, and you can look up the values for more complex atoms.
The second factor on the right-hand side depends on two quantities: the difference in energy between the two states, and the temperature T of the gas within which the atom sits.
Let's do just a simple calculation: assuming that this equation is appropriate for a stellar atmosphere, at what temperature T should the number of hydrogen atoms in the excited state n=2 just equal the number of atoms in the ground state n=1? All we have to do is re-arrange the Boltzmann equation to solve for temperature. You can look at the algebra if you want, but the result is:
Q: What is the temperature T at which
one might expect the number of hydrogen
atoms in the n=2 state to equal the number
of atoms in the ground state?
Um, gee, that sounds pretty hot. And if we go back to look at the spectral sequence, we see that ordinary stars with very strong Balmer lines are far below this temperature.
Something seems rotten; is there some physical fact that we are forgetting?
Yes, we are forgetting one critical fact: adding energy to a hydrogen atom will boost it from the ground state to an excited state, from which it may produce Balmer absorption lines; that's good.
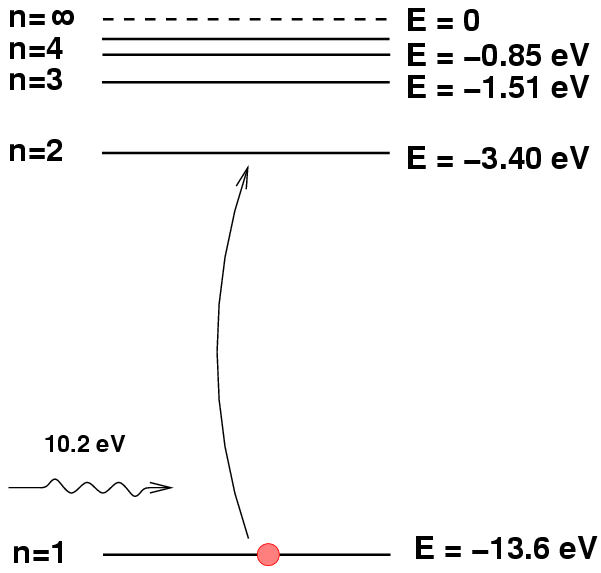
But adding just a bit more energy can eject the electron from the atom, leaving it unable to produce any absorption lines; that's bad.
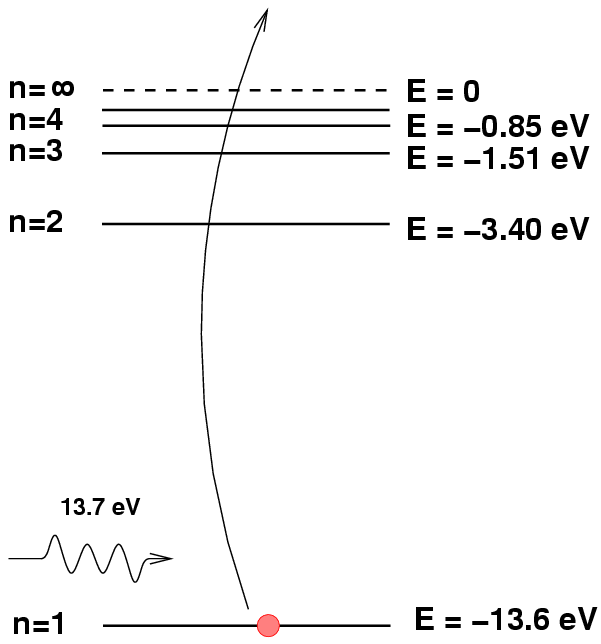
Atoms which have lost all their electrons are called ionized. Ionized hydrogen does not produce discrete absorption lines.
As the temperature rises in a gas, the atoms move more rapidly and collide more violently. So, as the temperature rises, atoms are more likely to be excited from the ground state n=1 to the state n=2, but they are ALSO more likely to be ionized. Indian astrophysicist Meghnad Saha figured out a way to calculate the fraction of atoms which are ionized (II) versus neutral (I) as a function of the temperature and the density.
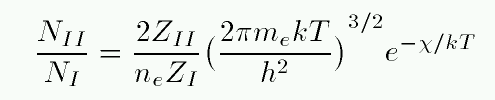
When one applies the Saha equation to hydrogen, one finds that the temperature required to ionize most of the atoms is surprisingly low: between 8000 and 12000 Kelvin, the gas changes from mostly neutral to mostly ionized.
So, producing strong Balmer lines is like producing good porridge.
This illustration by Arthur Rackham
was published in English Fairy Tales, by Flora Annie Steel,
(New York: Macmillan Company, 1918).
Using the Boltzmann equation, we can compute the fraction of hydrogen atoms which are excited into n=2, and using the Saha equation, we can compute the fraction which are lost to ionization. If we put the two effects together, we can figure out the temperature which is JUST RIGHT to place the maximum fraction of hydrogen atoms in the right state to absorb Balmer photons.
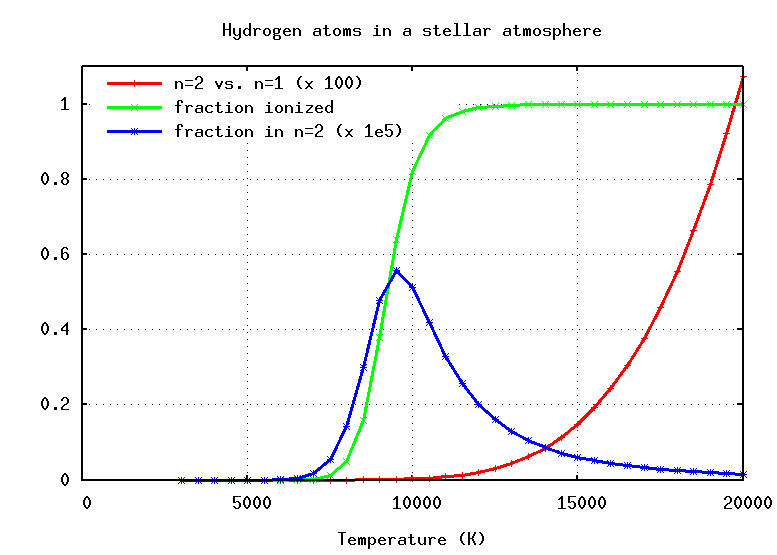
So, let's go back to the sequence of stellar spectra and look at the strength of the hydrogen Balmer absorption lines again.
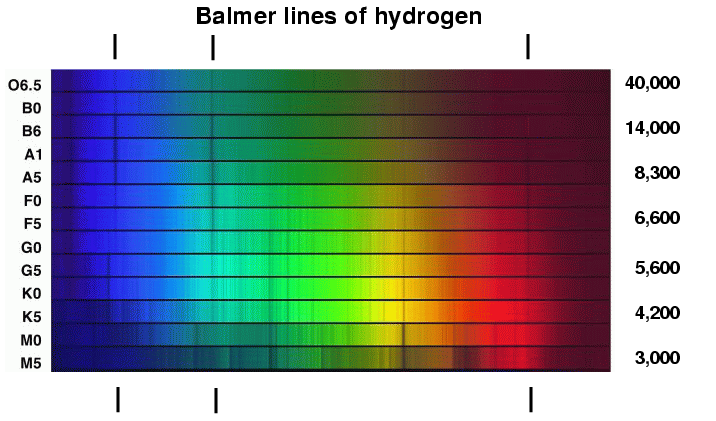
Q: Why are the lines weak in O stars? Q: Why are the lines strong in A stars? Q: Why are the lines weak in K stars?
The strength of the hydrogen Balmer lines in stellar spectra turns out to tell us a lot about the temperature of the stars ... but not very much, at first glance, about the amount of hydrogen in the stars. Figuring out the details of the chemical composition of a stellar atmosphere is a very hard task, and it involves a LOT more work than one might imagine.
Astronomers did not realize this at first, and for several decades, they concluded that the most common elements in stars were the ones which showed the strongest absorption lines: for example, since iron lines are so common in the solar spectrum, iron must be very abundant in the solar atmosphere. The turning point came in 1925, when Harvard graduate student Cecilia Payne synthesized the basic steps in her dissertation, Stellar Atmospheres: A contribution to the observational study of high temperature in the reversing layer of stars.
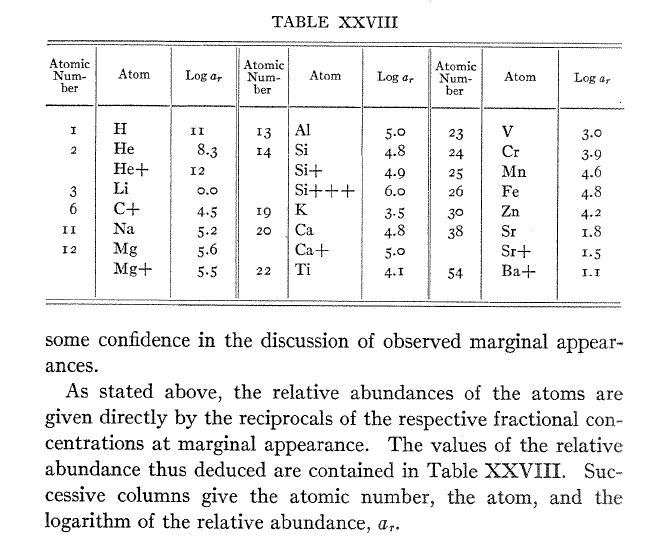
Table XXVIII from Chapter 8 of Cecilia Payne's dissertation.
Her conclusion that the most common elements in stellar atmospheres were hydrogen and helium was so surprising -- and so counter to the prevailing views of the day -- that it took several years for the astronomical community to accept her methods. Her thesis advisor, Harlow Shapley, wrote in the foreward to the published version of her dissertation
But we know now that she was correct.
Eighty years after Payne's dissertation, astronomers have a pretty good idea of the chemical composition of some stars. Let's look at the Sun, and compare it to the Earth.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.