The Saha Equation

We seem to have hit a roadblock. When we include atomic physics in our calculations, it seems that the Balmer lines should grow stronger and stronger as stars grow hotter and hotter. But the observations show that the Balmer lines decrease in strength at temperatures beyond 10,000 Kelvin. What's going on?

The problem isn't the atomic physics, per se. It's that we simply haven't included enough atomic physics. The Boltzmann equation tells us about the relative populations of a given species of atom: neutral hydrogen is one species, ionized hydrogen is a second, singly-ionized calcium is a third. What we have not YET considered is the interaction between species.

The missing piece: ionization?

Our calculations yesterday assumed that all the hydrogen atoms in a star's photosphere were neutral; or, more accurately, it provided the ratio of neutral atoms in the n=2 state to the n=1 state. But what if the number of neutral atoms changes drastically from A stars to B stars? That might cause there to be many more neutral atoms in the n=2 state in an A star, even if its temperature is lower than that of a B star.

Hmmmm. How to find the fraction of H atoms which are neutral? As a very rough first try, we might say, "When the temperature rises high enough that the typical kinetic energy of atoms reaches the energy required to ionize a hydrogen atom, then the material becomes ionized." In other words,

Exercise:

At what temperature will the "typical" collision cause a hydrogen atom to be ionized from its ground state?
How does that compare to the temperature of A and B stars?

Well, that doesn't seem to explain the situation with A and B stars, does it?

The partition function

Hold on a moment -- that calculation shows that stars must be REALLY hot in order for a collision to ionize a hydrogen atom in its ground state. But what about atoms in excited states? The first excited level, n=2, is more than halfway from the ground state to the ionization energy. If we include atoms of all levels in the calculations, we might discover that even stars with relatively low temperatures can ionize most of the hydrogen in their photospheres.

In order to do this calculation properly, we need to form a weighted average of the fraction of neutral atoms in each energy state.

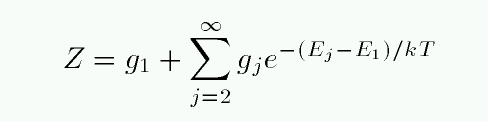
If we can form the partition function of all hydrogen atoms in the neutral stage -- call that Z_I -- and the partition function of all hydrogen atoms in the ionized stage -- call that Z_II -- then we can use the Saha equation to compute the relative number of atoms in each ionization stage.

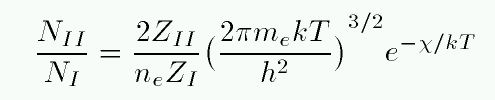
In this equation, n_e is the number density of free electrons, and χ is the energy required to ionize a hydrogen atom from its ground state.

Exercise: How does the ionized fraction of hydrogen depend on the density of free electrons? Can you explain this?

At temperatures of ordinary stars, kT is much less than 10.2 eV, the energy required to excite a hydrogen atom from the n=1 to n=2 state. Almost all neutral H atoms are in the ground state, so Z_I is very nearly 1. An ionized H atom has no energy states, so by definition, Z_II is exactly 1. That makes the calculation simple...

Material in ordinary stellar atmospheres obeys the ideal gas law, so one can replace the density of free electrons with a value involving the pressure of the free electrons and temperature.

Exercise:

Write down the ideal gas law, in the form involving k.
Rearrange this law to put density n on the left-hand side, and everything else on the right.
Rewrite the Saha equation, using your formula to replace the density of free electrons n_e with other quantities.
Use your formula to calculate the ratio of ionized to neutral hydrogen in a star with electron pressure P_e = 200 dyne per sq. cm.. Pick temperatures of 3000, 5000, 8000, 11000 Kelvin.

Putting it all together

Okay, let's consider a very simple model of a stellar atmosphere:

pure hydrogen
in thermodynamic equilibrium
consider only neutral atoms in n=1 or n=2, or ionized atoms

Call the number of neutral atoms in the n=1 state N₁, the number of neutral atoms in the n=2 state N₂, and the number of ionized atoms N_i. In order to absorb light and create the Balmer absorption lines, there must be lots of hydrogen atoms in the n=2 state. We can calculate the fraction of all atoms in this state like so:

first, find the fraction of all atoms which are neutral
then, find the fraction of all neutral atoms which are in n=2 (instead of n=1)

Exercise: For stars of temperature 3000, 5000, 8000, 11000 Kelvin,

what fraction of all hydrogen atoms are neutral?
what fraction of neutral hydrogen atoms are in the n=2 state?
what fraction of all hydrogen atoms are in the n=2 state?
Which star should have the strongest Balmer absorption lines?

When you have finished your calculations, compare the results to those in the textbook, or here:

For more information

How did Saha come up with his equation? Read his own words on the subject