
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
When a massive star runs out of fuel, its core collapses from the size of the Earth to a compact ball of neutrons just ten miles or so across. Material just outside the core falls onto this very hard, dense ball and rebounds outwards, sending a shock wave through the star's envelope. The shock wave heats the envelope to millions of degrees and throws it into space at speeds of over 10,000 kilometers per second.
But what happens to the super-dense core? It faces two possible fates:
We covered the first possibility last lecture. Today, let's look at the second one.
But what if the core is more massive? What if the core contains five, or six, or ten solar masses of material when it collapses?
If that's the case, then there is nothing strong enough to resist the pull of gravity. Material falls inward, and inward, and inward, and just keeps falling. As it becomes denser and denser, the gravitational force pulling it in further increases without limit. What happens as the distance between adjacent particles R goes to zero?
G * m1 * m2
grav force = --------------
R^2
Mathematically, dividing by zero yields a singularity, a place where the oridinary rules don't apply. The center of a very massive stellar core apparently collapses into such a singularity. What does it look like?
We don't know.
Why not? Because we can't SEE the singularity.
When you throw a ball up in the air, it will always come back down. The gravitational force between the Earth and ball pulls it back. You can't throw a ball up far enough to alter the gravitational force on it significantly.

If you could throw a ball upwards really fast, say, at 10,000 miles per hour, it would travel far enough upwards (a large fraction of the Earth's radius R) that the gravitational force between it and the Earth would diminish significantly near the apex of its trajectory.
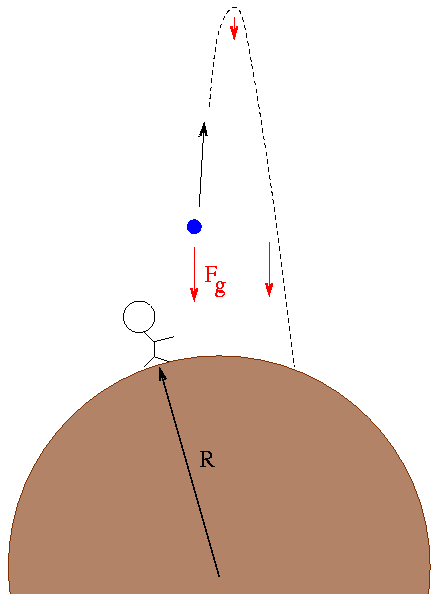
The gravitational force between the Earth and the ball decreases quickly once the distance between them doubles, or triples. It turns out that if you can throw the ball upwards fast enough, you can cause it to move upwards, away from the Earth, forever:

The critical speed at which the ball will continue to move away from the Earth forever, and never come back, is called the escape velocity. You can calculate it by this formula:
[ 2 * G * M ]
escape velocity = sqrt [ ------------ ]
[ R ]
where
G = 6.67 x 10^(-11) is the universal gravitational constant
M is the mass of the planet (or star) in kg
R is the radius of the planet (or star) in m
The formula will yield the minimum speed, in meters per second, with which one must throw a ball upwards from the surface in order to cause it to recede forever.
Q: What is the escape velocity from the Earth?
It's not easy to reach such high speeds. In Jules Verne's novel From the Earth to the Moon, the Baltimore Gun Club builds a REALLY big cannon to send a shell to the Moon.
The Sun's mass gives it a much higher escape velocity than the Earth: about 620 km/sec.
But what happens if an object's mass is really big, but its size is really small? That will make the escape velocity very large. In fact, for sufficiently dense objects, the escape velocity may be as fast as the speed of light -- or faster. Light rays from the surface of such an object would be unable to fly outwards to distant observers ... and, as a result, observers would see no light coming from the object; it would be black. We call such an object a black hole.
If we take the equation for escape velocity
[ 2 * G * M ]
escape velocity = sqrt [ ------------ ]
[ R ]
and turn it around to solve for the radius R of an object with a escape velocity c, the speed of light, we find
( 2 * G * M )
R = ( ------------ )
( c^2 )
If we plug in the Earth's mass, we find a radius of about 4 millimeters. In other words, if we could somehow squish the Earth until it was a ball about the size of a dime, it would turn into a black hole: no light would escape from its surface.
Q: What is the critical radius R for a stellar core with the Sun's mass?
The critical radius R at which the escape velocity is the speed of light is called the event horizon of a black hole. It isn't the "surface," but simply the point beyond which light cannot reach the outside. If you tossed a flashlight towards a black hole from a great distance, you could watch the flashlight fall towards the black hole, faster and faster and faster ... but when it reached the event horizon, its light would disappear.
Yes, yes, an observer watching this flashlight fall towards the black hole would actually see it fade, redden, and slow down as it gets very close to the event horizon. Your book talks about this in the section labelled "A Leap into a Black Hole." I just don't want to get into the general relativistic effects right now.
So, if we can't see them, how do we know that black holes exist?
There are two types of evidence for black holes, both somewhat indirect.
If a black hole sits in space all by itself, we don't see any light or radio waves or any electromagnetic radiation from it. It's invisible.

But if a black hole is surrounded by material -- from a nearby companion star, for example -- then an accretion disk may form around it ...
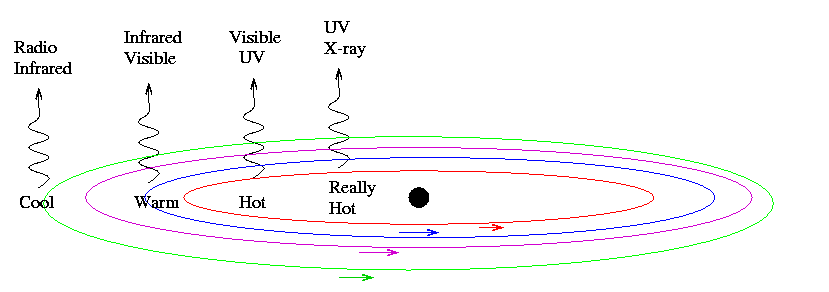
... and we may see radiation from the material in this disk. We can recognize these disks by several distinctive signatures:
For example, look at light emitted from the center of the galaxy called Markarian 421. There is a mixture of light of all wavelengths, due to material of different temperatures throughout an accretion disk:

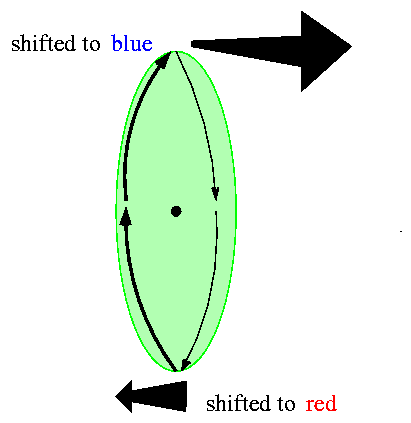
The Hubble Space Telescope acquired a spectrum of the center of another galaxy, M84, in visible light. Look at the shift in the wavelength of light from the two different sides of the center:
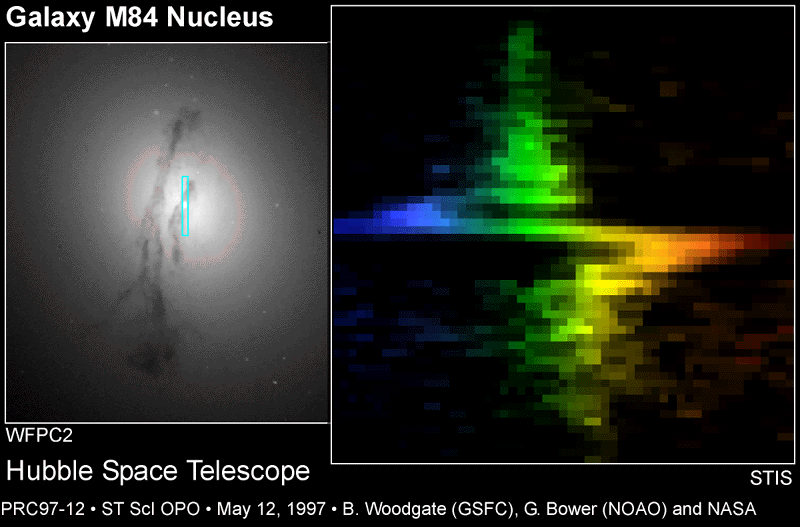
When we use the motions of the gas around these accretion disks at the center of galaxies to derive the mass of the objects at their centers, we find not 5 solar masses, or 10 solar masses, but MILLIONS of solar masses! Astronomers coined the term supermassive black holes to describe the objects at the centers of many galaxies -- very probably even our own Milky Way.
For reasons we don't yet understand, the accretion disks around some of these supermassive black holes appear to be shooting material outward in bipolar jets:

How do these gigantic black holes form? Why do they appear in the centers of so many galaxies? We just don't have the answers yet....
Astronomers have discovered many binary stars: systems in which two stars orbit around each other due to their mutual gravitational attraction. As Kepler and Newton showed centuries ago, if one can measure the period and the size of an orbit, one can determine the total mass of the system.
In the 1970s, astronomers focused their attention on an X-ray source called "Cygnus X-1" (which means "the brightest source of X-rays in the constellation Cygnus"). They eventually narrowed down the source of the X-rays to a star called HDE 226868. It was a big, hot, blue star -- but not hot enough to give off X-rays. Measurements of its spectrum showed that it was moving towards us and away from us in a periodic fashion:

In other words, it was part of a binary-star system, orbiting around a companion star. The visible star was much more massive than the Sun -- at least 9 solar masses, and probably double that. In order to whip it around in the observed way, its companion had to be pretty massive, too. However, despite its mass, the companion didn't seem to produce any visible light.
On the other hand, it did produce X-ray emission, which varied on short time scales. Could the companion be a rotating neutron star? No. A rotating neutron star would produce regular, periodic pulses of X-rays:
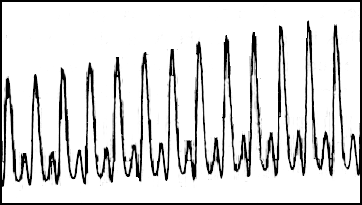
but Cygnus X-1 showed no periodicity in its X-ray emission:
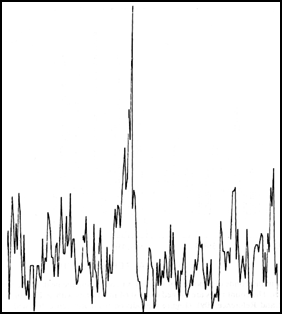
A black hole has no surface: material which falls into it doesn't slam into a rock-hard surface and create a blazing fireball of X-rays. Instead, it simply slides beyond the event horizon and disappears.
Measurements of the visible star's motion indicate that the mass of the companion object must be somewhere around 5 to 15 solar masses. The neutron degeneracy pressure which supports neutron stars against gravity breaks down at some point which isn't known precisely, but is something like 2 or 3 solar masses. The invisible companion to Cygnus X-1 is too massive to be a neutron star.
So, putting it all together, our current model of the Cygnus X-1 system looks like this:
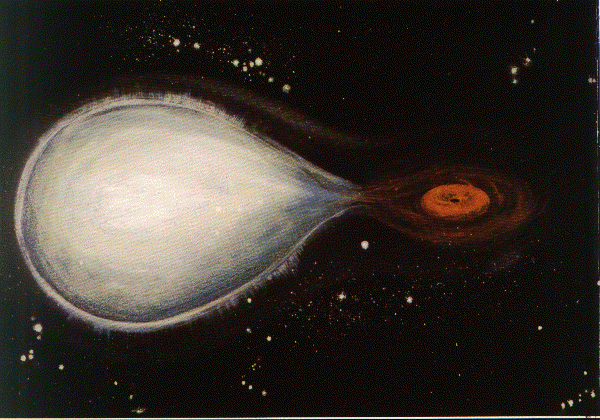
The massive star HDE 226868 and its tiny companion orbit around each other with a period of 5.6 days. Material from the hot star's outermost atmosphere is pulled into an accretion disk around the black hole. As it spirals inwards, the gas heats up and emits X-rays.
We now know of several other binary star systems in which accretion disks surround dark companions which are too massive to be neutron stars.
We can also detect the supermassive black holes at the centers of some galaxies by their gravitational pull on stars in those galaxies. For example, here's a picture of the central region of our own Milky Way:
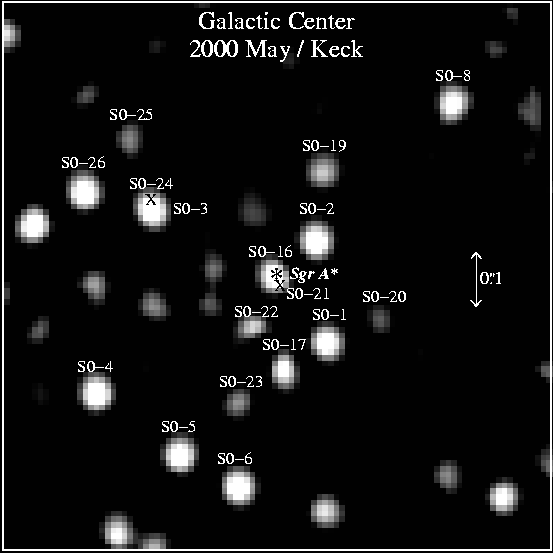
Image courtesy of
the UCLA Galactic Center Group
Q: Hey! How can you take pictures of the center
of the Milky Way? Isn't it obscured by dust?
A: Yes, dust blocks the visible light ... but not
the infrared light. So use an infrared telescope.
If we take pictures year after year after year, we can actually SEE stars moving as they orbit something massive at the center of the galaxy:
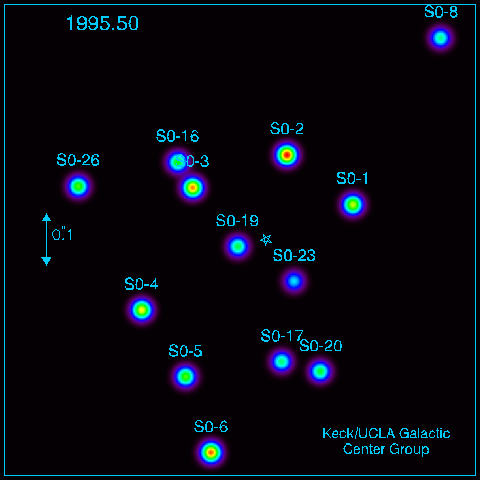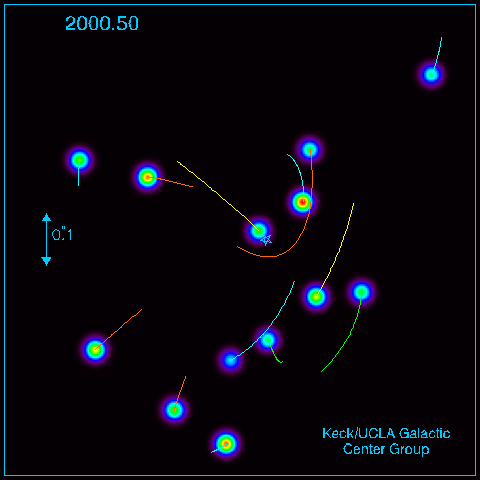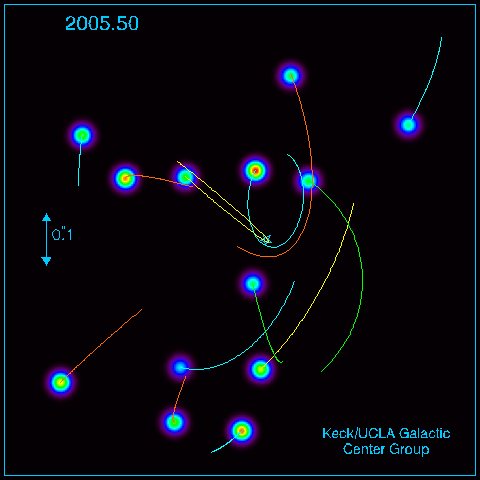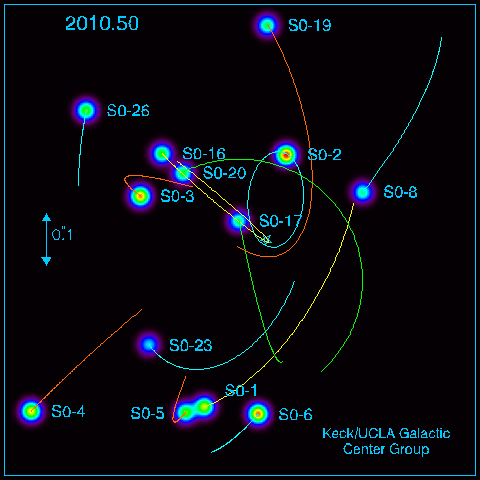
Image again courtesy of
the UCLA Galactic Center Group
Using the measured motions and Newton's Law of Universal Gravitation tells us that the central mass must be several million solar masses ... which, very likely, is a black hole.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.