 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Recall that astronomers have noticed a curious set of properties shared by Active Galactic Nuclei and quasars:
Is there any way to explain these features with a single model? Yes -- over the past few decades, astronomers have settled on The Unified Model for AGN. The key feature is a supermassive black hole at the center of a galaxy.
How does a black hole (BH) explain all the above features? At first thought, it would seem to be the worst possible explanation, because a BH sucks material (even light!) into its event horizon. So how could it cause the emission of huge amounts of light, radio and X-rays? The answer is -- it doesn't, itself. Instead, before the material reaches the BH, it forms an accretion disk around it -- and the accretion disk is responsible for most of the observed properties of AGN and quasars..
Let's focus on the accretion disk, and ask four questions:
Okay, maybe that was too short. The idea is this: material in a galaxy orbits around the center. In most galaxies, especially those with signficant amounts of gas and dust, most of the material orbits in the same direction -- say, counter-clockwise around the center. Matter which moves around a central point has a property called angular momentum, which can be calculated as
ang mom = (mass) * (distance from center) * (speed)
If an object's orbit is somehow perturbed so that it
passes close to the BH, it still maintains its angular
momentum as it draws near: angular momentum is conserved,
just as linear momentum is.
As it gets closer to the BH, its speed around the BH
increases -- and it keeps orbiting in the same direction.
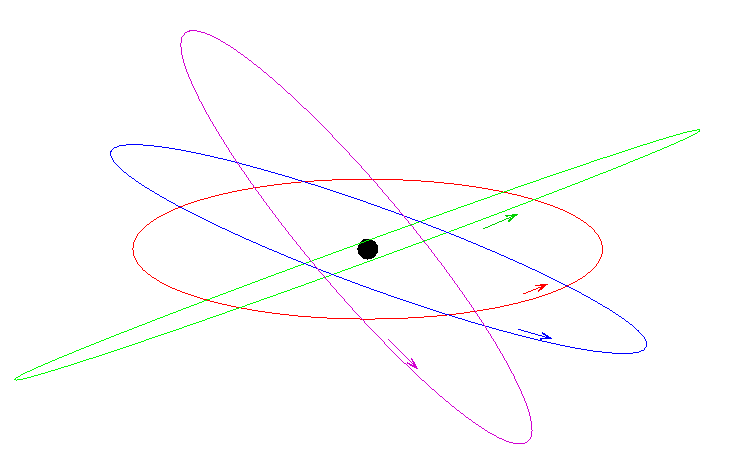
Consider a bunch of little gas clouds which were all originally in orbits counter-clockwise around the center of a galaxy. If they all are perturbed so that their orbits pass close to the center of the galaxy, they might at first end up with orbits tilted at different planes:

As these gas clouds revolve around the BH on their tilted orbits, they occasionally collide with each other. Now, because both clouds are going around the BH in the same direction (counter-clockwise), the collision doesn't change this component of their motion. But the collision DOES change the vertical component of their motion: it tends to decrease the vertical speed of each, bringing them closer to the average vertical speed -- which is zero. After many collisions, the clouds lose all their vertical motion, but retain their counter-clockwise motion. The result is a thin disk of rotating gas:
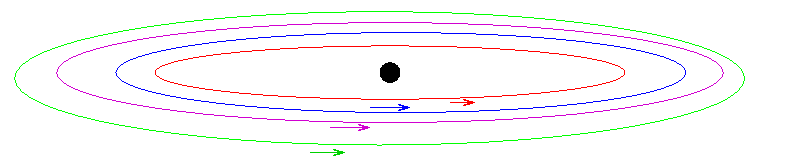
Disks like this are found in many astronomical contexts: for example, the rings around the planet Saturn:

and the gas and dust clouds orbiting around a spiral galaxy:

Recent observations hint at the accretion disks at the center of galaxies (though we still can't resolve the actual disks with optical telescopes):
"Friction?" you might say. "What does that mean?" We ordinarily think of friction as a consequence of two solid surfaces rubbing together. But a similar effect occurs when two streams of gas move past each other at different speeds: collisions between the particles cause them to speed up, which in turn means that the temperature of the gas increases.
Recall that when material moves in a circular orbit around a massive central object, its orbital speed is given by
[ G * M ]
V = sqrt[ ----- ]
[ R ]
where
G = 6.67 x 10^(-11) N*m^2/kg^2
M is the mass of the central object, in kg
R is the radius of the orbit, in m
Ordinary black holes have a mass roughly equal to that of the sun: about 10^30 kg. Astronomers believe that the black holes at the centers of AGN are "supermassive:" they have masses a million times larger, or more. Consider a supermassive black hole with mass M = 2 x 10^36 kg, about one million solar masses, and radius R = 3 x 10^9 m, which is about 5 times the radius of the sun. Material orbiting around this BH would have speeds like this:
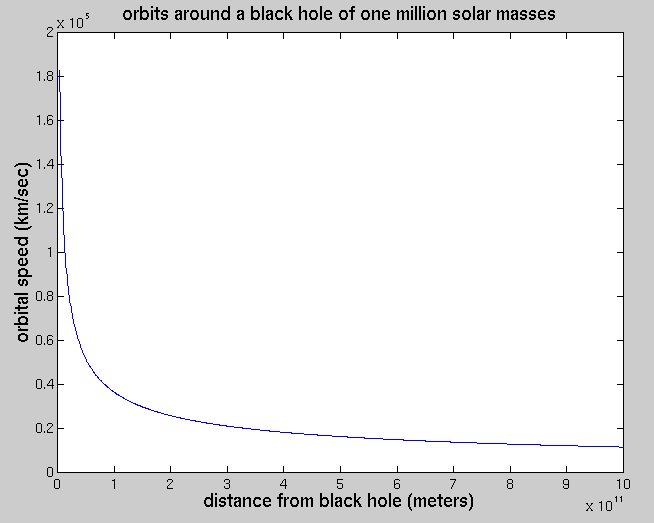
Note how fast it's moving: an object as far from the BH as the Earth is from the Sun, 1.5 x 10^(11) meters, would be orbiting at about 30,000 km/sec -- which is about 1,000 times faster than the Earth moves around the Sun.
Now, material at one orbital radius R will be moving slightly slower than material a bit closer to the BH, at R - a bit, and slightly faster than material a bit farther from the BH, at R + a bit. This means that it will be passed by the material closer to the BH -- which might cause some collisions as it goes past -- and it will itself move past the material a bit farther from the BH -- again, possibly colliding with its particles. In addition, any turbulence stirred up by these collisions will greatly increase future collisions.
The bottom line is that some of the kinetic energy of the orbiting gas is transferred into thermal energy of atoms and ions within the gas. That's the key.
As material comes closer and closer to the BH, its orbital speed increases ... which means that collisions between material at slightly different radii become more violent. That means that the temperature of the material increases. For a typical supermassive BH at the center of a galaxy, it can be shown that the temperature of the gas at a distance r from the BH is
6 R 0.75
T = 4 x 10 [-----] Kelvin
r
where R is the radius of the BH.
In tabular form,
distance from BH distance Temperature
in units of R in meters (K)
-------------------------------------------------------------------
2 R 6 x 10^9 2,300,000
3 R 1 x 10^10 1,700,000
30 R 1 x 10^11 300,000 Earth's dist from Sun
300 R 1 x 10^12 53,000 Saturn's dist from Sun
3000 R 1 x 10^13 9,500 twice Pluto's dist
30,000 R 1 x 10^14 1,700
300,000 R 1 x 10^15 300 200 times Pluto's dist
-------------------------------------------------------------------------------
So, the disk is really big -- much larger than our solar system. It's full of hot, warm, and cool gas. The gas radiates at a very wide range of wavelengths, producing a broad mix of radiation.
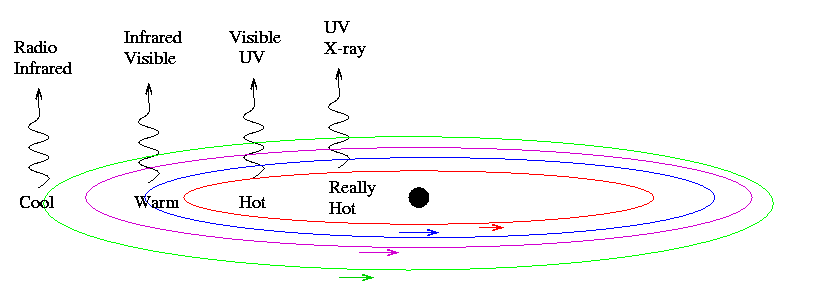
And this radiation from the disk causes the very bright nuclei in AGN and quasars; but note that even the hottest gas, very close to the BH, is too cool to produce gamma-rays. Hmmmm.....
It turns out that the amount of energy produced by an accretion disk depends in part on the amount of gas falling onto it: more infalling gas means much brighter radiation, at all wavelengths. Most of the gas in galaxies moves in circular orbits in a stable disk -- far, far from the center. But if a nearby companion galaxy flies past, its gravitational pull may knock some of the gas out of its circular orbit and into orbits which pass closer to the galaxy's center. This might explain why many active galaxies have close neighbors: the gravitational pull of those neighbors has caused lots of gas to fall in towards the center, feeding the monster.
What causes material to shoot outwards from the vicinity of a black hole? I don't know, and I don't think that any astronomer really knows. There are a number of models which explain some of the story, but as far as I know, none explain everything. Most involve very complicated interactions between the magnetic field of the BH and the charged particles making up the accretion disk. The simple picture is something like this:
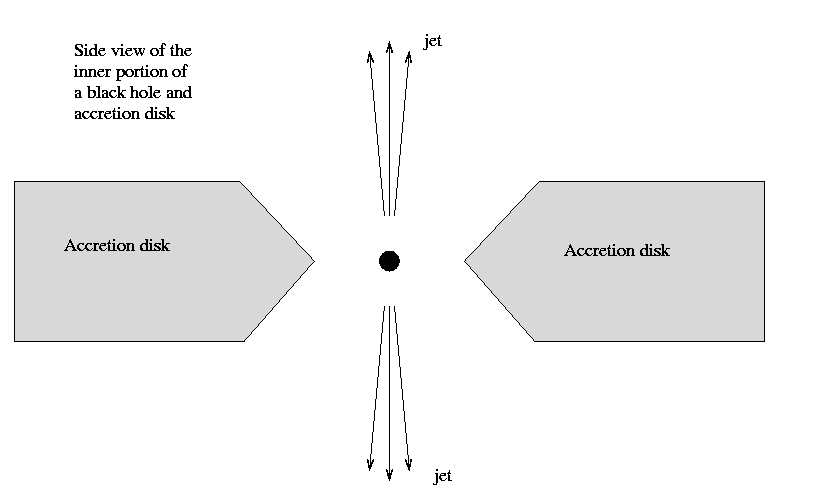
The accretion disk pinches down at its closest approach to the black hole. This creates open space directly above and below the BH, perpendicular to the plane of the accretion disk. Something accelerates a small fraction of the infalling particles to very high speeds and shoots them into this open space, forming jets in opposite directions. By "very high speeds", we mean relativistic speeds, extremely close to the speed of light:
particle speed >= 99% speed of light
The relativistic particles remain in a coherent jet for a long, long time as they shoot outwards, probably due to their interaction with a strong magnetic field. As they move through the magnetic field, they emit synchrotron radiation at radio, IR, visible, and X-ray wavelengths. We can see this radiation directly if we look closely at the jets.
As the relativistic particles in the jets fly outwards, they may collide with photons emitted by the hot material in the accretion disk.
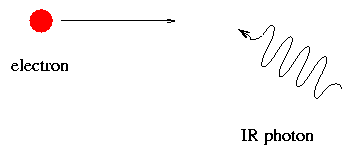
radio photons ---> optical photons
optical photons ---> X-ray photons
X-ray photons ---> gamma-ray photons
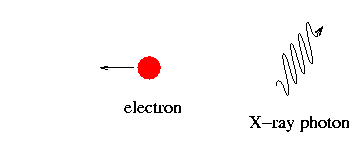
It is these collisions which produce the gamma rays we observe from some AGN and quasars.
When the relativistic particles in the jet smash into any surrounding material, they push it out of the way. Over a period of millions of years, they can carve out big bubbles or lobes in the surrounding medium. The low-density gas inside these lobes emits more synchrotron radiation as it gradually slows down.
The primary piece of evidence comes from spectroscopy: breaking light into its different wavelengths. If we look at the spectrum of an ordinary star, we see absorption lines due to cool gas above the star's visible surface.

The lines are very narrow, because the gases in a star move slowly. In a star like our Sun, the difference between the velocity of gas on one side (coming towards us) and the other side (moving away from us) is only about V = 3 km/sec. The Doppler shift in the wavelength of light radiated by (non-relativistic) moving objects is
v
(change in wavelength) = (rest wavelength) * (---)
c
as long as the speeds are small compared to the speed of light.
If we look in the middle of the visible range, at
a wavelength of 5000 Angstroms,
we find for the Sun
v = 3 km/sec
3 km/sec
change in wavelength = 5000 * (--------------)
300,000 km/sec
= 0.05 Angstroms
So the lines are narrow.
If we look at a typical spiral galaxy, we see light from many stars all at once. All of the stars have these dark absorption lines ... but due to the stellar motions, they are shifted by different amounts. This yields broad dark lines in the galaxy's spectrum, with a width
v = 300 km/sec
300 km/sec
change in wavelength = 5000 * (--------------)
300,000 km/sec
= 5 Angstroms
The lines of such a galaxy are relatively broad:

Now, if light is emitted by material in an accretion disk, it comes from material with much higher velocities. In an accretion disk around a BH of one million solar masses, gas at a distance of about 10^13 meters (about 100 AU) has a temperature of 10,000 Kelvin -- just right for producing visible radiation. This material is moving at high speeds:
v = 3600 km/sec
3600 km/sec
change in wavelength = 5000 * (--------------)
300,000 km/sec
= 60 Angstroms
So, in this case, we might expect to see very broad lines which are bright -- because this gas is emitting radiation, not absorbing it. And, in fact, when we take spectra of AGN and quasars, that's exactly what we find:
But wait -- there's even more direct evidence for accretion disks. A few galaxies are so nearby that we can resolve the two sides of the accretion disk:
And in a few cases, we can actually see this:
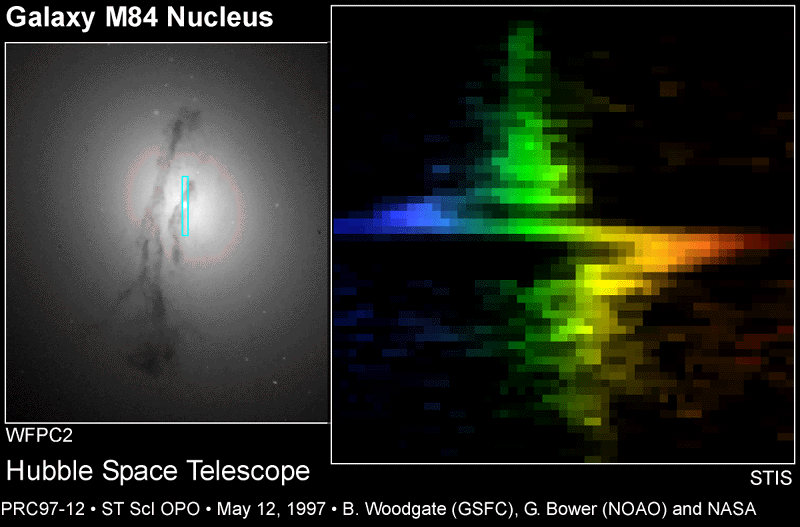
Finally, there are a very few galaxies which have special little clouds of gas in their accretion disk: water molecules in these clouds emit strong radio waves of a particular known wavelength. When we use radio interferometers to examine these galaxies, we can distinguish each little cloud of gas, and measure both its position and velocity very accurately. Not only do we see that material on one side is moving towards us, and material on the other away from us:
But we can actually compare the measured distance of each cloud from the center, and its observed velocity, to the prediction of the standard accretion disk model, in which
[ G * M ]
V = sqrt[ ----- ]
[ R ]
And, mirabile dictu, the actual gas clouds fit
the model exactly.
Additional resources:
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.