Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
When we look up into the sky at night, we see some stars which appear very bright, and others which are so faint that we can barely detect them.
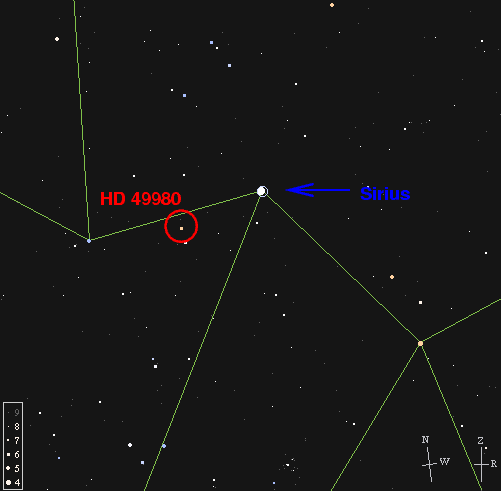
The star Sirius, for example, has a magnitude of about -1.5; a bit more than one degree away, the star HD 49980 shines relatively feebly at magnitude 5.8.
Q: How many times brighter does Sirius appear?
Q: Does this mean that Sirius is a much more powerful star,
one which emits hundreds of times as much energy
as HD 49980?
No!
The reason, of course, is that two factors determine the apparent brightness of a star in our sky.
In this particular instance, the apparent magnitude of these two stars, based on their apparent brightness is quite misleading.
apparent magnitude: a measure of the brightness a star appears to have as we observe it in the night sky from Earth
It turns out that Sirius is one of the closest stars to the Sun; it is only 2.64 parsecs away. A parsec is a unit of distance equal to about 3.3 light years, or 3.1 x 1016 meters; we'll discuss this unit later. On the other hand, HD 49980 is very distant, located about 500 parsecs from the Sun.
Q: How many times more distant is HD 49980?
Q: If we were to pick up Sirius and move it
so that it was at the same distance as HD 49980,
how many times fainter would it become?
Q: Which star would look brighter if they
were sitting side-by-side at the same distance?
Since we often want to compare the intrinsic properties of stars, we'd like to have some measure of brightness which is connected directly with luminosity; a type of magnitude which does not depend on distance. Astronomer convert apparent to absolute magnitudes to compare stars fairly, as if they were all side-by-side at a standard distance.
absolute magnitude: the magnitude a star would have, if it were moved to a distance of 10 parsecs from the Sun.
The ordinary convention is to write apparent magnitudes with a lower-case letter m, and absolute magnitudes with an upper-case M. One can derive a formula which connects the apparent and absolute magnitudes of a star, using the inverse square law. If we express the distance d in parsecs, then
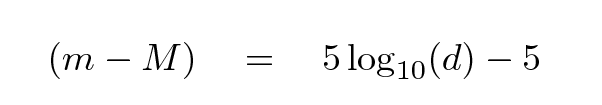
Q: The distance to Sirius is 2.64 pc, and its apparent
magnitude is m = -1.5. What is the absolute magnitude
of Sirius?
Q: The distance to HD 49980 is 500 pc, and its apparent
magnitude is m = 5.8. What is the absolute magnitude
of HD 49980?
Stars with small absolute magnitudes are truly luminous beasts, radiating huge amounts of energy into space each second. Stars with large absolute magnitudes are relatively feeble creatures, dimly illuminating their immediate surroundings but little else.
As some of you have already noticed, the magnitude scales -- both apparent and absolute -- are defined in relative terms: this star is 10 times brighter than that one. Is it possible to attach real physical units to the intensity of light coming from a star if we know its magnitude? In other words, can we measure the zeropoint of the magnitude scale?
To a first approximation, yes, we can. The precise flux of energy from a star depends on a number of factors
1,000,000 photons
A star of apparent magnitude 0 has a flux ------------------
second * sq.cm.
In other words, each second, one million photons from the star would enter a box of area one square centimeter.
Q: You look at Vega, a star of apparent magnitude m=0,
with a telescope of diameter d = 6 inches = 15 cm.
How many photons enter the telescope each second?
If you prefer to express the flux in terms of energy,
3 x 10^(-13) Joules
A star of apparent magnitude 0 has flux = ---------------------
second * sq.cm.
= 3 x 10^(-9) Watts / sq.meter
We can also figure out a very rough value for the absolute magnitude scale. Again, there are a lot of complications in defining the precise value, but to an order of magnitude
28
A star of absolute magnitude 0 has power 3 x 10 Watts
Q: The Sun has an absolute magnitude of about M = 4.8.
What is the power of the Sun?
The difference between the apparent and absolute magnitude of a star, (m - M), is called its distance modulus.
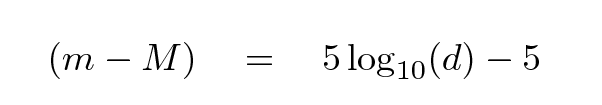
As the equation above shows, it is a simple function of the distance to the star. In practice, astronomers sometimes prefer to specify the distance to a star by its distance modulus, rather than by the distance itself. For example, Look at an extract from the abstract to this paper on the distance to stars in the galaxy NGC 2403:
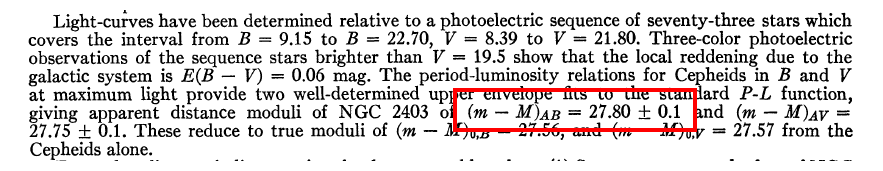
Why use distance modulus instead of distance? I can think of two reasons, though they really boil down to the same thing.
Q: Joe Astro is studying the Andromeda galaxy.
He notices a star in that galaxy which appears
similar in many ways (color, temperature, etc.)
to the Sun. The apparent magnitude of this
solar twin is m = 30.0.
What is the distance modulus to the Andromeda
Galaxy?
The basic idea is that, from a practical, observational point of view, it is often more useful to have a catalog of distance modulus values instead of real distances.
A second advantage appears when astronomers use distance modulus as a relative measure between two objects. For example, the Large Magellanic Cloud (LMC), the nearest galaxy to our own Milky Way, is often used as a stepping-stone to other, more distant galaxies. Our current estimate of the distance to the LMC is about 50,000 pc = 50 kilo-parsecs (kpc). Suppose that you measure the distances to the LMC and several other galaxies by observing a particular sort of star in each galaxy. You might find
apparent mag distance modulus distance
galaxy of star relative to LMC (kpc)
------------------------------------------------------
LMC 16.5 0.0 50
M31 24.3 7.8 1800
M81 26.8 10.3 5740
------------------------------------------------------
Ten years from now, astronomers discover a systematic error in measurements to the LMC; instead of being 50 kpc away from us, it actually turns out to be 60 kpc away.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.