 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
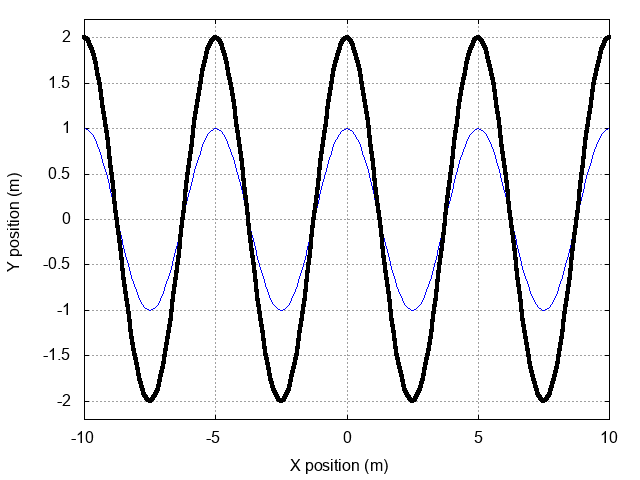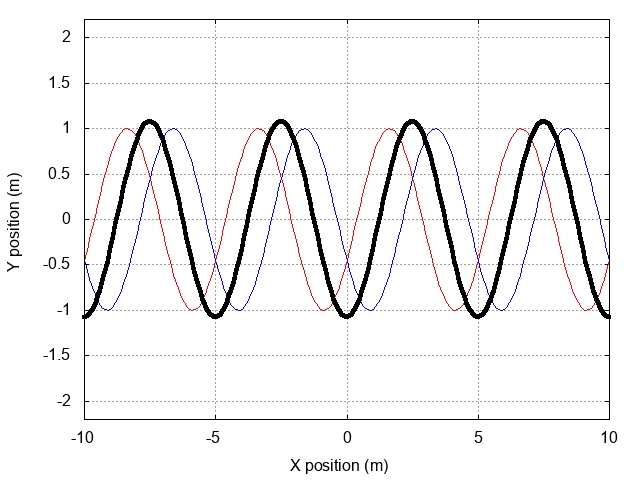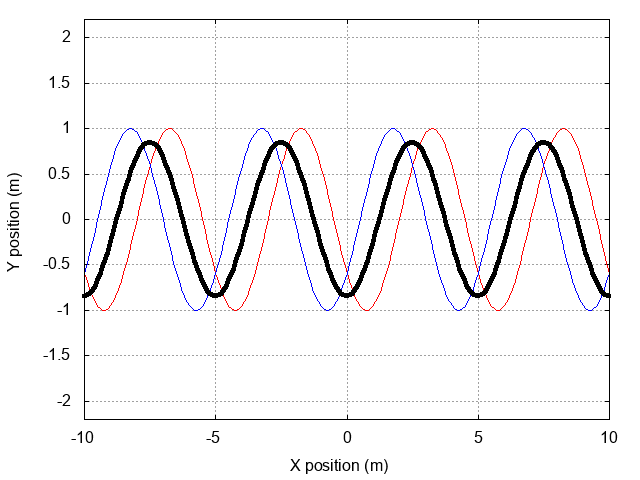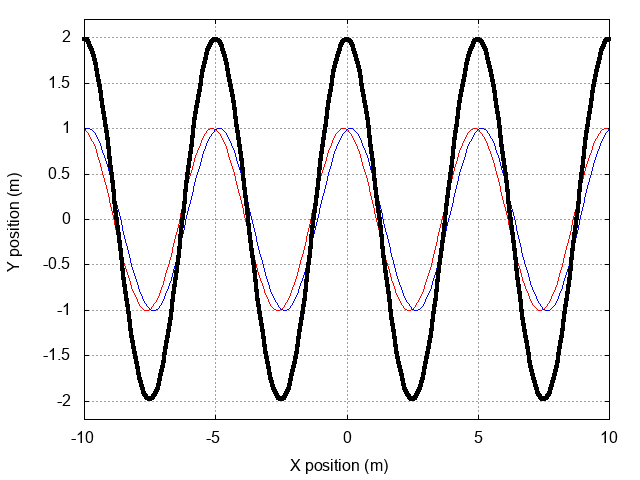
We've used this very important idea several times already, so it's probably a good idea to state it clearly. SUPERPOSITION means that when two waves meet, the result is simply the sum of the individual waves.
This explains how two identical waves, travelling in opposite directions, can create a standing wave where they meet.

In mathematical terms, we can simply add
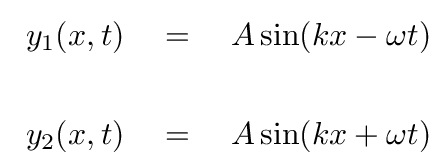
to find the equation of the combined wave
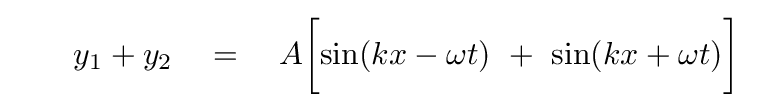
Now, as we saw earlier, we can gain insight on this combination by applying a trig identity:
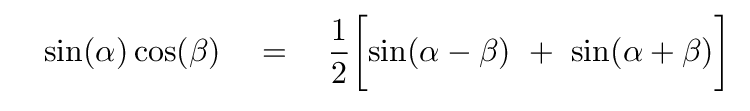
That identity can turn our expression for the sum of the two waves into the form
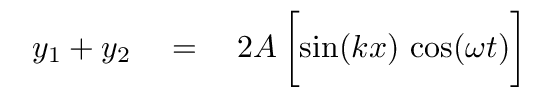
This is clearly a stationary, or standing, wave, as the functions of space and time are separated. We see a fixed shape, the amplitude ONLY of which changes over time.
Right.
Let's now apply this principle of superposition to a slightly different situation. The results will be familiar, at first, but we will then extend the application to new territory, and learn something about the speed with which groups of waves move.
What happens if two travelling waves with slightly different frequencies should meet? Our starting point will again be two waves, but this time, they don't have the same frequency or wave number; but they are moving in the same direction.
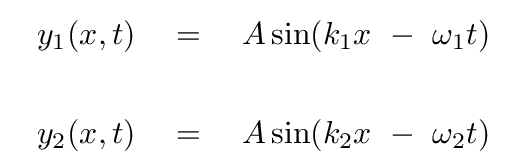
If the two frequencies are NEARLY the same, then we can write
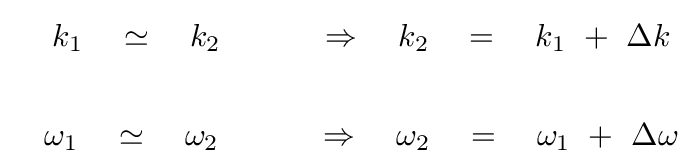
If these waves are moving through a non-dispersive medium, then they will have the same speed.
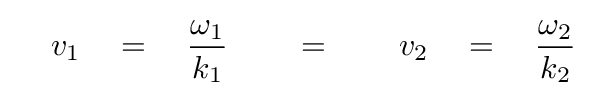
What happens when we add together these two waves?
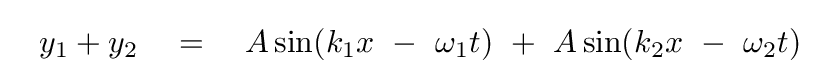
Hmmm. We can't use the previous trigonometric identity to add these two waves, because the terms in the arguments are different. Fortunately, a different identity leaps to our rescue:
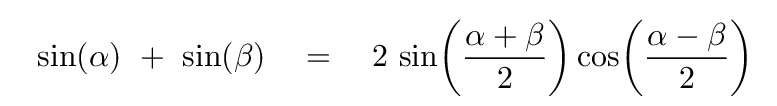
So, if we define
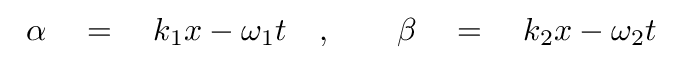
then we can calculate the sum of the two waves in the following manner:
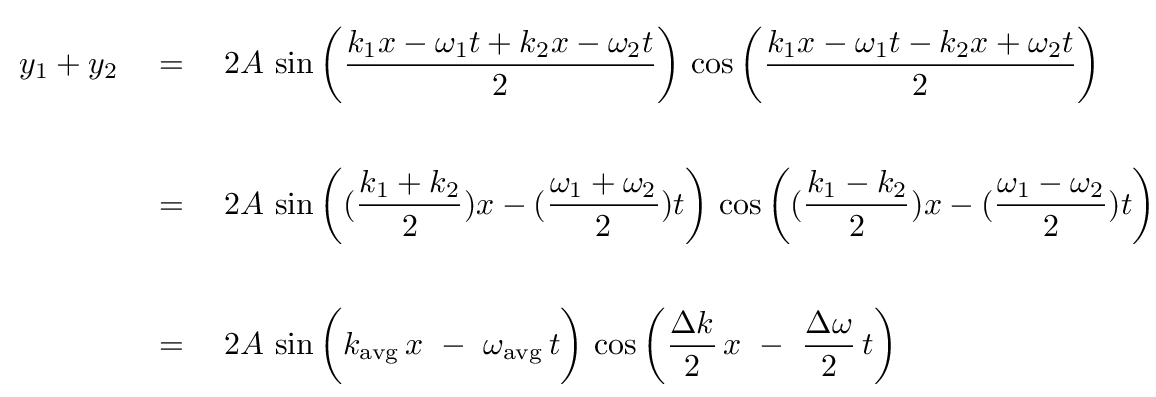
You might recognize this product of two waves as the source of a pattern of BEATS.
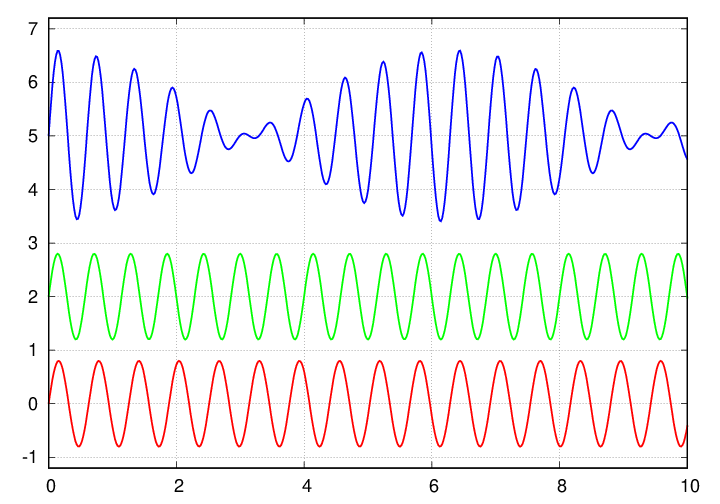
Let's go through some numbers for an example pair of waves:
wave 1 wave 2
------------------------------------------------------------------------------
wavelength lambda 500 nm 505 nm
7 7
wavenumber k 1.256637062 x 10 rad/m 1.244195110 x 10 rad/m
15 15
angular freq omega 3.767303135 x 10 rad/s 3.730003104 x 10 rad/s
combined wave
"average" wavelength
"envelope" wavelength
------------------------------------------------------------------------------
Note how much larger the wavelength of the envelope is, compared to the wavelength of the "average" wave.
In a vacuum, the two waves will create a beat-like pattern which progresses steadily with the same speed as its two constituent waves. But if the waves enter a region filled with a dispersive medium, the individual waves no longer have the same speed. What happens to the combined wave then?
For example, suppose our two sample optical waves enter a piece of crown glass. The refractive index of this material is greater than 1, so the waves slow down; but because the index changes slightly with wavelength, the waves slow down by slightly different amounts.
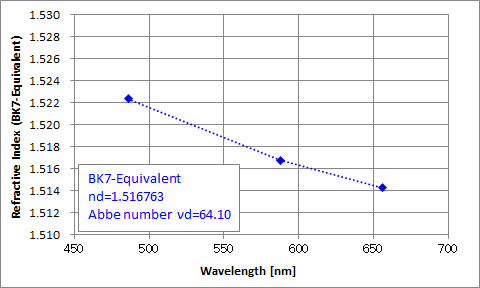
Using on the graph above, I measured indices of refraction. Can you fill in the table? I've already filled in the "angular frequency in glass" column, because it is exactly the SAME as in a vacuum. When light waves move from one medium to another,
wavelength index wavelength wavenumber ang frequency speed
in vacuum of refr. in glass in glass in glass in glass
(nm) (nm) (rad/m) (rad/s) (m/s)
-------------------------------------------------------------------------------
15
500 1.5214 3.7673 x 10
15
505 1.5211 3.7300 x 10
-------------------------------------------------------------------------------
The key here is that in a dispersive medium, waves of different frequency travel at different speeds.
So what would happen if we created simultaneously a pair of waves with these properties, then allowed them to enter a piece of glass?
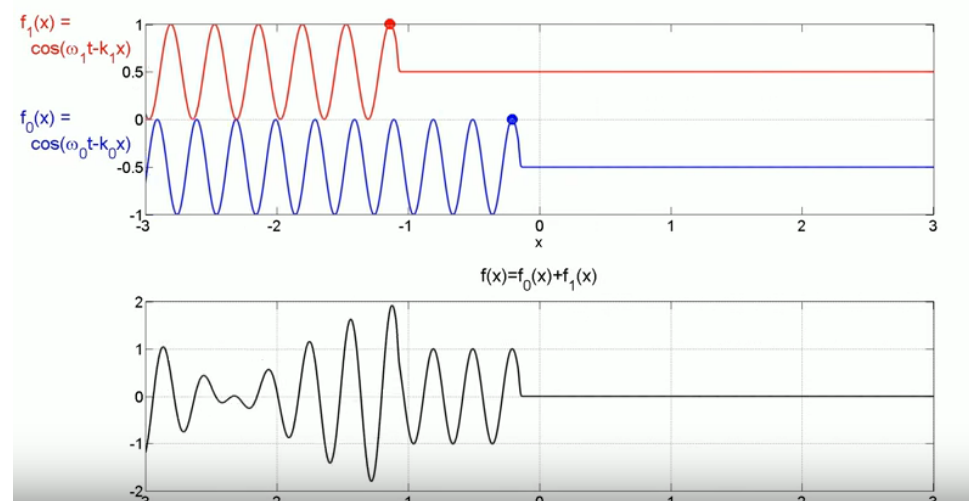
Image taken from the video
Group Velocity / Phase Velocity Animation - Case 1: Group Velocity larger than Phase Velocity .
Thanks very much to meyavuz!
This variation in shape complicates the measurement of the combined wave. Physicists have settled on two different ways to measure "the speed" of this sort of travelling wave:
Let's look at each one.
Phase velocity, abbreviated vp, is based on the motion of one particular "phase" in the average wave. In the video below, pay attention to the green dot that appears about 30 seconds in.
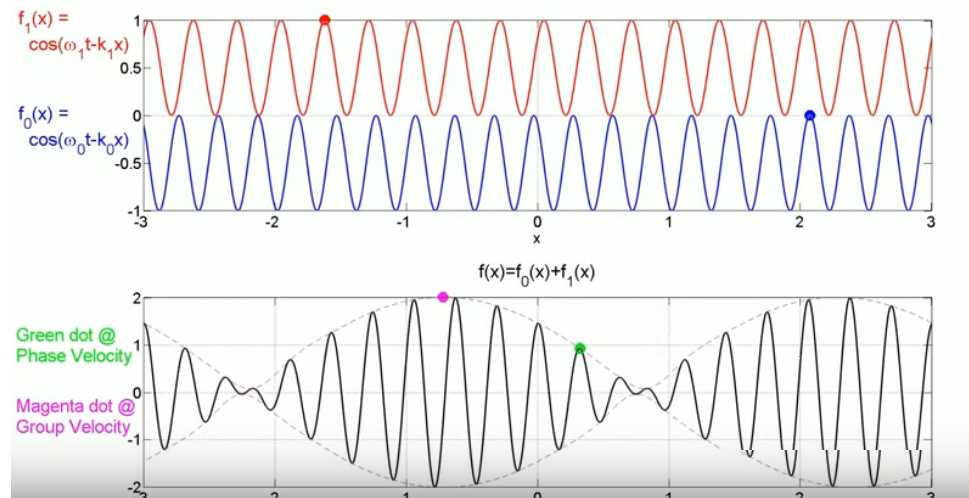
Image taken from the video
Group Velocity / Phase Velocity Animation - Case 1: Group Velocity larger than Phase Velocity .
Thanks very much to meyavuz!
Recall that the combined travelling wave has an equation
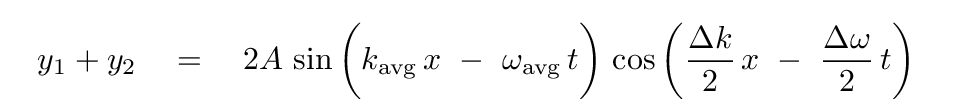
The phase velocity can be calculated as
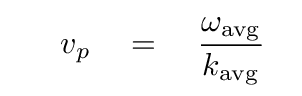
It is clearly very similar to the velocity of either of the individual waves.
On the other hand, the group velocity, abbreviated vg, is based on the motion of the "envelope" of the combined wave. In the video below, pay attention to the magenta dot that appears about 30 seconds in.

Image taken from the video
Group Velocity / Phase Velocity Animation - Case 1: Group Velocity larger than Phase Velocity .
Thanks very much to meyavuz!
Since the group velocity is based on the second, "envelope" term,
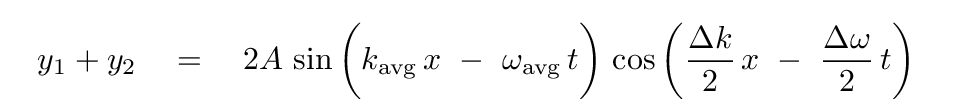
we can compute its value like so:
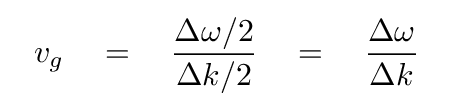
If we pick two waves with VERY similar frequencies and wave numbers, then the group velocity approaches
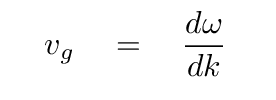
Depending on the properties of the medium, this may be close to the phase speed, or very different.
The first animation featured a group velocity which was larger than the phase velocity. But there are, mathematically speaking, other possibilities.
For example, the phase velocity may be larger than the group velocity.

Image taken from the video
Group Velocity / Phase Velocity Animation - Case 5: Positive Phase and Negative Group Velocity .
Thanks very much to meyavuz!
Here's a case where the group velocity of a combined wave is ZERO!

Image taken from the video
Group Velocity / Phase Velocity Animation - Case 2: Zero Group Velocity .
Thanks very much to meyavuz!
Let's go back to our example of two light waves passing through a piece of crown glass. In the table below, for the "envelope" column,
Please compute the two velocities for this combined wave: the phase velocity, in the left column, and the group velocity, in the right column.
"average" wave "envelope" wave
-------------------------------------------------------------------
15 13
angular freq 3.74865 x 10 1.86500 x 10
(rad/s)
7 4
wavenumber 1.90219 x 10 9.65122 x 10
(rad/m)
velocity vp = vg =
(m/s)
-------------------------------------------------------------------
So, when waves of two (or more) frequencies combine and travel as a group, we have a choice of two velocities. Which one should we use to describe the combination?
In the majority of cases, the group velocity is the important one. Why?
Since we are usually interested in the interaction of a set of waves with some atoms, or instruments, and since those interactions involve the exchange of energy, it makes sense that the group velocity is the one that we should associate with the "speed of the combined wave."
Consider an electromagnetic wave travelling through a vacuum, with angular frequency ω, wavelength λ, and wave number k = 2π / λ. In a vacuum, the wave clearly moves with velocity c = ω/k.
Now, if that wave passes into a medium with refractive index n, then some of its properties may change -- but others may stay the same. In particular,
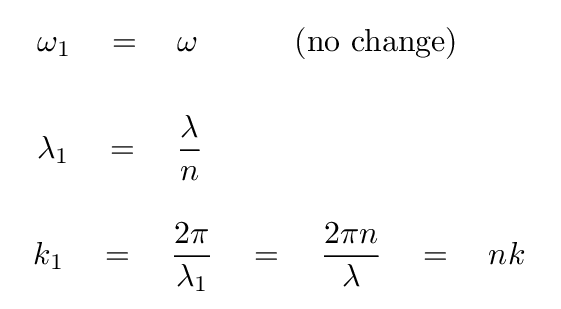
That means that the phase velocity in the medium will become
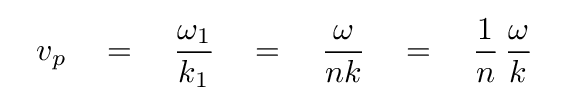
Since this is an electromagnetic wave,
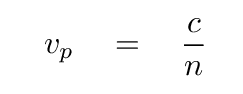
Simple enough.
The group velocity is a bit more complicated. We can with a bit of work derive a relationship between the phase velocity and group velocity. Start with the general definition of the phase velocity

We can thus write the angular frequency of an electromagnetic wave as a function of its wave number and the index of refraction.
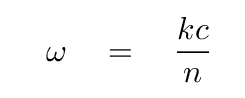
Now, one definition of the group velocity is the derivative with respect to wave number.
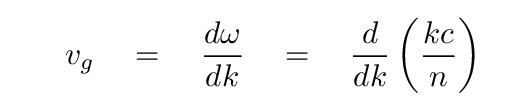
What is the result?
Q: What is this derivative?
You might think that the derivative is simply c/n, but that assumes that neither c nor n might depend on the wave number k. Of course, the speed of light in a vacuum, c, really is a constant, so we don't have to worry about that ... but since the index of refraction MAY change with wavelength (as we have seen), then it may change with wave number, too. That means that this derivative must take into account the possible change of index with wave number.
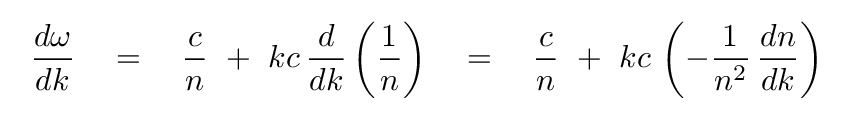
And so the total derivative of angular frequency with respect to wave number becomes
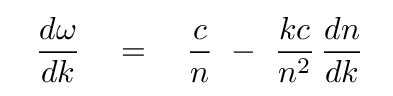
This derivative is the very definition of the group velocity, so we can write

Aha! The first term on the right, c/n, is just the phase velocity. So, in the end, the group velocity can be expressed as the phase velocity multipled by a certain factor.


Look at the graph above, which shows the index of refraction n as a function of wavelength λ. The slope is the change in n as a function of λ; in other words, the slope is dn/dλ.
1) Is dn/dλ positive or negative for this material?
2) Is dn/dk positive or negative for this material?
3) Is the group velocity faster or slower than the phase velocity
in this material?
For most ordinary materials, the derivative dn/dλ is negative. Remember this graph? Just look at the slope: negative!

Since the wave number k is proportional to the reciprocal of wavelength, it falls when λ rises, and vice versa; therefore, if dn/dλ is negative for ordinary materials, the derivative dn/dk must be positive for ordinary materials.
For most substances, therefore, the group velocity is smaller than the phase velocity.
In some unusual circumstances or special materials, it may be possible that

In such cases, it is mathematically possible that the group velocity may be larger than the phase velocity. In some cases, it may even be true that the group velocity is greater than c ... BUT careful consideration of the physical nature of these situations has shown that, no, neither information nor energy can travel faster than c.
See the final two references in the section below for more information.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.