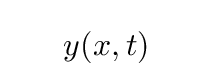
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
In an earlier lecture, we analyzed the forces on a 1-dimensional string with linear mass density μ, placed under tension T, and stretching in the x-direction. If at some location x, the string were displaced from equilibrium in the y-direction, and then released, a disturbance would move away from x along the string such that the vertical position of the string
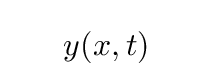
would satisfy the equation
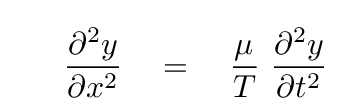
That combination of mass density and tension turns out to be related to the speed of the propagation of the disturbance along the string,
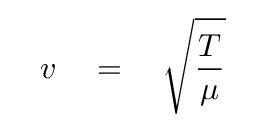
which allows us to write the relationship (aka "the wave equation") in the following manner.
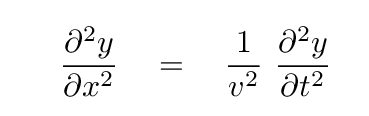
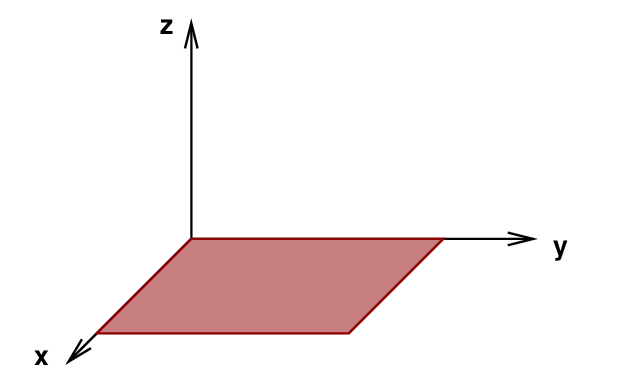
Let's move to a medium which is two-dimensional: a flat plane defined by the x and y axes. Suppose we stretch a sheet of rubbery material between these axes.
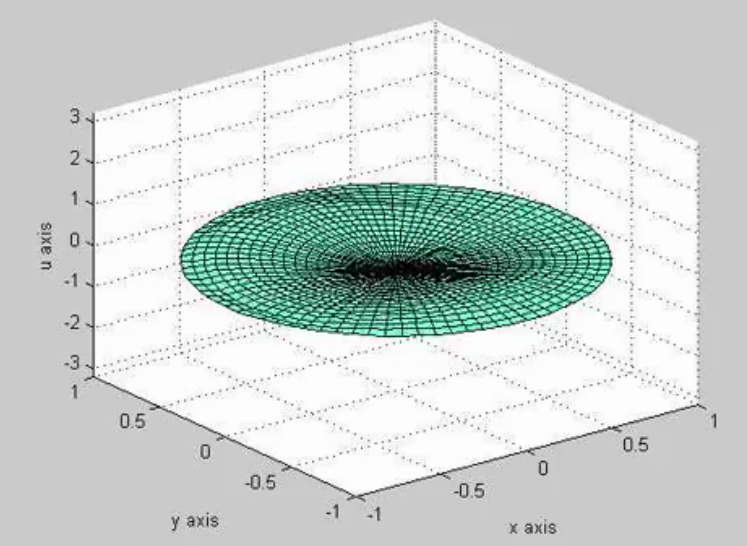
If we pull some piece of this sheet vertically up or down, and then release it, disturbances in the z direction may flow outward in both the x and y directions. (Click on image below to watch a movie)
Video courtesy of
Waves in a Circular Membrane
posted by
Kenneth Gollins
In this case, we must describe vertical motions of the membrane as a function of the (x, y) position of each point on the sheet, as well as a function of time.
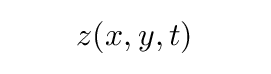
We can follow a line of reasoning very much like "forces on a tiny section of string" to derive a differential equation which governs the motion of these disturbances.
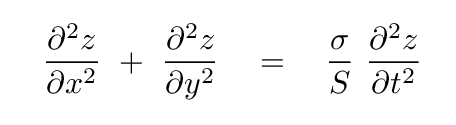
Here,
Q: Is there any physical significance to the factor σ/S
on the right-hand side of this equation?
Yes, of course. That ratio is related to the speed with which disturbances will move across the membrane.
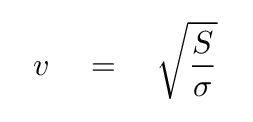
Suppose we create a flat rectangular plate, of length Lx and width Ly, and clamp the plate around the edges.
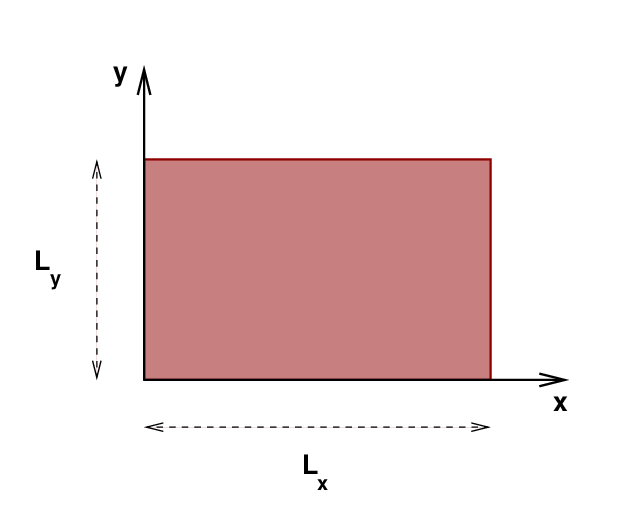
Since the edges of the plate are held fixed, the vertical position of the edges must be exactly zero at all times. This provides the boundary conditions we will need in order to solve for the normal modes of oscillation on the plate.
We begin by making a guess: the vertical position of the plate may be written in a separable manner, as the products of separate functions of the three variables x, y and t.
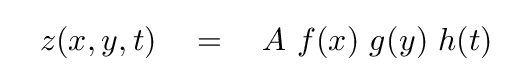
If we choose one particular value of y, and look at the little thin strip of the plate at this fixed y-position, we see that the vertical displacement must be zero at the left end (x = 0), and also zero at the right end (x = Lx). That looks somewhat like a string of length Lx, doesn't it?
Based on our experience with the normal modes of motion along a string, we might guess that the vertical height along this strip might be
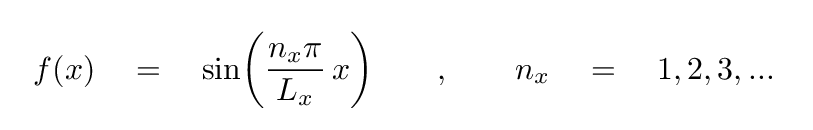
In a similar manner, if we consider one particular value of x, and look at the strip of plate which runs from y = 0 to y = Ly, we might guess

Again drawing on our experience with the behavior of 1-D strings, we can guess that the time dependence might be expressed as a simple sine or cosine. Let's pick a cosine function -- we can always add some phase offset if necessary to satisfy additional initial conditions.
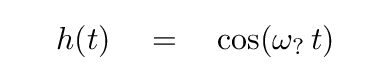
But ... hmmm. What should we use as the frequency of this motion?
Does the frequency of oscillation depend on
a) the index of variation in the x-direction nx
b) the index of variation in the y-direction ny
c) both
d) neither
It should depend on both of those indices, so we can write
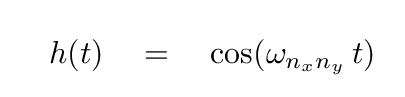
Right. Putting all the pieces together, our GUESS is that the displacement of the plate can be written as
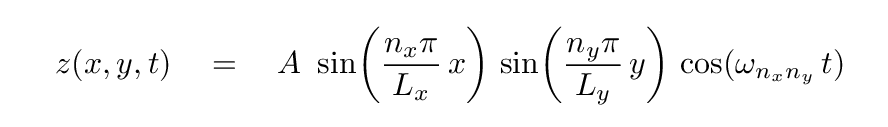
Q: So, how can we find out if our guess is correct?
Easy! All we have to do is check to see if it satisfies the 2-D wave equation. If it does, then since it does satisfy all the boundary conditions, it must be a valid way to describe the position of the plate at any position and time.
Here's the differential equation our guess ought to satisfy. Does it?
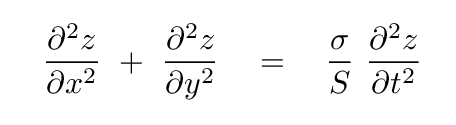
Q: What is the second derivative of z with respect to x? Q: What is the second derivative of z with respect to y? Q: What is the second derivative of z with respect to t?
The pieces are
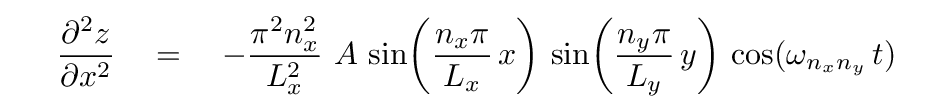
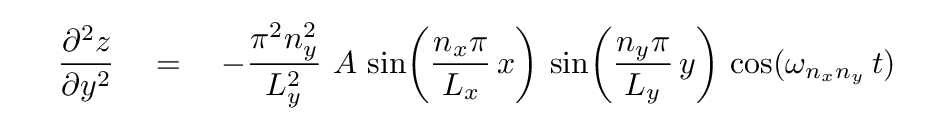
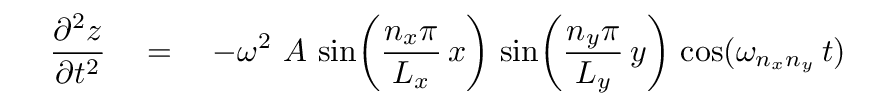
Fortunately, all three of these derivatives share a LOT of terms. When we plug them into the differential equation and cancel all the common terms, we end up with
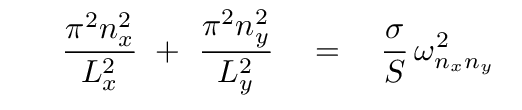
What does this mean? It means that our guesses do satisfy the differential equation, and will describe the displacement of the plate, as long as the frequencies of motion are given by
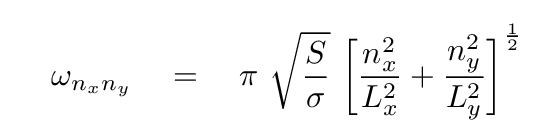
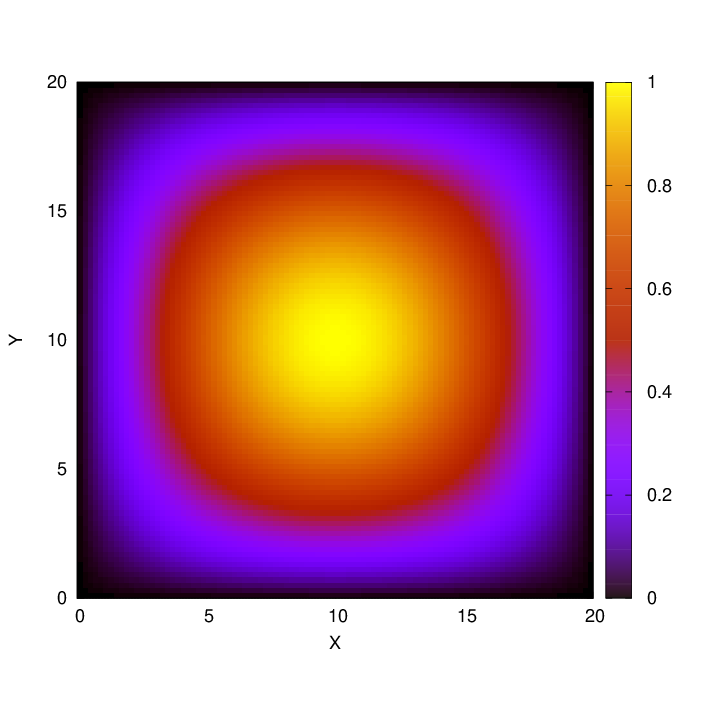
We have derived an equation which ought to describe the normal modes of oscillation of a rectangular plate clamped around its edges. We can compute the height of the plate at any position and time using that equation. If we choose just one moment in time, then it's not too hard to make pictures of the patterns.
For example, the pattern for nx = 1, ny = 1 looks like this:
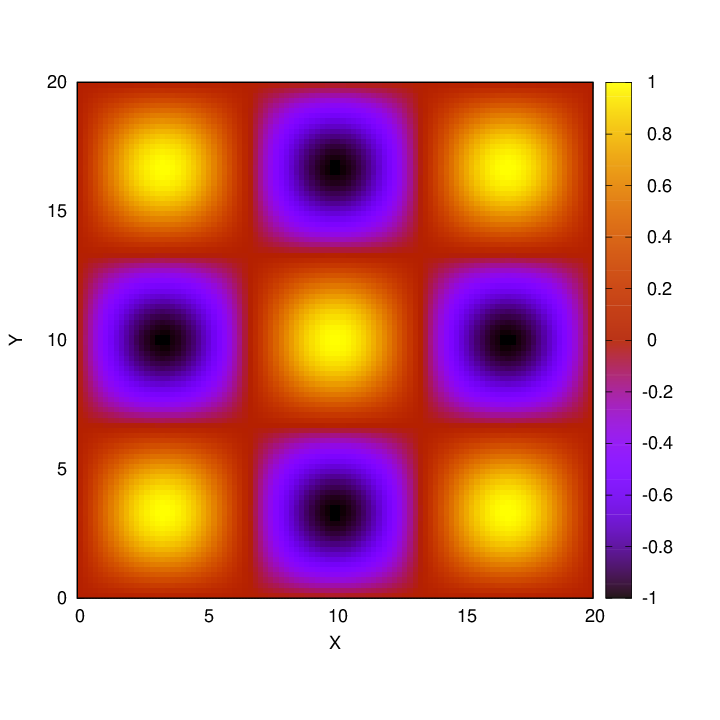
For nx = 3, ny = 3 we get
If the mode numbers are different in the two directions, the pattern becomes less symmetric. Below is nx = 2, ny = 5.
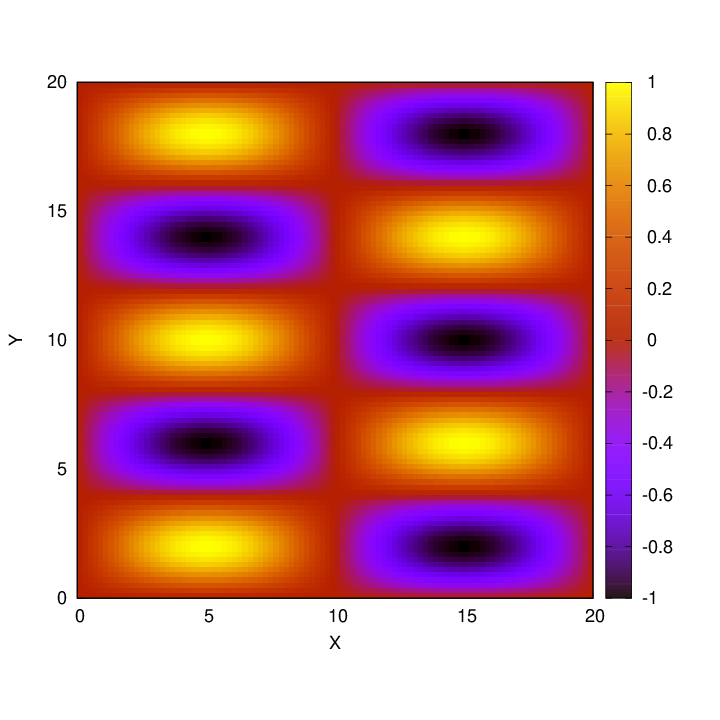
Is there any way to check our result?
Sure! Cut a rectangle out of a thin sheet of metal, clamp it around the edges, and then whack it in the middle. Watch carefully, and see if the miniscule vertical motions of the plate agree with our equation.
That's actually not a crazy idea. A very popular way to illustrate these concepts was invented by the German physicist and musician Ernst Chladni. He found that the teeny oscillations of a thin plate become easily visible if one scatters grains of sand or salt upon the plate. Regions which have large amplitudes of oscillation (antinodes) will shake the grains off and away, while regions with zero motion (nodes) will collect the grains.
Below are some modern examples of Chladni plates in action. Click on each image to watch a short video.
Yes, yes, I'm cheating a bit here. All the examples you see below, and most you can find online, leave the edges of the plates FREE, rather than fixed. The boundary conditions for plates free at the edges are quite a bit more complicated than those for plates clamped at the edges, so the form of the wave function and the solutions are quite a bit different. However, the idea of a series of resonant modes, in which the number of nodes increases with the frequency, is similar.
The video below shows clearly how to set up a plate for experiments.

Image and video courtesy of
Cymatics
I recommend pausing the next video at

Image and video courtesy of
brusspup
Let's look again at the equation for the frequency of the normal modes of a rectangular plate.
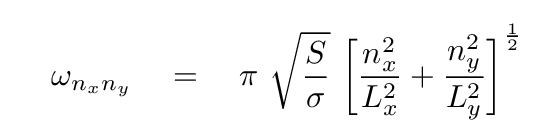
Note that for any particular size of plate, there may be several combinations of the mode indices which yield the same frequency.
For example, if a plate is square, so that Lx = Ly, then the combinations
If we make the plate a rectangle with Lx = 2*Ly, then
What does this mean? In the case of the second example, if we provide this particular frequency as an input, we might see the plate oscillate in the (4, 1) mode ... or we might see it vibrate in (2, 2) mode ... or it might switch from one pattern to the other, and then back again. We can't really be sure what we will see, because both patterns are excited by the same frequency.
Physicists describe this situation using the word degenerate:
The (4, 1) and (2, 2) modes are degenerate in frequency.
The idea of degeneracy -- that different states of a system might be produced by, or correspond to, identical values of some observable quantity (frequency, energy, angular momentum, etc.) -- turns up again and again in many situations. If you continue to take physics courses, you are bound to encounter lots of degeneracy.
What if the two-dimension plate isn't a rectangle, but a circle?
(Go to 0:55 in the video below)

Image and video courtesy of
Santa Barbara City College Physics
Using a Cartesian coordinate system (x, y) doesn't work very well in this case. Instead, we should pick one that matches the plate: polar coordinates (r, θ).
In these coordinates, our guess for a separable function might be
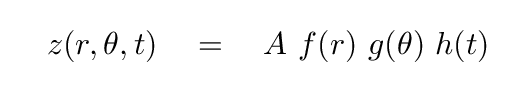
What would be good choices for these functions?
But what about the radial dependence? What sort of function do we need? If the plate is clamped around the edges -- like the membrane of a drum -- then the displacement at r = R will be zero. We might guess that the displacement might be largest near the center of the circle.
Q: What type of mathematical function is a good choice to describe
the radial dependence of a vibrating drumhead?
It should be largest near the center (r = 0), zero at the edge (r = R),
and permit some integer number of oscillations in between ...
well, it should probably decrease in amplitude with radius,
in general.
It turns out that a really good choice for this situation are the Bessell functions of the first kind!
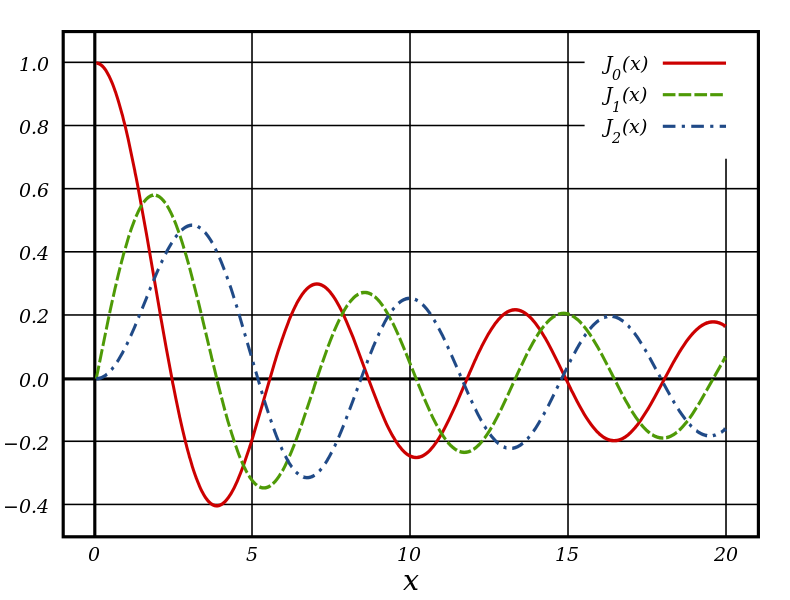
Image courtesy of
Inductiveload and Wikimedia.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.