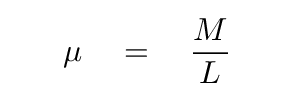
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Today, we return to the vibrations in a string stretched between two fixed posts; but this time, we will treat the string as a continuous medium, rather than as a collection of many discrete objects linked together by ideal springs. The big goal of this approach is to derive what is known as the wave equation.
Forces on a little section of string
Consider a piece of string, of length L and mass M, stretched between two fixed posts with tension T everywhere. The linear mass density of the string -- mass per unit length -- can be written as
If we displace the string slightly from rest, then release it, it will vibrate up and down, up and down.
We will zoom in and examine the properties of one tiny little section of the string. During our analysis, we will assume that all the vertical displacements are small compared to the length of the string -- which means that all the angles we will discuss are also small. We will also assume that all horizontal displacements are zero; the string may stretch and contract a bit, but it doesn't move left or right.
In the little section below, the tension of the string is constant everywhere, and has a value T.
This little section of the string stretches from position x to (x + Δ x). The angle of the string above the horizontal changes very slightly from the left end (θ) to the right end (θ + Δ θ).
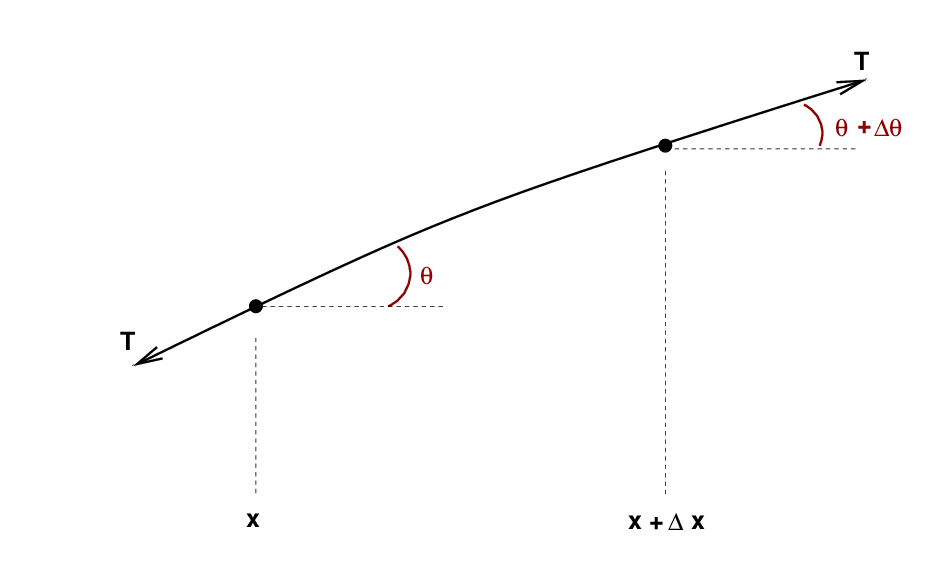
Q: There are two vertical forces acting on this little piece of string.
Can you quantify them?
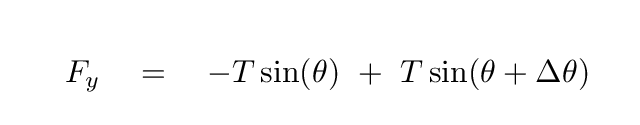
Now, if the angles are all small, then we can simplify a bit:
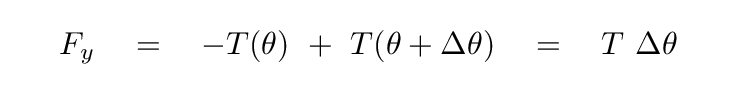
The force in the y-direction is, of course, equal to the mass of the little section times its acceleration in the y-direction. Because we are concerned with this little section only, at a fixed x position, we can use the partial derivative of y with respect to time; there is no change in x involved.
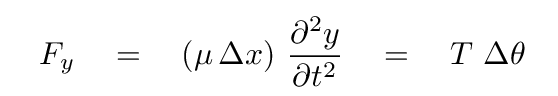
What about the term involving θ? Well, at this moment in time, the angle θ is the slope of this little section of string; by definition, that's the partial derivative of y with respect to x.
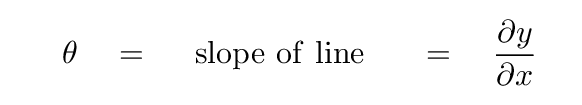
The CHANGE in this slope, as we move from the left-hand end of the little section to the right-hand end of the section, must be equal to the rate at which the slope changes with x, multiplied by the width of the section Δ x.
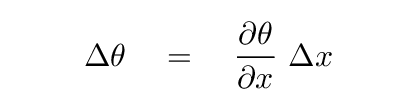
But if the slope is the derivative of y with respect to x, then the derivative of the SLOPE with respect to x must be
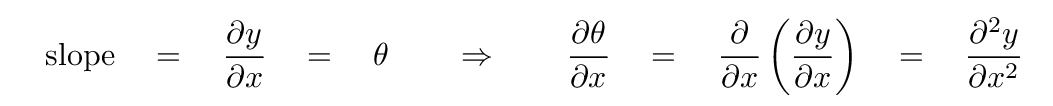
And so, putting the pieces together, we find that Newton's Second Law for the motion of this section in the vertical direction turns into
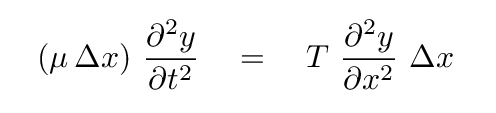
Or, rearranging a bit, so that the spatial derivative goes on the left-hand side,
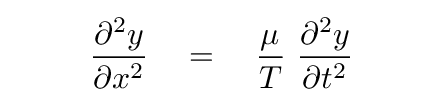
Well, well, this looks like quite a powerful relationship, connecting the second-order SPATIAL derivative in the y-direction to the second-order TIME derivative in the y-direction.
But can it be true? Do the units make sense?
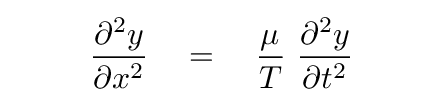
Q: What are the units on the left-hand side? Q: What are the units of each term on the right-hand side?
In the end, the units on both sides turn out to be (1 / length), so the equation does make sense.
Look at the first term on the right again. It has units of (time / length)2, which is equivalent to the one-over-velocity-squared. This is a clue that the speed of disturbances travelling along the length of a string -- horizontally -- will be given by the combination of terms
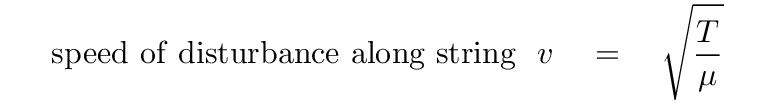
If we replace that term involving tension and mass density with a more general expression for speed, we end up with what is known as the wave equation:
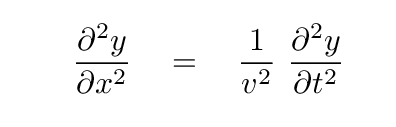
Although we have derived it by examining the properties of a string, this equation governs the motion and properties of all sorts of waves: light waves, sound waves, water waves -- you name it. The speed represented by the v term in the equation will be different for each particular type of wave, of course, but the relationship between SPATIAL and TEMPORAL derivatives remains the same.
Back to the motion of the string
Does this wave equation help us to figure out the motion of our little section of string? Yes, it certainly does.
Let's begin with one of our common assumptions: there are normal modes of the vibration, in which all sections of the string will oscillate with the same frequency. If we make that assumption, then the position of any little piece at location x along the string must be
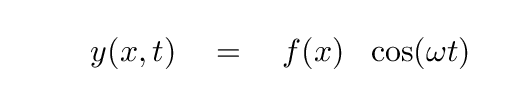
The wave equation tells us that there is a particular relationship between the second spatial and second temporal derivatives of the y-position of the string.
Q: What is the second derivative of this equation with respect
to position x?
Q: What is the second derivative of this equation with respect
to time t?
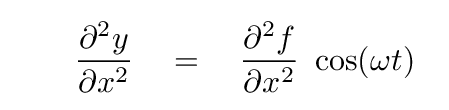
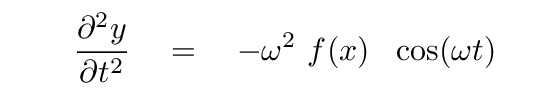
If we plug these derivatives into the wave equation, we get
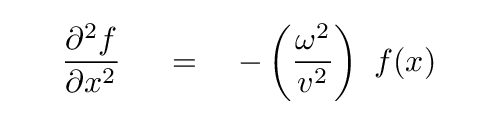
Oh, hey, that's familiar! We know how to solve this differential equation, don't we?
Q: What function f(x) solves the differential equation above?
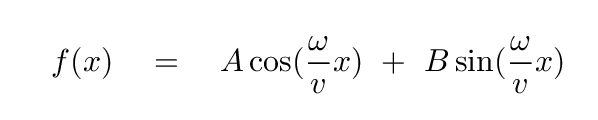
We can use the boundary conditions to pin down the values of the arbitrary constants.
The first condition forces us to conclude that A = 0.
The second condition requires that
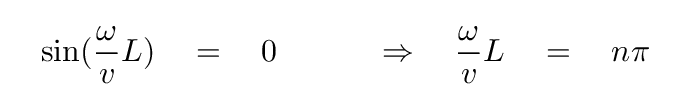
and so the ratio of angular frequency to velocity must be
So, using those boundary conditions, we know that the function describing the SHAPE of the string at any time must be
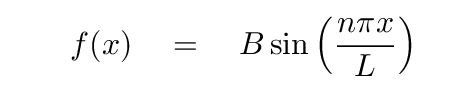
What about the FREQUENCY of the oscillations in the y-direction? Is there any way to figure out the frequencies of the normal modes?
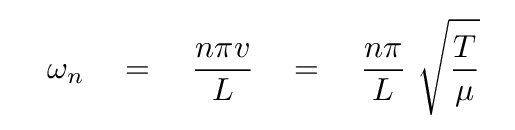
If we define the angular frequency of the fundamental mode, corresponding to n = 1, as
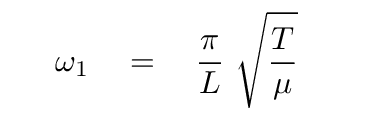
then the angular frequency of the higher (but still relatively low) order modes is given by
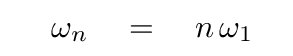
Putting the function describing the shape of the string together with the function describing its variation with time, we finally have
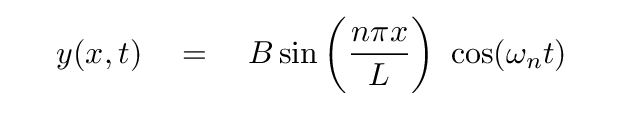
Let's use some of the information we've derived above to solve a simple, real-world problem: how tightly must we stretch a piano wire in order to generate the proper pitch?
Our goal is to produce a perfect middle C, which has frequency f = 261.6 Hz, when the wire vibrates in its fundamental mode. The wire inside the piano, made of high-tensile ASTM A228 steel, has the following properties:
Q: What is the desired angular frequency ω? Q: What is the linear mass density of the wire μ? Q: What is the required speed of a wave on this wire? Q: What is the proper tension?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.