Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Recall the main lessons from our previous lecture: when a travelling wave runs into a boundary, a REFLECTED wave may be created, which travels back toward the source of the incident wave. In order to determine the properties of this reflected wave, we looked to the boundary conditions.
In particular, a very common set of boundary conditions for the interface between two regions with different physical conditions is
Today, we will investigate a situation in which another boundary condition can apply.
You've seen what happens when a wave travelling along a string meets a wall, or when its meets an end which is free to move.
But what happens if a wave travelling along one string comes to a place where the string changes from one material to another? Is the wave reflected back along the original string? Or does it progress onto the new string? Or does it do both?
That's the topic for today: the possibility of transmission of a wave at this sort of a boundary between two strings -- or between two media, in the more general case. We'll stick with strings in these examples, but the results may be applied to other situations.
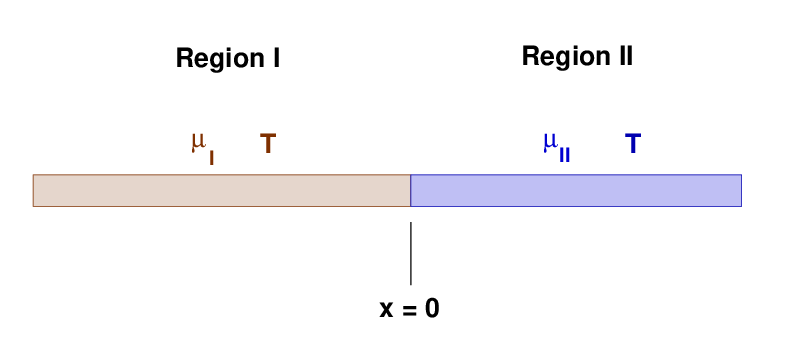
So, here's the picture:
The incident wave comes from the left-hand side, in Region I, on a string with linear mass density μI and tension T. When the wave reaches x = 0, it encounters a splice with a string which has a possibly different linear mass density μII, but the same tension T.
Does the wave move forward into Region II?
Our first step is to figure out the wave number associated with the wave in each region. One thing that MUST be true, on simple physical grounds, is that the angular frequency ω of waves on one side of a boundary must match the angular frequency of those on the other side. If the strings didn't oscillate at the same rate, then one would be going up while the other was going down -- and the strings couldn't maintain contact.
So, if the angular frequencies of the two waves are the same, that helps us to figure out the wave numbers of the two waves.
Q: What is the wave number of the wave in Region I? Q: What is the wave number of the wave in Region II?
This is pretty simple: we can calculate the speed of waves in Region I as
and so the wave number in Region I must be
Likewise, in Region II,
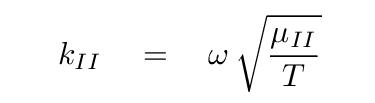
To summarize,
Let's send the incident wave (note the subscript i, for incident) towards the boundary from the far left-hand region of the rope. We can write its equation as
What will happen when this wave reaches the boundary between the two strings?
Nota bene: in many discussions of this topic, the wave equation is written in a slightly different manner, reversing the order of the "x" and "t" terms inside the function; something like this:
For consistency with earlier work, I'll continue to write functions of (kx - ωt). The ideas and math are exactly the same, but the values of the transmission and reflection coefficients may have a small sign change.
When the incident wave reaches the boundary, it MIGHT lead to
We can write equations for each of these possibilities as
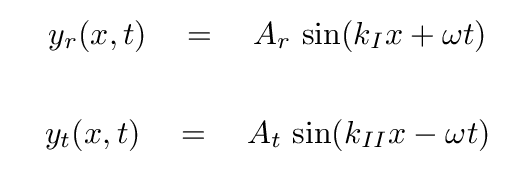
The $64,000 question is: "What are the amplitudes of the reflected and transmitted waves, in terms of the amplitude of the incoming wave?"
Well, if we know the boundary conditions, perhaps we can figure out a way to determine these coefficients.
Q: What are the boundary conditions we can apply at the meeting
of the two strings?
Good guess! The position of the strings must match,
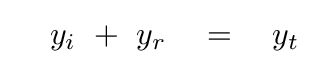
and the vertical velocities of the strings must match.
If either the position or velocity doesn't match, the strings will break.
Let's start with the first condition. At the boundary, where x = 0, matching the positions yields
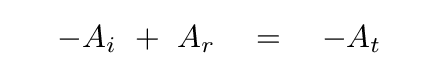
Good, good. This is one equation for two unknowns, but with a second boundary condition, we should be able to gain a second equation.
Let's look at the transverse velocities of each of the three waves.
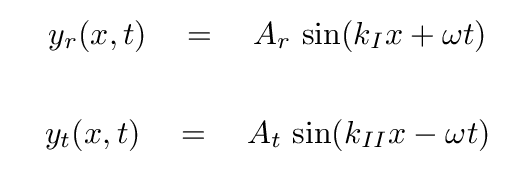
Q: Write down an equation stating that the transverse velocities
on each side of x = 0 are the same.
You should find
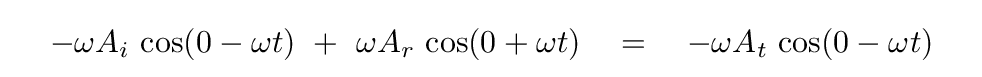
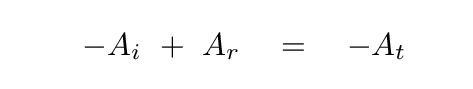
Wait a minute -- that's the same equation we derived by matching the positions of the strings! We haven't found any new relationship between the amplitudes at all!
Where can we find another relationship?
Looking closely at the junction of two pieces of string, we can come up with one more boundary condition: in order for the wave to pass smoothly from one region to another, the two pieces of string must have the same slope where they meet.
So, at x = 0,
Given our functions
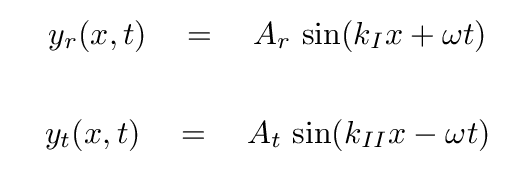
Q: Can you write this equation involving spatial derivatives
at x = 0?
The equation is
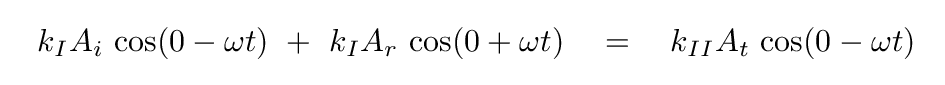
which simplifies to
Phew. That does provide a second relationship between the incident, reflected, and transmitted amplitudes.
Given these two relationships, a pencil, and a sheet of paper, one can derive the following amplitudes for the reflected and transmitted waves.
Have we made any mistakes? Do these amplitudes make sense? One way to check our work is to look at the results for some simple limiting cases.
What does our equation say in that case?
Q: What happens to the wave number in Region II, kII?
Q: What happens to the transmitted amplitude At?
Q: What happens to the reflected amplitude Ar?
The equations we derived at the very start of today's lecture show that wave number is proportional to the square root of linear mass density. So, if μII goes to infinity, so does kII.
Q: If the wave number kII goes to infinity,
what happens to the amplitude of transmitted waves?
The amplitude goes to zero! Just as our equation predicts. Hooray!
What about the amplitude of the reflected waves? We expect that the result would be the same as that for a string fixed in place, tied to a wall: Our analysis of that case concluded that the amplitude of the reflected wave was equal to that of the incident wave (but the phase was inverted).
What happens to the expression below when the wave number in Region II approaches infinity?
A judicious application of the binomial expansion shows that the amplitude of the reflected wave does, in fact, approach 1 times the amplitude of the incident wave. We end up with an equation for the reflected wave of
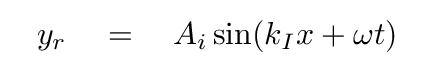
which (as we saw last time) corresponds to a wave with the same amplitude, but inverted phase, travelling back to the left.
Just as expected.
What does our equation say in that case?
Q: What happens to the wave number in Region II?
The wave number approaches zero as well.
Q: If the wave number kII goes to zero,
what happens to the amplitude of transmitted waves?
Q: If the wave number kII goes to zero,
what happens to the amplitude of reflected waves?
If we plug a value of kII approaching zero into our expressions, we find that
Once again, our equations got it right.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.