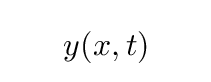
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
In an earlier lecture, we considered displacements from equilibrium of a long, thin string, stretched in the x-direction. Those displacements could be described as some function of the location along the string, and time.
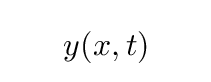
When we looked at the forces on a teeny section of this 1-D string, and compared them to the mass of the teeny section, we were able to derive a differential equation relating the second spatial to the second temporal derivatives.
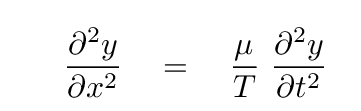
Note that this equation contains the ratio of an "inertial" quantity (the mass per unit length) to an "elastic" quantity (tension); the ratio is related to the speed of waves travelling down the string.
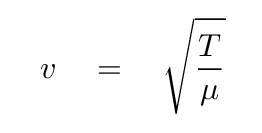
Fine.
Then, we added a dimension by considering displacements of a flat plate or membrane stretched out in the x- and y-directions. In this case, the displacements must be in the z direction, so we could describe them as
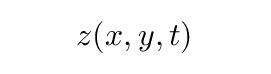
We analyzed the behavior of a teeny patch of this plate, comparing the forces on the teeny patch due to the displacements of the neighboring sections to the mass of the teeny patch. It turns out that one can derive another differential equation relating spatial derivatives to temporal derivatives -- but it looks a bit different.
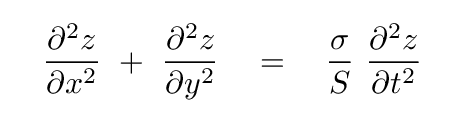
We see again the ratio of an "inertial" quantity (surface mass density) to an "elastic" quantity (surface tension); and, once again, this ratio is related to the speed with which waves travel across the plate.
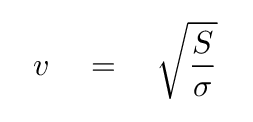
Dandy.
It's time to go for broke and allow the disturbances to travel in a 3-dimensional space.
Let's consider a rectangular box, with sides of length Lx, Ly, and Lz. Inside the box might be some medium, such as water or air, through which disturbances can travel; or it might be filled with a vacuum, through which electromagnetic waves might travel.
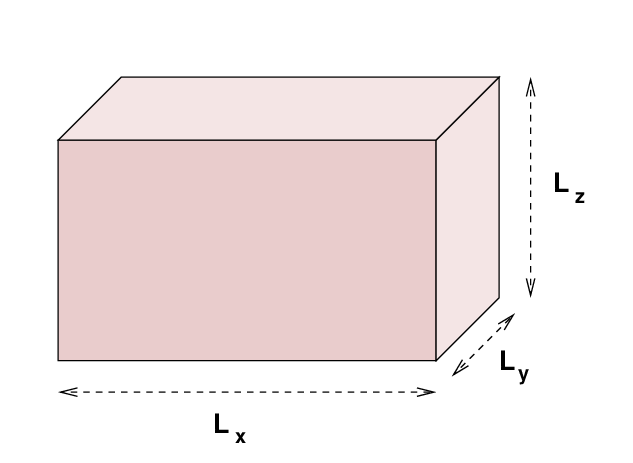
The disturbances might feature changes in pressure, or small oscillations in the positions of molecules, or the size and direction of the electric field. In a general sense, we can write there is some property of the space inside the box which undergoes small changes, as a function of location and time. We need the letters x, y, and z to describe positions inside the box, so let's use the letter ψ to describe the varying property.
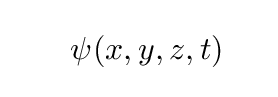
Suppose we zoom in on some teeny chunk of the region inside the box. If we compute the forces on this teeny chunk from the surrounding regions, and compare that to the mass of the medium within this teeny chunk
Yes, this method doesn't make sense if the box is filled with a vacuum, so one has to take a different approach to deal with electromagnetic waves; but the result will end up being very similar.
then we will find a very familiar relationship between the spatial and temporal derivatives:
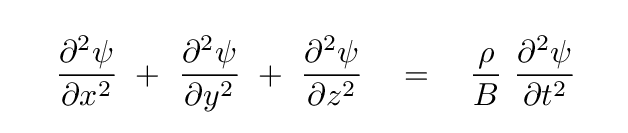
In this case, the coefficient on the right-hand side involves
Q: What are the units of bulk modulus divided by volume density? Q: Is there some physical significance to this combination?
Yes, of course, that ratio is the reciprocal of the square of the velocity with which waves travel through the medium.
Let's take a brief digression and see what this relationship tells us about the speed of (sound) waves through two familiar substances: air and water.
We'll need to know two properties of each substance. In the table below, I've listed representative values for each; they vary with temperature and altitude and so forth, so our calculations will only yield approximate results.
Can you fill in the speed of waves in each?
air water
---------------------------------------------------------------------
Bulk modulus (N/m2) 120* x 103 2.2 x 109
Density (kg/m3) 1 1000
Wave speed (m/s)
---------------------------------------------------------------------
The speed of waves through a medium will be large for "stiff" materials, and for materials with low densities. In general, waves tend to move more quickly through solids than through liquids or gases.
The wave equation in three-dimensions and Cartesian coordinates can be written as
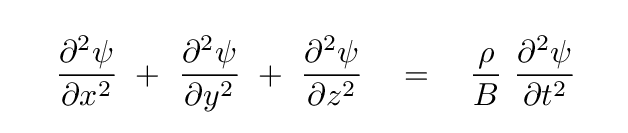
Now, that particular combination of second spatial derivatives appears not only in the wave equation, but also in many other branches of physics and mathematics. In fact, it appears so frequently that scientists have created a special symbol to simplify writing expressions. The symbol ∇, called "del" or "nabla", is defined as
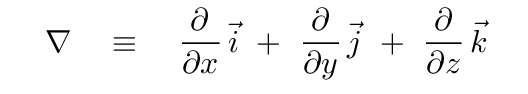
That means that the sum of the second derivatives can be written using the operator squared -- which is called the "Laplacian" --
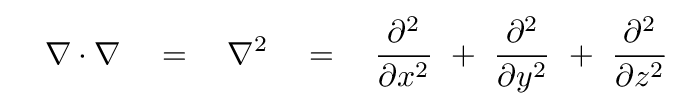
like so:
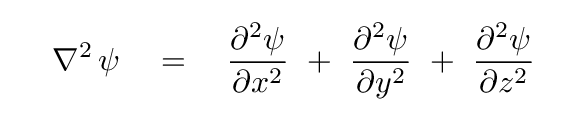
And thus the wave equation can be written in a very compact form:
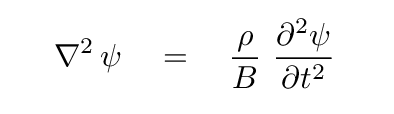
Enough with sound waves travelling through air or water. It's time for some good old electromagnetic waves, travelling through a vacuum (or ordinary air, which is close enough to a vacuum for today's purposes). For electromagnetic waves, one can derive a wave equation which looks just a bit different from the one we saw earlier; but it MUST look different, because a vacuum doesn't have a density, after all.
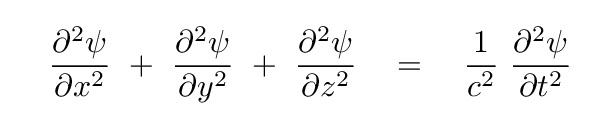
If the electromagnetic waves are confined within a rectangular metal box, like this,

then the boundary conditions are that the value of the electric field ψ must be zero along every surface.
What functions of ψ
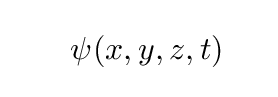
will satisfy both the boundary conditions and the wave equation?
Hmmm. It surely would be convenient if the functions turned out to be separable, so that we could write individual functions of x, y, z, and t alone.
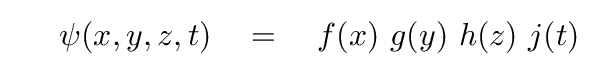
Q: Can you guess what these separable functions might look like?
If you've been paying attention for the past few weeks, you will likely have guessed that sinusoidal functions of position and time might be good choices. For example,
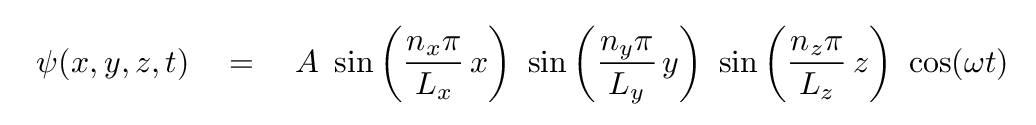
The normal modes of this system will satisfy this equation, which allows us to solve for the frequencies of these normal modes. All we do is plug this guess at ψ into the wave equation, and solve for the angular frequency ω.
The three spatial derivatives are
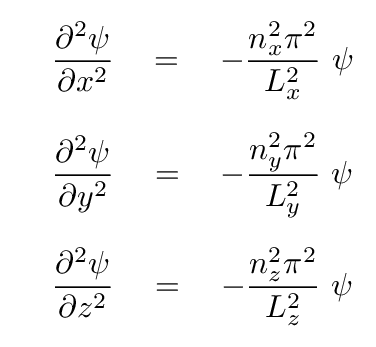
while the time derivative is
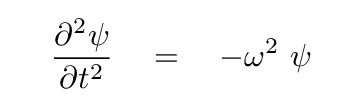
Inserting these expressions into the wave equation,
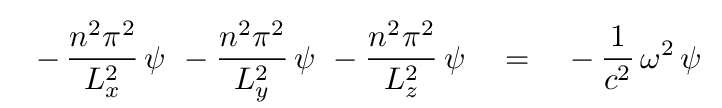
we can solve for the angular frequency of any particular combination of modes nx, ny, nz.
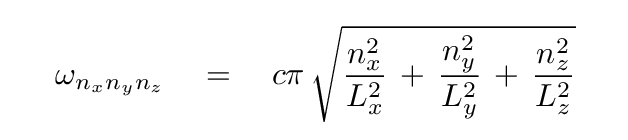
Q: I line an cardboard box with aluminum foil.
Its dimensions are
Lx = 80 cm
Ly = 60 cm
Lz = 40 cm
What is the frequency (in Hz) and wavelength of the
fundamental resonant mode inside this box?
You should find
This corresponds to the radio portion of the electromagnetic spectrum. In particular, to the region used to send television signals, somewhere in the UHF region (for those of you old enough to know what that abbreviation means).
If you can remember seeing rabbit-ear antennae on an old TV set,

you'll recall that they are -- surprise, surprise -- roughly the size of a cardboard box, to within factors of two or three.
Yes sirree bob, those old-timey television sets (and even the new digital ones) receive radio waves which are about the same size as penguins.
Speaking of rectangular boxes with conducting walls inside of which electromagnetic waves bounce and bounce, have you ever heard of "microwave ovens?"
These handy devices shower food with electromagnetic waves, heating the food quickly and conveniently. The frequencies used by most ovens lies in the range
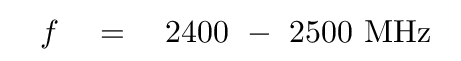
Q: What is the wavelength of an electromagnetic wave of this frequency?
Perhaps the photograph below will help. It shows a chocolate bar which was zapped for 4 minutes inside a microwave oven. The scale bar below is marked in centimeters.

Image courtesy of Mr. Muskopf. Thanks!
This is ... a bit too small for practical use. So most microwave ovens are boxes roughly 25 - 35 cm on a side. In order to achieve normal modes -- resonance -- inside such a large box, we need to pick values for the indices nx, ny, nz, which are larger than 1.
If one chooses just the right ratios of length-to-width-to-height, then one can cause SEVERAL different combinations of modes to have frequencies which fall into this narrow range of 2400 - 2500 MHz.
Hmmm. Several different modes which end up with
nearly the same frequency.
Q: What word to physicists use to describe such a condition?
Degenerate, of course!

For example, consider one particular brand of microwave oven. It has dimensions
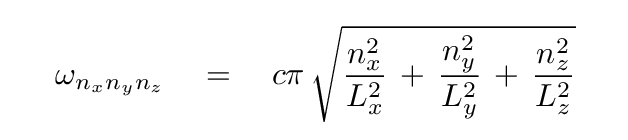
Q: What is the angular frequency ω for waves with
nx = 4, ny = 3, nz = 1?
What is the frequency in Hz?
Q: What is the angular frequency ω for waves with
nx = 2, ny = 4, nz = 3?
What is the frequency in Hz?
The combination nx = 4, ny = 3, nz = 1, will yield a 2414 MHz, inside the desired region.
But the combination nx = 2, ny = 4, nz = 3, leads to a frequency of 2433 MHz, which also lies in the region.
Thus, a device which creates microwaves with some spread around 2450 MHz will cause some of those waves -- not just one particular frequency, but waves with several frequencies -- to resonate inside the cavity, building up energy which can eventually be transferred to food. That's more efficient than a setup which has only a single, very pure, resonant frequency.
Q: Can you find any other combinations of modes which
create waves which will resonate inside this oven?
If you can, why not get some credit for your work?
We've discussed the propagation of waves in three dimensions in one particular case: when the boundaries of the system are rectangular. But what if there are no boundaries? What if a bird flying in mid-air chirps, or a firefly emits a brief pulse of light? The sound or light waves emitted are free to travel in ANY direction.
In a case like this, the waves will spread out in a series of ever-expanding spherical shells. In order to describe this sort of propagation, it is convenient to introduce the spherical coordinate system.
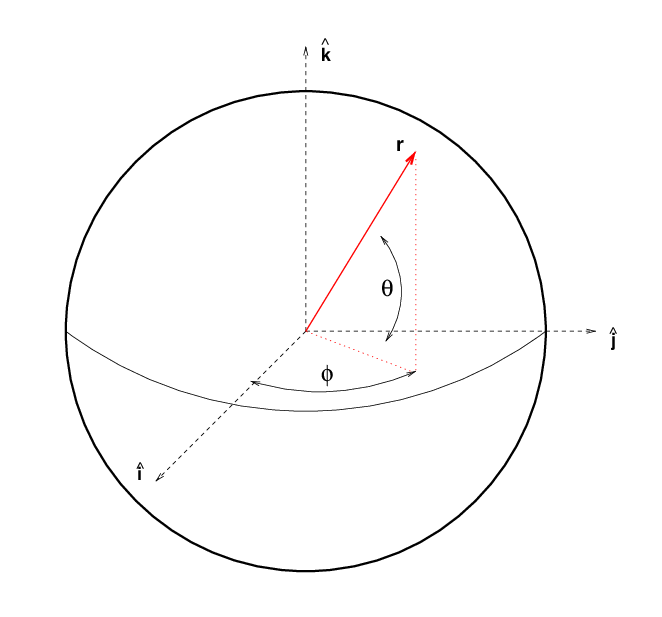
We must now describe the pressure of a sound wave, or the electric field of a light wave, as a function of these spherical coordinates:
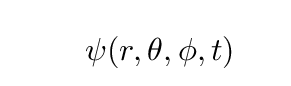
In the case of perfect spherical symmetry -- such as the pulse of light from a firefly high above the ground -- the wave equation turns into
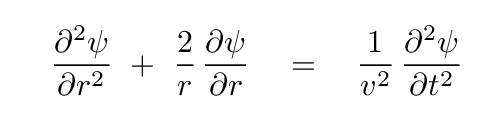
Q: Does the following function satisfy the purely spherical wave equation?
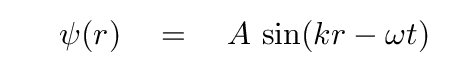
Q: How about this one?
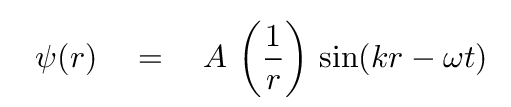
Yes, that one does work. Phew.
So, the solution to a spherically expanding wave can be written in the form
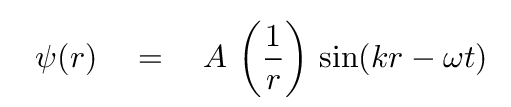
What happens to the amplitude of this wave as it moves away from its source, and r increases?
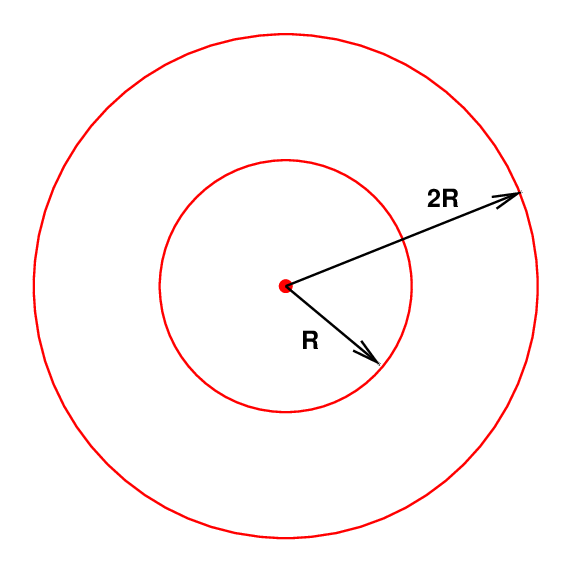
As the radial distance doubles from R to 2R,
In other words, the total energy carried by the wave remains constant as the wave expands, but the energy per unit area -- a quantity sometimes called "flux" -- decreases with the square of the radial distance.
Q: Is there a common phrase describing the phenomenon of the flux
from a point source decreasing as the square
of the radial distance from the source?
Yes, there is: it's just another aspect of the inverse square law.
Now, in the more general case, if there is some dependence on the altitude angle θ or azimuthal angle φ, then the wave equation becomes ... rather scary.
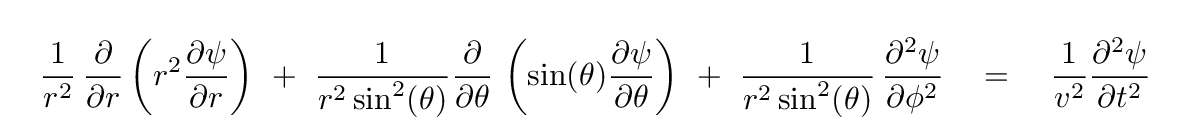
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.