Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
We've been playing with string for many days. Let's switch to a different medium, and a slightly different type of disturbance. We will examine the behavior of longitudinal waves moving through a long, thin rod. Unlike the transverse waves on a string, longitudinal waves involve the oscillation of material along (and against) the direction of motion of the disturbance.
You should see our new pal the wave equation show up as we examine the response of a little section of the rod to a perturbing force ...
Forces on a little section of a rod
We're going to use two different variables in the following discussion, both of which describe in some way the position of a little section of a rod along the x-axis. Let us therefore define very clearly the meaning of each one before we start.
Consider a long, thin rod of material, with cross-section area A and density ρ. We'll concentrate on the properties of a little section of the rod which runs from position x to (x + Δ x).
Q: What is the mass of this little section?
Right.
Now, we exert a force on one end of the rod. How does it respond?
The rod stretches in response to the force. The amount by which the rod stretches depends on how far from the end one looks: the closer to the end with the force, the bigger the change in length.
Let's call the change in the position of any point on the rod z. The closer to the right end of the rod, the bigger z is. At the position of the left-hand edge of our section, x, the material deforms by z; but at the right-hand edge of the section, the material deforms by a slightly larger amount (z + Δ z).
In other words, our little section not only translates to the right, but becomes slightly longer, too.
Why does the section elongate? Because the force pulling on its right-hand side is slightly bigger than the force pulling on its left-hand side. In other words, F2 > F1.
Stress, and the reaction to it: strain
You may recall that physicists use the term stress to describe the differential force acting on the two ends of a little section of an object.
In response to the stress on an object, it may change its shape; this response is called the strain.
For many objects, these two phenomena -- the stress on an object and the resulting strain -- are related in a simple manner, at least when the changes in shape are very small compared to the original size of the object. In general, the stress is equal to some elastic modulus multiplied by the strain. When the object is long and thin, and being stretched along its length, this coefficient is called Young's modulus. It is usually labelled with either Y or E.
The left-hand side of this boxed equation has the net force on the little section, divided by area. That net force, by Newton's Second Law, is just the mass of the section times its acceleration in the direction of the rod's length. In other words, the acceleration in the z direction.
So the left-hand side becomes
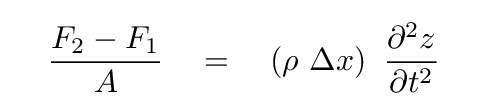
Now, here comes the tricky part. On the right hand side of the boxed equation, there is a term for the change in z divided by the change in x. How large is the change in the stretched distance, Δ z, over the length of our little section? One way to calculate is as the rate at which z is changing with x, multiplied by the width of our little section:
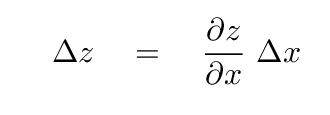
This should remind you of a similar mathematical technique we called upon in our previous class meeting, when discussing the change in slope of a vibrating string.
When all the distances involved are very small, and we restrict ourselves to a fixed moment in time, we can write this using the second derivative of z with respect to x.
The differential equation of motion
So, if we use these relationships, Newton's Second Law for the motion of this little section of the rod turns into
Putting this into the standard form, with second SPATIAL derivative on the left and second TEMPORAL derivative on the right, we end with the wave equation for longitudinal waves travelling down a long, thin rod. Remember, z is defined as the displacement of some tiny piece of the rod away from its equilibrium position; it runs parallel to the x-direction.
Q: What is the speed of these waves?
Yes, the speed of the waves is given by
As you might guess, there are certain special modes -- normal modes -- of vibration in which all parts of the rod oscillate with the same frequency ω. What are the frequencies corresponding to these modes?
In this case, the easiest way to find them is to skip the mathematics and look at the physical situation. Suppose that we clamp one end of the rod, holding it perfectly still and preventing it from vibrating. The material throughout the rest of the rod may vibrate, and the material at the right end of the rod is free to vibrate as well.
In this case, any oscillations must have amplitude zero at the left (clamped) end of the rod, but maximum amplitude at the right (un-clamped) end of the rod. The lowest normal mode, aka the fundamental mode, must therefore have an amplitude which looks like this. In the figure below, the vertical position of the green line away from the mid-point of the rod denotes the amplitude of the horizontal motions. Yes, it's awkward to try to draw longitudinal vibrations.
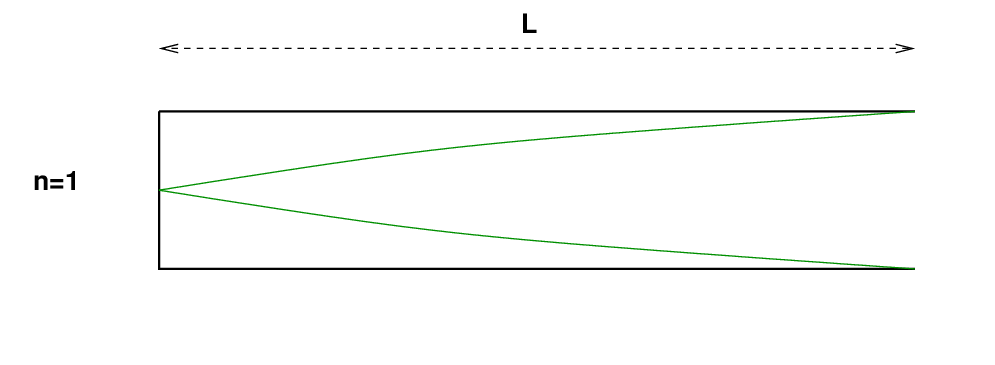
Q: What is the wavelength of the n=1 mode?
In the n=2 mode, the amplitude at each end is the same -- zero at left, maximum at right -- but there is now one additional node in between.
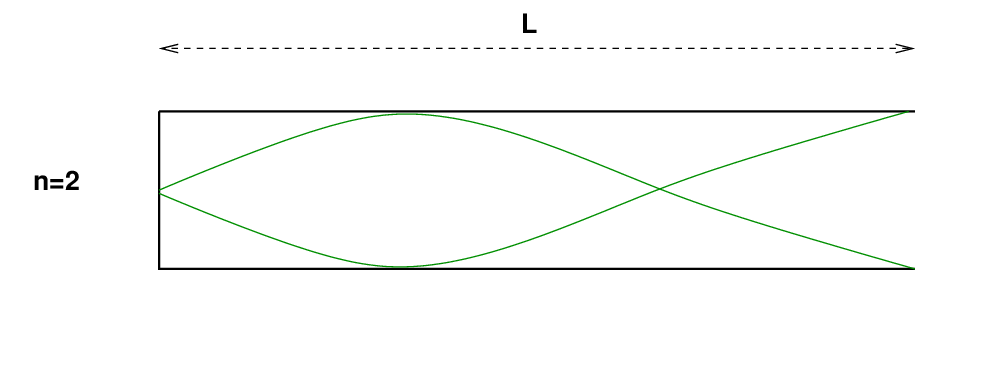
Q: What is the wavelength of the n=2 mode?
In the n=3 mode, there is one more node in the middle.
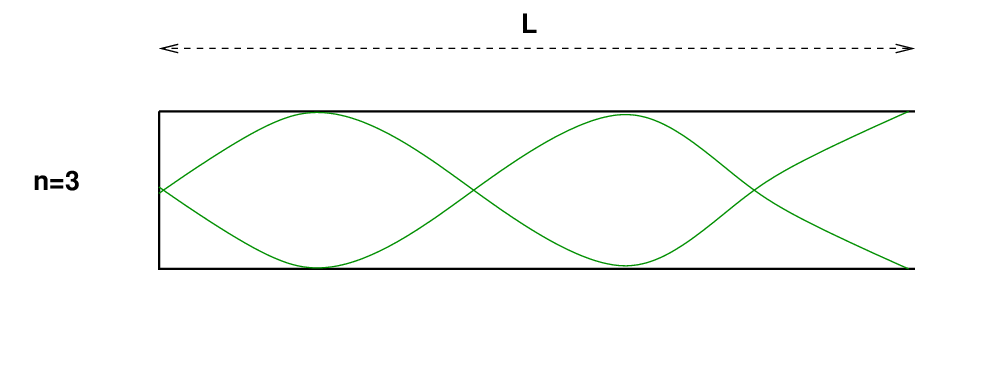
Q: What is the wavelength of the n=3 mode?
Q: Can you derive an equation for the wavelength of the
n'th normal mode?
Q: Can you derive an equation for the frequency of the
n'th normal mode?
You should end up with
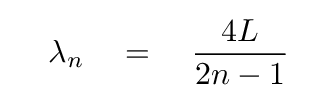
and
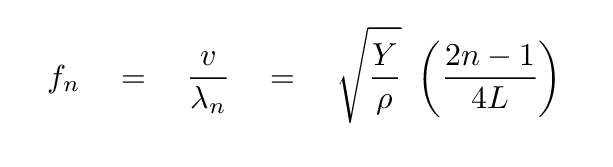
This time, let's hold the rod at its middle, rather than at one end. Now, the amplitude of oscillation must be zero at the center of the rod, but must be a maximum at both ends.
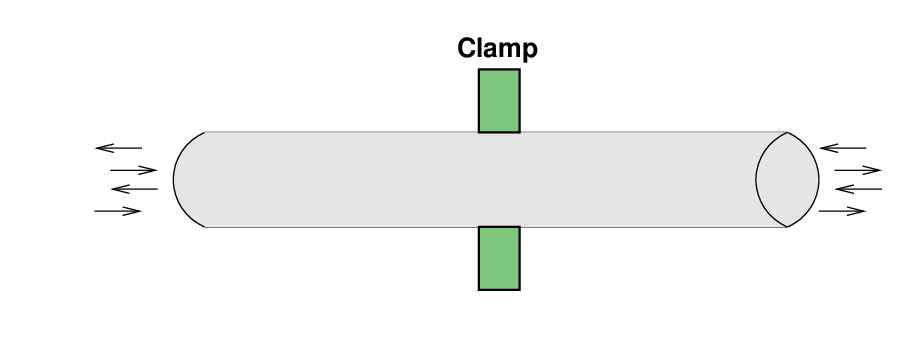
This means that the fundamental mode of vibration looks like:
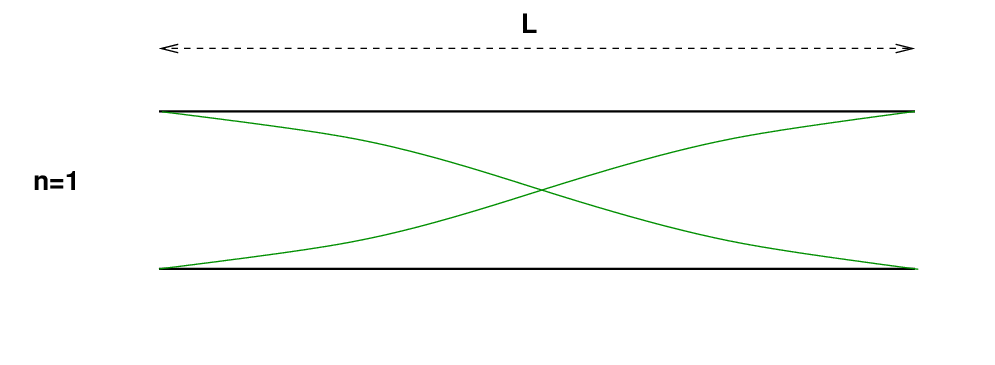
Q: What is the wavelength of the n=1 mode?
In the n=2 mode, the amplitude at each end is the same -- zero at left, maximum at right -- but there is now one additional node between each end and the middle.
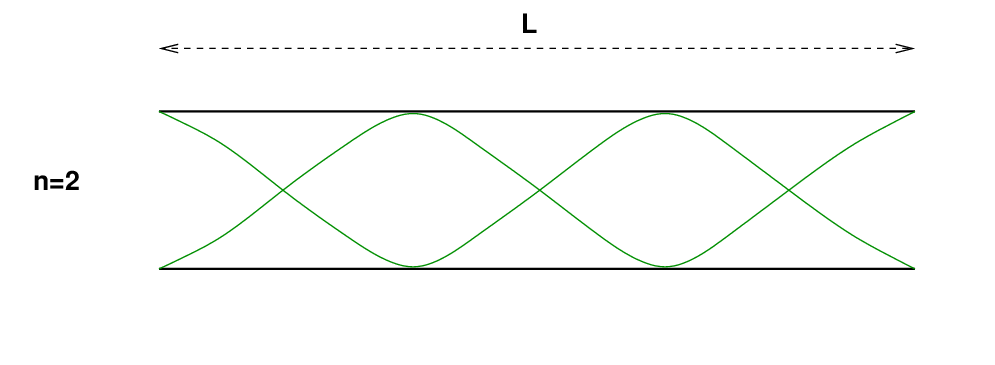
Q: What is the wavelength of the n=2 mode?
In the n=3 mode, we add another node to each half of the rod.
Q: What is the wavelength of the n=3 mode?
Q: Can you derive an equation for the wavelength of the
n'th normal mode?
Q: Can you derive an equation for the frequency of the
n'th normal mode?
You should end up with
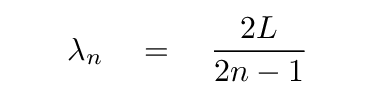
and
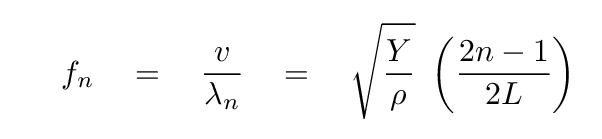
I have in class a long, thin rod of aluminum. The properties of this rod are:
length L = 91.1 cm
density ρ = 2700 kg/m^3
Young's modulus Y = 69 x 109 N/m^2
Can you figure out the answers to the following questions?
Q: What is the speed of waves travelling through the rod?
Q: If I hold the rod in the middle and ring it,
what frequency of sound will we hear?
Q: If I hold the rod at 1/4 of the distance from left
to right, and ring it, what frequency of
sound will we hear?
Q: If I hold the rod at 1/3 of the distance from left
to right, and ring it, what frequency of
sound will we hear?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.