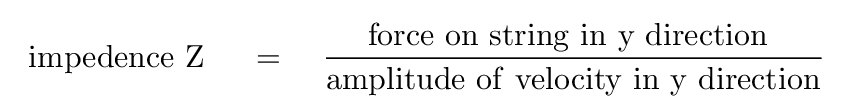
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
In ordinary English, the word impede has the following definition:
To stop in progress; obstruct; hinder
The word's origin, in Latin, refers to "entangling the feet."
This meaning transfers broadly into the jargon of physics. Impedance is a measure of the degree to which something is prevented from moving forward. In the world of electrical circuits, current is the quantity which is being prevented from progressing (and we'll come back to that later). In the world of strings and waves, however, the important item is the transverse velocity of the string.
In particular, physicists define the impedance of a system which sends waves down a string in the following manner.
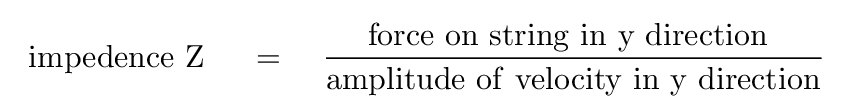
Or, in short,
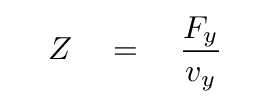
Imagine that we start with a long string, stretched under some tension. We can create waves by attaching a motor to one end of the string, pulling and pushing it with some frequency. Those oscillations will propagate down the string, carrying some of the energy of the motor to the other end of the string.
A system with large impedance will require us to pull the string with a large force in order to give the string some particular transverse velocity; a system with small impedance, on the other hand, will require only a small force from the motor to create the vertical motions of the same speed.
In this context, impedance sounds a bit like inertia. So we might expect that the linear mass density of the string will be involved in the calculation of impedance.
It might also remind you a bit of this equation from the past:

In a damped harmonic oscillator, there is also some connection between the force applied to a system, and the resulting speed of oscillation.
Okay, now that we know how impedance is defined, let's try to calculate its value for some simple string system. We'll begin with a string of linear mass density μ stretched with tension T. Near one end of the string, we place a motor with a small arm that attaches to the string. When the motor turns, the arm moves up and down, imparting some force F at a fixed frequency to the string. As a result, the string moves up and down with some particular vertical velocity vy; in addition, a wave moves to the right along the string, away from the motor.
The diagram below shows a little section of the string next to the arm which provides the driving force. Consider the point P on the string.
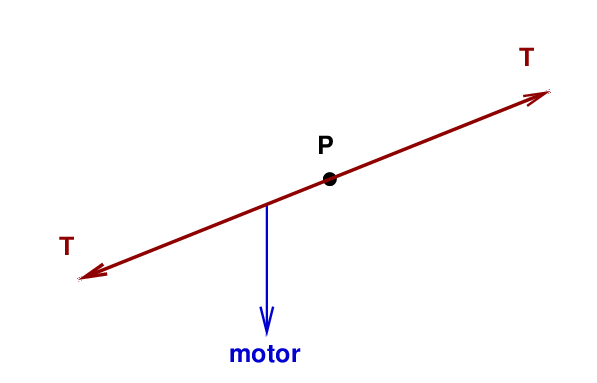
At point P, the tension in the string can be broken into horizontal and vertical components. We need to find the vertical force Fy in order to calculate the impedance.
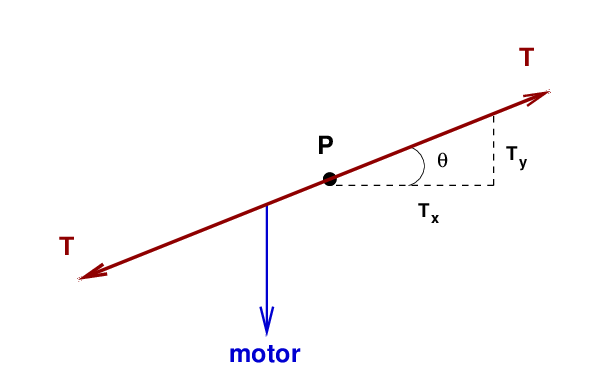
The magnitude of the vertical force is simply the vertical component of the tension.
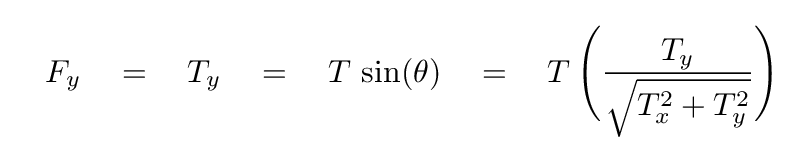
Now, as long as the string deflects by only a small angle (meaning that all vertical motions are much smaller than the length of the string), then the ratio of the vertical to horizontal components is approximately

Therefore, we can express the magnitude of the vertical force as
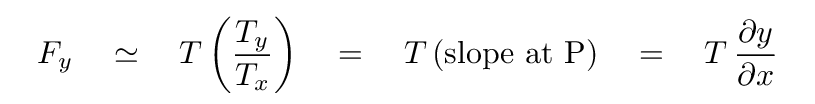
If one looks at the picture again, we can see that at this moment, the vertical force exerted on the string by the motor is downwards, or in the negative y direction; but the slope of the string is positive, so
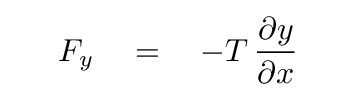
Let's assume that the position of the string is given by our old friend

Q: Write an expression for the force in the y-direction.
Right.
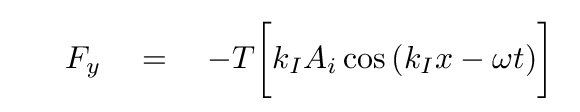
Okay, so that's the force.
In order to compute the impedance, we also need to know the speed of the string in the transverse, or vertical direction.
Q: What is the speed of the string in the vertical direction?
Yes, the vertical speed is the derivative of position with respect to time.
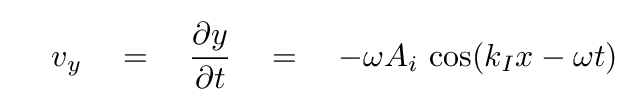
We can put these two expressions together to compute the impedance of this section (Region I) of the string.
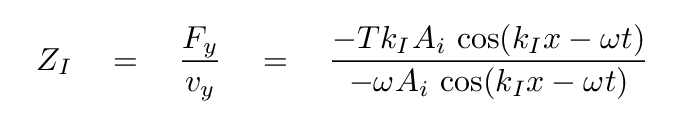
Some of the terms cancel, leaving us with tension times wave number, divided by angular frequency.

But that combination of wave number and angular frequency is related to the velocity of the wave ALONG the string (not transverse to it), so
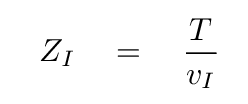
The velocity of waves travelling along this section of the string also depends on tension
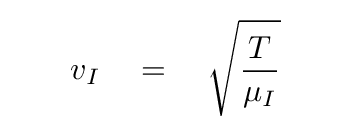
and it turns out that the mechanical impedance of a long string depends on two things: its tension, and its linear mass density.
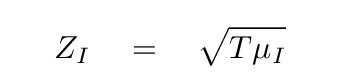
Let's see if this makes any sense by considering the limiting cases.
Yes, that make sense.
That makes sense, too.
More tension leads to smaller vertical motions, which means higher impedance. Yes, that sounds correct.
The really interesting aspects of impedance occur when we consider the boundary between two different pieces of string. Suppose we have two pieces of string with identical tensions, but different linear mass densities.
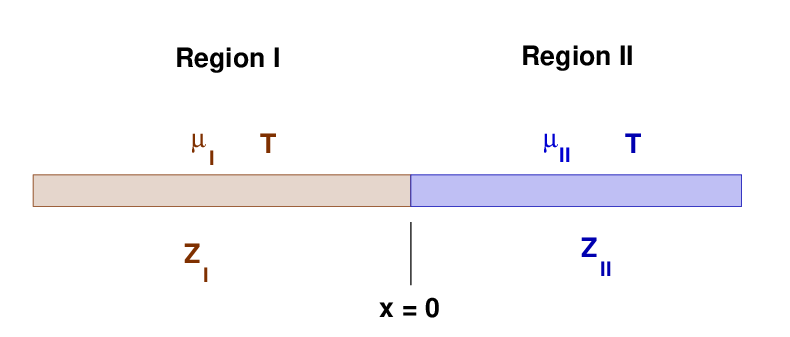
What will happen if a travelling wave from Region I

reaches the boundary?
As you may recall, we concluded last time that the coefficients of the reflected and transmitted waves are given by the expressions
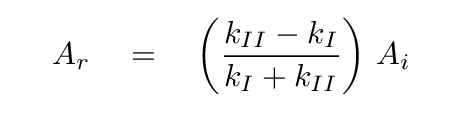
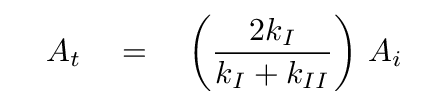
But since the impedance is directly related to the wave number,

and since the tension and angular frequency are the same in both regions, we can simply replace the wave number k in each region with the impedance Z for that region:
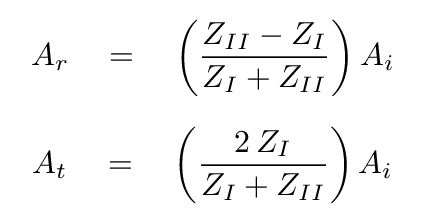
So, now we know how the change in impedance at a boundary between two strings is related to the coefficients of the reflected and transmitted waves at that boundary.
Suppose we send a travelling wave

moving along a string of impedance ZI, so that it approaches a boundary with a string of impedance ZII.
Q: If we want to transfer as much energy as possible to
the new string, in Region II, what value should
the impedance ZII have?
a) ZII should be (nearly) zero
b) ZII should be (nearly) infinite
c) ZII should be somewhere in between
The answer is not a), but c). In fact, the best choice for the impedance in Region II is

Why? Let's consider several cases.
First, the coefficient of the REFLECTED wave is not zero, but negative one times the coefficient of the incident wave. The amplitude of the reflected wave is the same size as that of the incident wave --- so it carries all the energy of the incident wave back, away from Region II.
Remember that the energy carried by a wave depends on several factors. One expression is

Yes, if the impedance in Region II is close to zero, then the coefficient A will be large; but a very small impedance also means (for our fixed tension) that the linear mass density must be very small. As the linear mass density approaches zero, the power carried by any wave through this medium must also approach zero.
No energy will move into Region II in this case.
Qualitatively, the string doesn't change at all at the boundary, so ... there is no boundary. The incident wave just keeps travelling to the right, into Region II, carrying all its energy.
Quantitatively, the expression for the reflected coefficient goes to zero, and the expression for the transmitted coefficient goes to one.
The maximum transfer of energy occurs NOT when the impedance in Region II is zero, but when the impedance values are the same on both sides of the boundary, a condition called impedance matching.
One can find analogous situations in other sorts of systems. There's a good list in Transverse Waves by David Morin. I'll list just a couple.
Would it help to place the patient and device into a vacuum chamber? In a gas of very low density, the speed of the sound waves would be faster than in air -- but the energy transferred by those waves to the skin and tissue would be very much smaller. So decreasing the "resistance" of the air to sound waves would not help.
In order to minimize reflections, technicians spread a special gel on the skin, then push the device into the gel. This removes the device-air interface, and replaces it with device-gel and gel-skin boundaries. The gel is specially designed to have impedance which is similar to both the device and the skin.
In between these two extremes will be some particular gear setting which maximizes the speed of the bicycle for the rider's leg motions. Choosing the right gear is equivalent to matching the impedance of the rider and the wheels.
The examples so far have assumed that the tension in the two strings is identical ... but that doesn't necessarily have to be true. Although it seems a bit awkward, one can imagine setting up equipment which would allow two strings to have different tensions, yet remain connected in a physically meaningful manner. All it takes is a ring sliding without friction along a vertical pole.
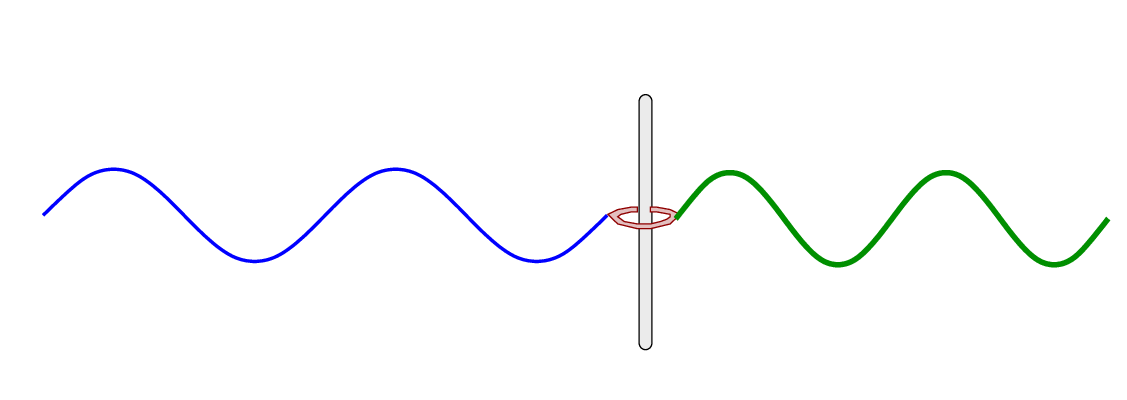
If we are allowed to change both the linear mass density μ and the tension T, then we can devise two strings with quite different properties which end up yielding the same impedance; all it takes is
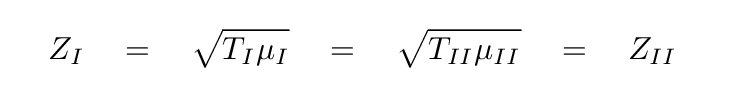
In fact, it is even possible to create a boundary with no reflection between a string and ... a pool of liquid. Huh?
No, it's true. As mentioned earlier, one can view the impedance of a mechanical system as the ratio of the tranverse force on a medium to the transverse velocity of the medium. Suppose that we place the end of a string into a pool of water, or oil, or some other liquid. When a travelling wave reaches the end of the string, it causes that end to oscillate by exerting a force in the transverse direction on the string; that force leads to some particular tranverse velocity.
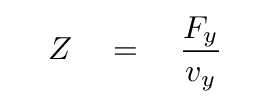
Objects which move through any liquid will experience a force opposing their motion, the liquid equivalent to air resistance. In many cases, this resistive force is linearly proportional to the speed of the object.
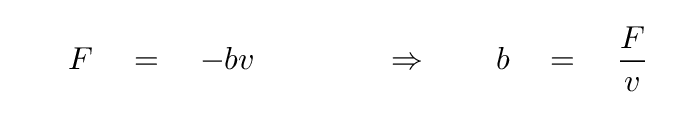
So, if we choose a liquid which happens to have a resistive coefficient b which is exactly the same as the impedance of the string
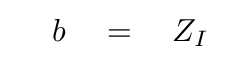
then the wave will transfer all its energy into the pool of liquid.
We've been discussing mechanical impedance, but the concept is a very important one in the area of electric circuits as well. In that case, we are still interested in a ratio of a "driving force" to some sort of "velocity", but the quantities are a bit different.
So, in the case of a direct-current circuit, the impedence is simply
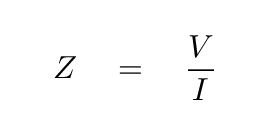
Q: Is there a more common name for impedance in a direct-current circuit?
Sure -- we just call it "resistance."
But when the voltage varies with time, as in an AC circuit, this relationship can become much more complicated. Electrical devices such as inductors and capacitors interact with time-varying voltage in particular ways; yes, the current usually does change over time, with the same frequency as the voltage; but not always at the same time.
In other words, in AC circuits, one must pay attention to the phase of the quantities, as well as to their amplitudes. The topic becomes rather complex, and it's one in which I have very little experience or knowledge.
But one thing that IS the same as in our mechanical system is that the flow of energy between circuits can be maximized by matching the impedance of the circuits at their junction.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.