Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Suppose we suspend a small light bulb from the ceiling of a huge building -- the hanger for a giant airplane, for example. When we send electricity through the bulb, light waves will fly outward in all directions: up, down, left, right, forward, back.
We can represent the light waves emitted by the bulb by drawing spheres (or circles, in my primitive 2-D picture) at the locations of the maximum amplitude of the electric field. As time passes, each sphere will expand outward at the speed of light.
If we try to measure the properties of this light at distances which are "close" to the source, we will find that it is rather complex.
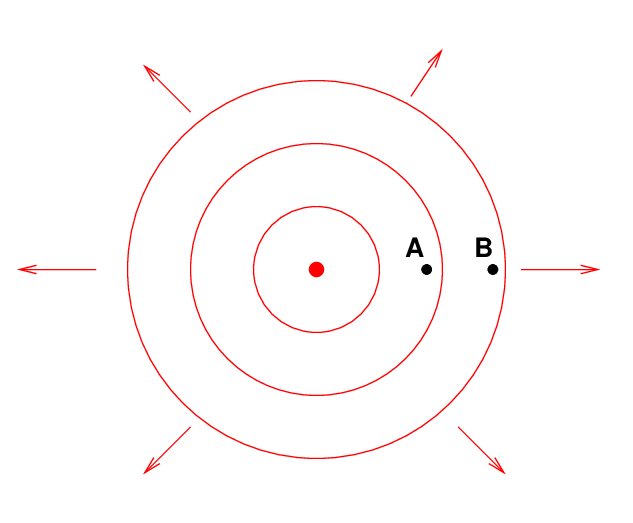
If we move our sensor just a little farther from the bulb, from A to B, the intensity of the waves changes significantly.
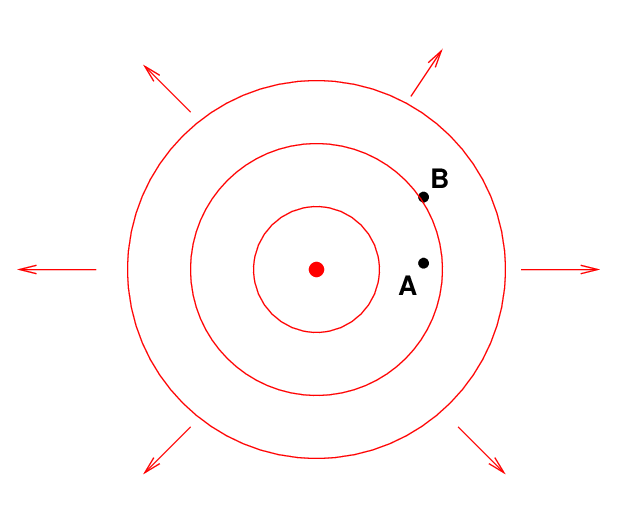
If we move our sensor just a little in a direction perpendicular to the line of sight, again from A to B in the diagram below, the intensity of the waves also changes -- though by a smaller amount.
We call this region close to the source the "spherical wave regime", and the waves themselves spherical waves, for obvious reasons.
But if we follow the waves outward to larger and larger distances, we will find that some properties of the waves appear to change.
Far, far away from the source, the wavefronts appear nearly flat, rather than curved.
If, at this large distance, we move our sensor just a little closer to or a little farther from the bulb, the intensity of the waves changes barely at all; we can approximate it as being constant.
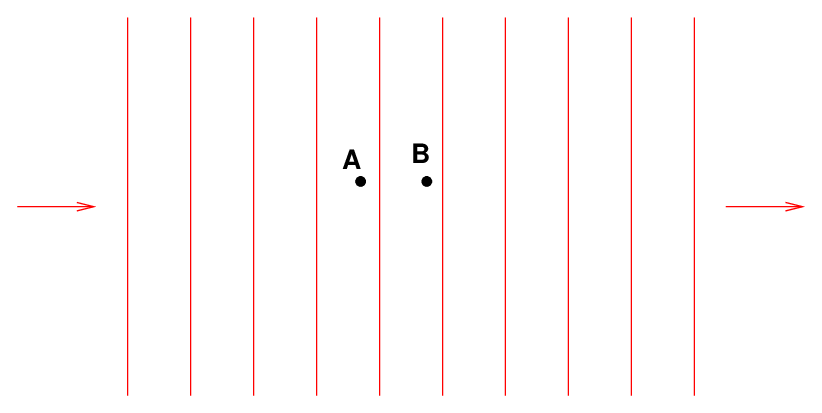
If we move our sensor just a little in a direction perpendicular to the line of sight, the intensity of the waves again barely changes; it is even more nearly constant.
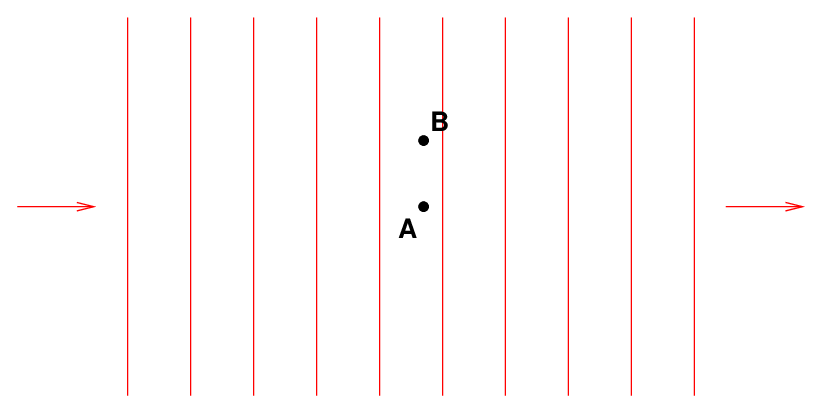
We call this region far, far away from the source the "plane wave regime", and the waves themselves plane waves.
As you might imagine, analyzing the properties of waves is much, much more simple in the plane wave regime.
The Dutch physicist and astronomer Christiaan Huygens came up with an idea around 1690 which, in a way, allows us to connect these two ways of representing waves. His idea was modified and improved by scientists in later centuries; among them was Augustin-Jean Fresnel.
The idea is simple:
any point along a wavefront can act as a new source of spherical waves, each of which has the same frequency and amplitude as its parent
What does that mean? How can we apply this idea?
Consider one wavefront of a plane wave, very far from its source, moving to the right at a speed v.
As time Δt passes, this wavefront moves to the right. A very simple way to imagine this happening is ... just to move the wavefront to the right by an amount v (Δt). Simple, easy. Perfectly adequate in most situations.
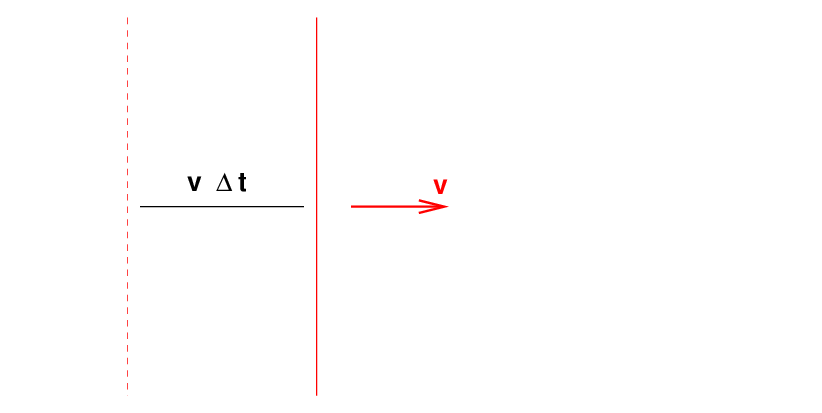
But we can also imagine the process of motion in a different manner. Using Huygens' idea, we can imagine many points along the linear wavefront which each produce a spherical(*) wave. (Click to activate)
(*) well, hemi-spherical. One of the changes made to Huygens' original model is to make the amplitude of these mini-waves dependent on the angle relative to the original source. My hemi-spheres are very rough approximations to the real models.
The spherical mini-waves expand outward and overlap. The overlapping waves produce a new wavefront, which has the same size and speed as the original one -- but which moves away from the source.
This seems like a more complicated way to conceive of wave motion. And it IS more complicated to handle numerically; after all, it assumes that there are an infinite number of little sources of spherical waves. Such a pain in the neck ... why bother with this crazy idea?
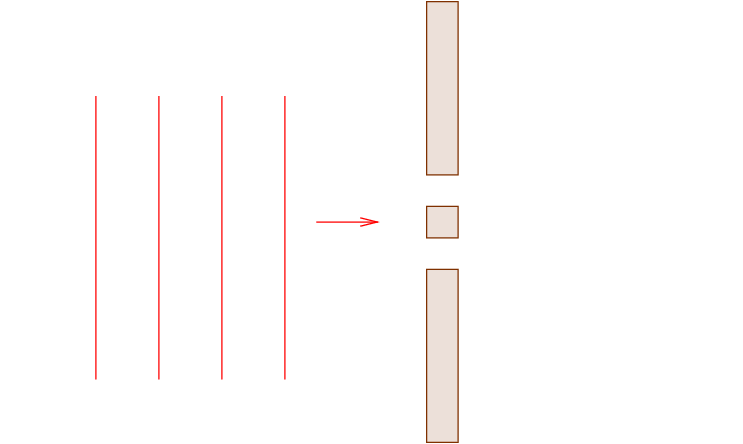
The answer is that in SOME circumstances, Huygens' Principle helps us to understand what will happen. For example, consider a plane wave as it approaches a little hole in a solid wall.
Q: What will happen when the wavefront reaches the wall?
a) it will be completely reflected
b) a small portion will go through hole and continue in straight line
c) a small portion will go through hole and create spherical wavefront
(Click on the figure to find out)
What happens is that a small section of the plane wave does go through the hole; but when it comes out the other side, the plane wave turns into a spherical wavefront.
The nice folk at MIT set up a tank of water to illustrate this phenomenon. Click on the picture below to watch a video.
Image and video courtesy of
Technical Services Group at MIT
(see also local copy)
Q: What will happen if we make two holes in the wall?
Go to 2:00 in the MIT video to find out. You can compare the behavior of real waves in the ripple tank to a calculation of the interference pattern in our next lecture.
Another situation in which Huygens idea can come to our aid is the when a wave strikes a boundary between two media at some angle which is not perpendicular to the boundary.
To illustrate the action, I will draw upon a most excellent applet:
Suppose that a wavefront travelling through a medium with an index of refraction n1 = 1 approaches a region with a larger index of refraction, n2 = 2.
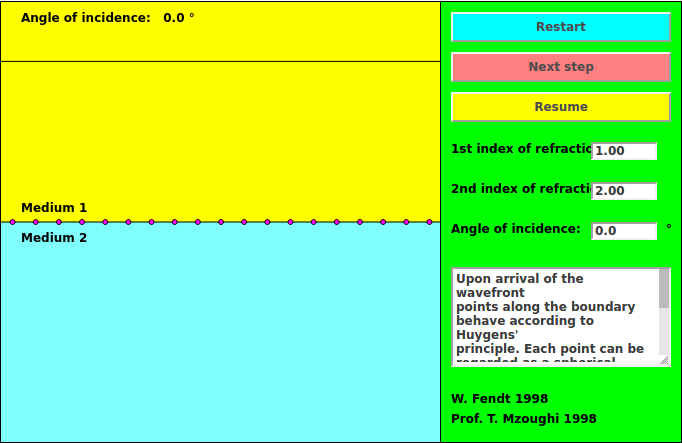
Q: How does the speed of the wave change when it enters region 2? Q: What effect will that have on the direction of the wave?
Because the wave travels more slowly in region 2 (by a factor of n2 / n1 = 2, in this case), the distance by which each mini-wave penetrates into its medium is smaller in region 2 than in region 1. There are two obvious consequences:
Pretty simple, right?
Well, let's look at a slightly different situation. Suppose that the incoming wave front approaches the interface at an angle.
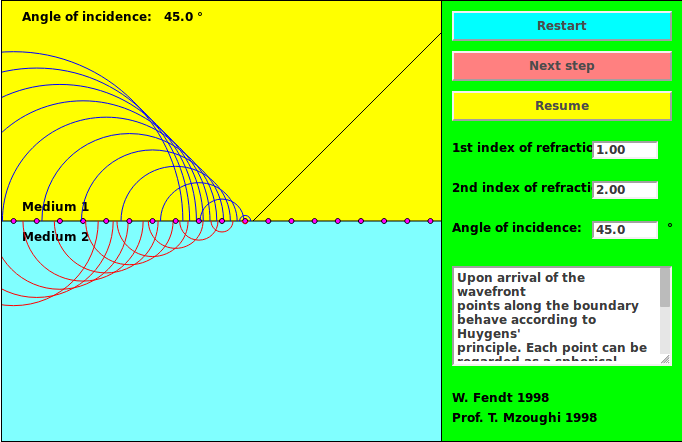
Q: How does the speed of the wave change when it enters region 2? Q: What effect will that have on the direction of the wave?
Once again, the wave travels more slowly in region 2; but this time, that causes the wave front in the transmitted region to leave the interface at an angle which is NOT THE SAME as the angle of the reflected wave (or the incident wave). Just what is that angle?
To find out, let's draw some triangles based on:
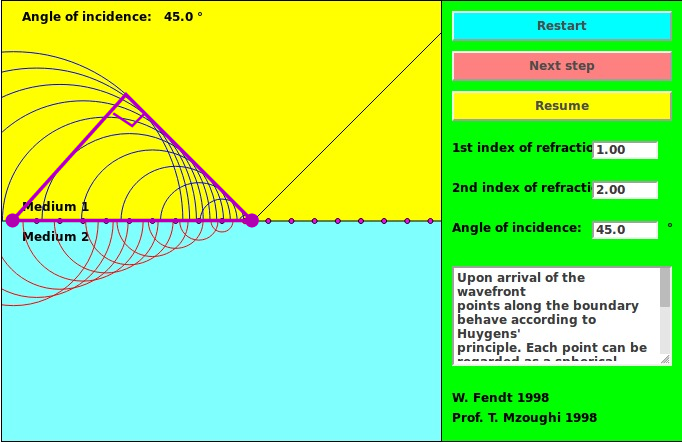
... but a smaller triangle in region 2, because the wave propagates more slowly through medium 2.
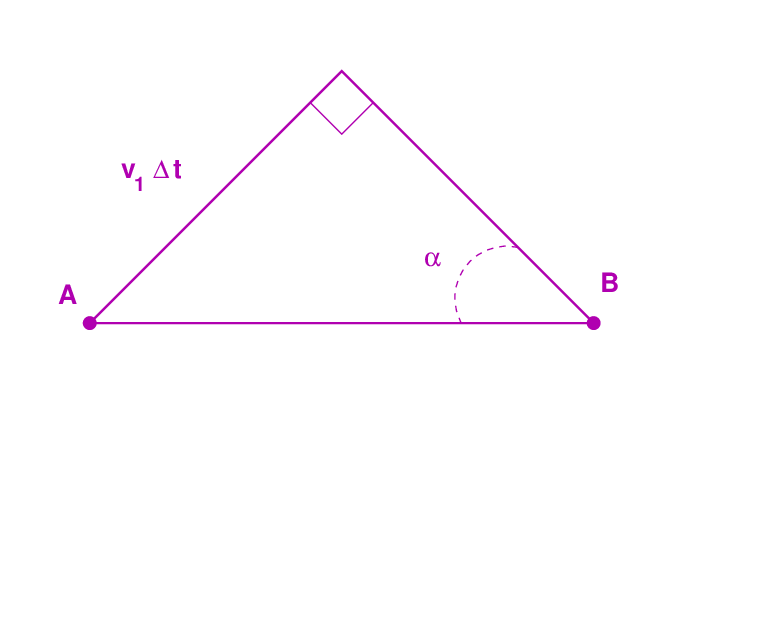
Note that the two triangles share one common side, AB, which is the hypotenuse of each one. This side, AB, is the distance along the boundary defined by the point of contact between wavefront and boundary at two particular times, tA and tB. We can define a time interval Δt = tB - tA.
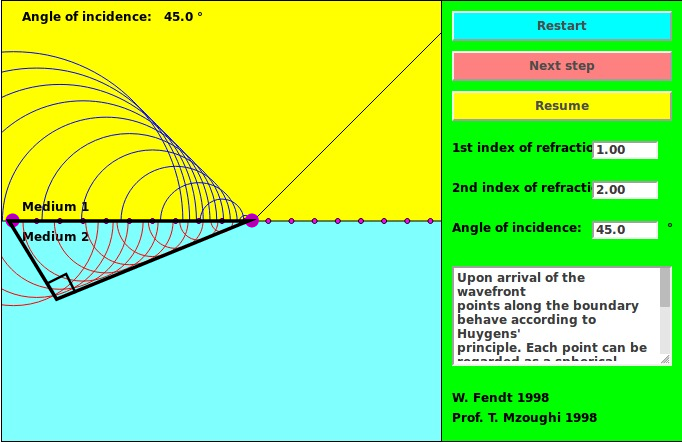
If we zoom in on the triangle in region 1, we can see that the side which runs from point A upwards has a length which is equal to the distance the wave can travel in the time Δt.
The triangle in region 2 has a shorter side projecting into medium 2, because the waves travel more slowly and so cover a smaller distance in the time Δt.
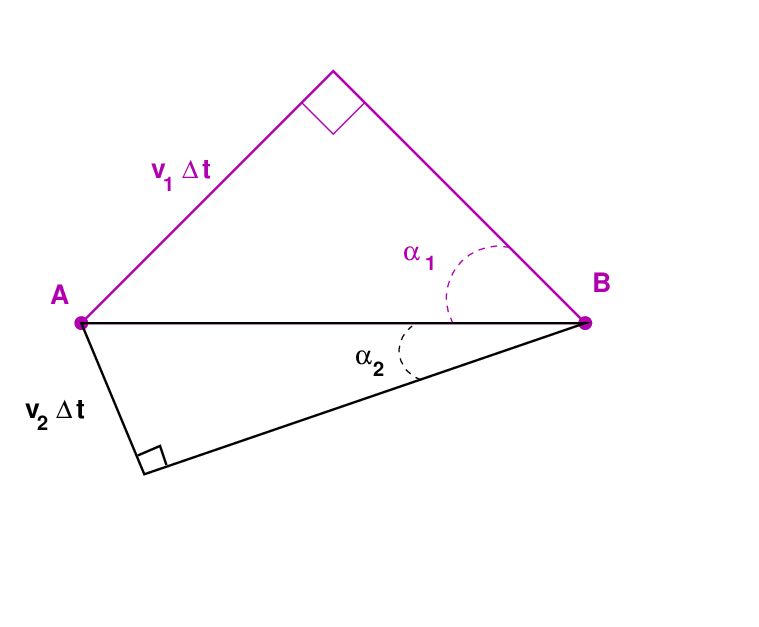
Q: Can you find a relationship between the angles labelled
α1 and α2, and the indices of refraction n1 and n2?
Perhaps these hints might help.
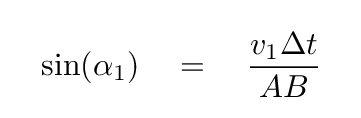
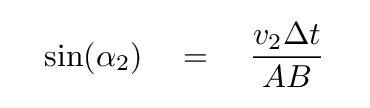
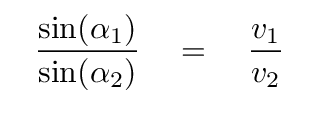
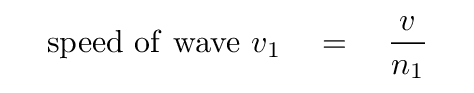
Does this look familiar?
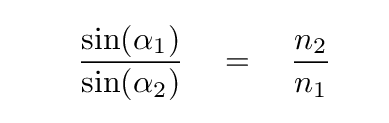
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.