
Image from afarTV
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

Image from
afarTV
See also another lightning/thunder video.
Today's topic is how fast do waves travel? In particular, I want to find out do all waves of a certain type travel with the same speed? For example, light waves: you probably know that all electromagnetic waves -- such as optical, radio, or ultraviolet -- travel at the same speed in a vacuum: good old c = 299,792,458 m/s.
But is that true if the waves travel through air? Or glass? Or ionized gas in space?
In order to answer that question, we'll going to go back to the basics. Remember that the speed of a wave depends on its wavelength and frequency:
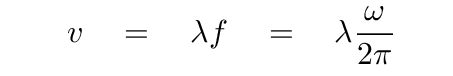
Let's first look at the special case of waves travelling along a string to see how the wavelength and frequency of waves might vary, and what that might mean for the speed of the wave. We'll then move on to consider other types of waves.
Last time, we determined that the vertical position of section p of a string stretched between two fixed posts, vibrating in its normal modes, would be given by
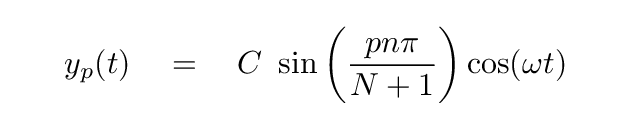
The middle section of this equation, the sine term, describes the shape of the string at any moment in time. There are a number of solutions, which one can describe by the index n of the normal mode. The first few shapes look like this:
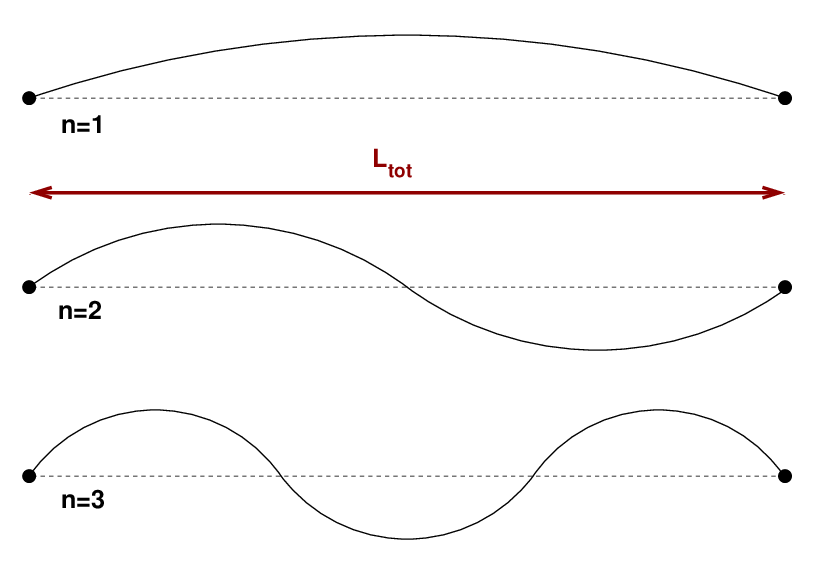
Note that the index n is equal to the number of anti-nodes in the string.
The total length of the string is the number of segments, N, times the length of each segment, L.
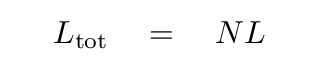
We can describe the wavelength of the motions of the string in terms of this total length of the string.
Q: Do you remember a formula which gives the wavelength
of the first few normal modes?
By looking at the pictures, one can easily verify that
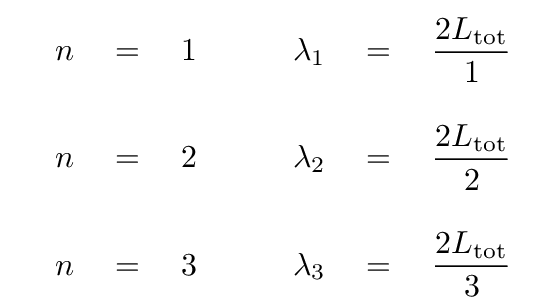
In general, the wavelength of the n'th mode is
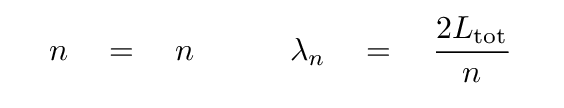
Another property of these normal modes is their frequency. We derived a simple formula for the frequency of mode n last time:
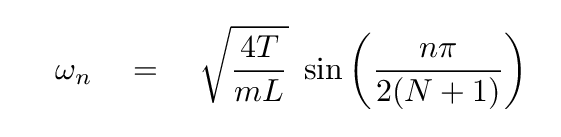
When we make a good approximation to a real, continuous piece of string, we must use many, many sections; in other words, a very large value of N: thousands, or millions, of sections. In other words,
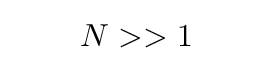
If we focus on the first few normal modes, say, n = 1, 2, 3, then
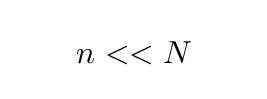
Clearly, then, for these first few modes,
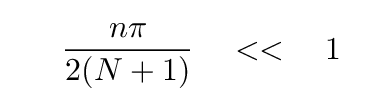
The sine of a small quantity is approximately equal to that small quantity itself, so
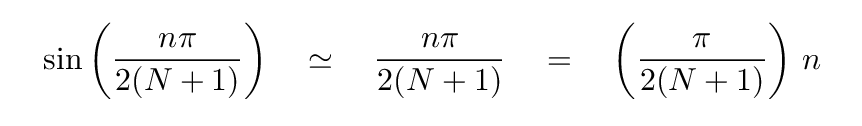
And so the frequency of the normal mode n grows linearly with n ...
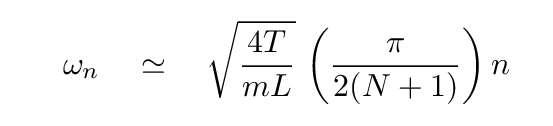
... at least at first.
We haven't quite yet reached "waves" in this course, but I'm going to jump ahead a bit to discuss one aspect of them; it's a good time to do so, based on the derivation of the frequency of normal modes we just finished.
You should recall from your first-year physics course that the speed of a wave depends on its frequency and its wavelength:
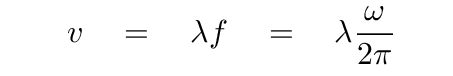
So, if we just plug in our expressions for the wavelength and frequency of the normal mode n, we find a speed of
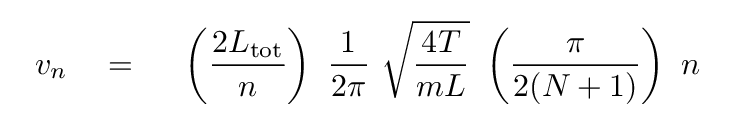
Q: How does this speed change with the mode index n?
The answer is -- it doesn't! The speed of a wave on a string is constant, the same for all modes. How convenient!
But -- wait a minute. Is it really constant? The wavelength DEFINITELY decreases linearly with n; no question there. For small values of n, yes, the frequency grows linearly with n. So, for low frequencies, the speed should be constant.
But what happens at high frequencies? What happens, for example, when
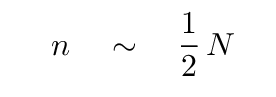
At these large mode index values, the argument of the sine function is NOT small, and so the value of the sine function is NOT approximately equal to its argument.
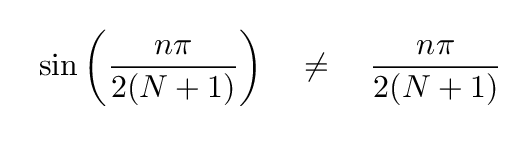
Q: How does the sine function grow for these modes?
a) faster than n
b) slower than n
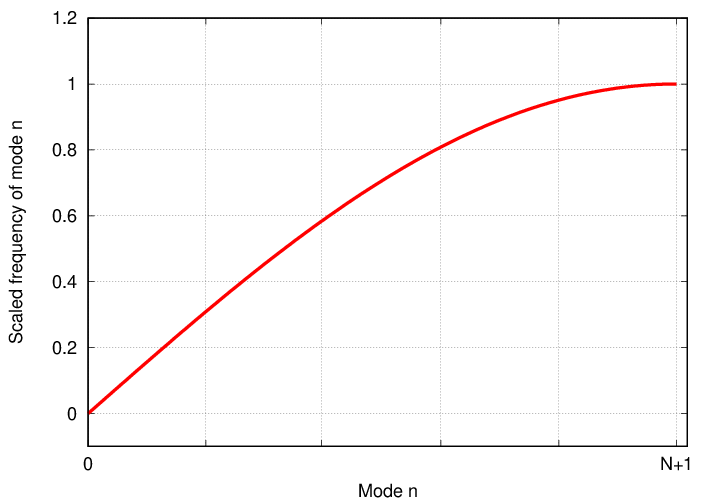
For small mode indices, the frequency does grow linearly with n; but for large mode indices, the frequency grows MORE SLOWLY than n.
So what? Well, that means that for waves travelling on a string,
In other words, the speed of waves on a string does change with frequency. We call this phenomenon dispersion.
Not all waves suffer from dispersion. It all depends on the physical nature of the wave in question. For example,
Well, strictly speaking, the speed does vary SLIGHTLY -- but by very very small amounts. The graph below shows data based on the measurements listed in L. B. Evans and H. E. Bass, "Tables of absorption and velocity of sound in still air at 68F (20 C)", Technical Report No. AD0738576, Wyle Labs, Huntsville, AL, (1972-01-01), as found at https://apps.dtic.mil/sti/citations/AD0738576 . Click to see the ugly truth
Q: If the audience at a music concert sits d = 40 m away from the stage, how large a time delay occurs between notes at f1 = 100 Hz and f2 = 1000 Hz? Would the audience notice?
Let's take a closer look at that last example. A "plasma" is simply a gas in which some of the atoms are ionized. There's a lot of plasma in outer space. The huge voids between the stars in our Milky Way Galaxy, and the even larger abysses of emptiness between galaxies, a filled with very, very, very thin clouds of gas. Most of this gas is hydrogen, and small amounts of it are ionized by high-energy photons emitted by hot stars and energetic events in the centers of galaxies.
When electromagnetic waves pass through a plasma, they interact with the charged particles in a particular manner. It is convenient to compute a quantity called the plasma frequency, which depends upon the density of the gas.
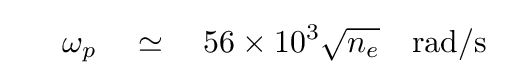
In this equation, the quantity ne stands for the density of electrons per cubic centimeter. A typical value for average clouds in the Milky Way is something like ne = 0.03 .
It turns out that the speed (group velocity, for those of you who have read ahead) of radio waves of angular frequency ω travelling through a plasma can be calculated as
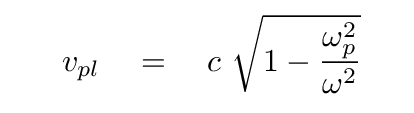
If we adopt an average electron density of ne = 0.03 per cubic centimeter, then we can simplify this to
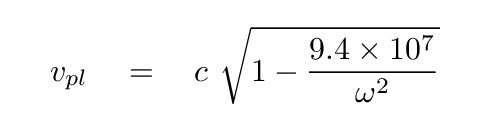
How different is this speed from c, the ordinary speed of light? Well, let's see. Suppose we look at a frequency of f = 300 MHz, which corresponds to an angular frequency of ω = 1.89 x 109 rad/s.
Q: What is the speed of these radio waves through space? Q: How different is it from the speed of light through a vacuum?
Now, that LOOKS like a very small difference, and it IS a very small difference ... but when light has to travel interstellar distances, it can really add up.
Suppose that we observe a pulsar at a distance of D = 6500 light years. The time for light waves to reach us through a vacuum would be
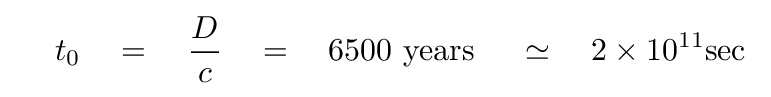
But if we observe light which has passed through a typical instellar medium, with a typical electron density, then it will take a bit longer. The extra time will depend on the frequency of the light. Let's work out the numbers for two different radio frequencies.
300 MHz = 1.89 x 109 rad/s 400 MHz = 2.51 x 109 rad/s
---------------------------------------------------------------------------------------
v = v =
t = t =
t - t0 = t - t0 =
---------------------------------------------------------------------------------------
Suppose that one can measure the dispersion of waves coming from some celestial source. If one has a rough idea of the average density of electrons in the interstellar medium, one can use the amount of dispersion to estimate the distance to the object. This is sometimes the only way to guess how far away some mysterious object might be.
For example, in the past few years, radio astronomers have discovered a number of Fast Radio Bursts (FRBs). These are exactly what the name describes: very brief bursts of radio waves, lasting much less than a second. We have found only 40 or 50 of them, and in most cases, they appear just once, and never again, from a particular region of the sky. Are they exploding stars, or merging neutron stars, or the result of new physics? We just can't tell. Very frustrating!
In 2017, astronomers caught a break. One particular source, known as FRB 121102, has been observed a number of times over the years. Whatever creates this burst (and all bursts? We don't know) apparently doesn't destroy the source. After months of listening, one radio telescope observed a bright burst from this source, and was able to pin down its position precisely. Below is a picture showing the radio sources in the region of sky around the source, with an inset showing an optical picture.
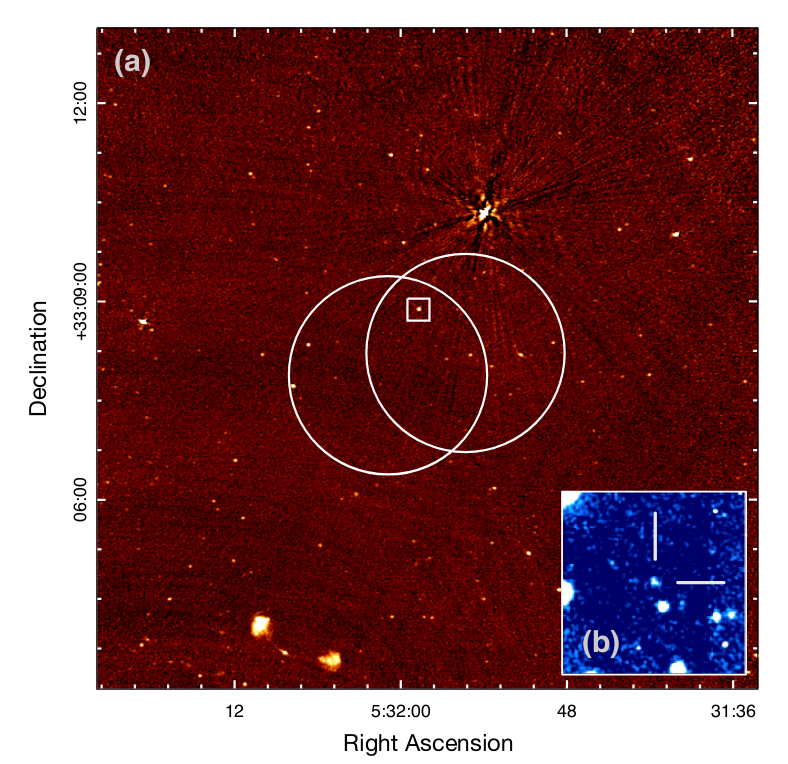
Taken from Figure 2 of
Chatterjee et al., Nature 541, 58 (2017)
You can see a large number of faint radio sources in this general area; until this particular burst was observed, astronomers didn't know which of these faint sources corresponded to the FRB.

Figure 7 taken from
Chatterjee, AstroBeat, March 2019
The optical image, above, shows a small, faint, blurry object at the position of the radio source. Could this be a nebulosity in own Milky Way Galaxy? Or was it a very distant galaxy, far, far outside the Milky Way?
Well, the radio astronomers observed the burst at a range of different frequencies, and this provided a key to solving the mystery. Look: the high-frequency radio waves arrive a fraction of a second before the low-frequency waves.
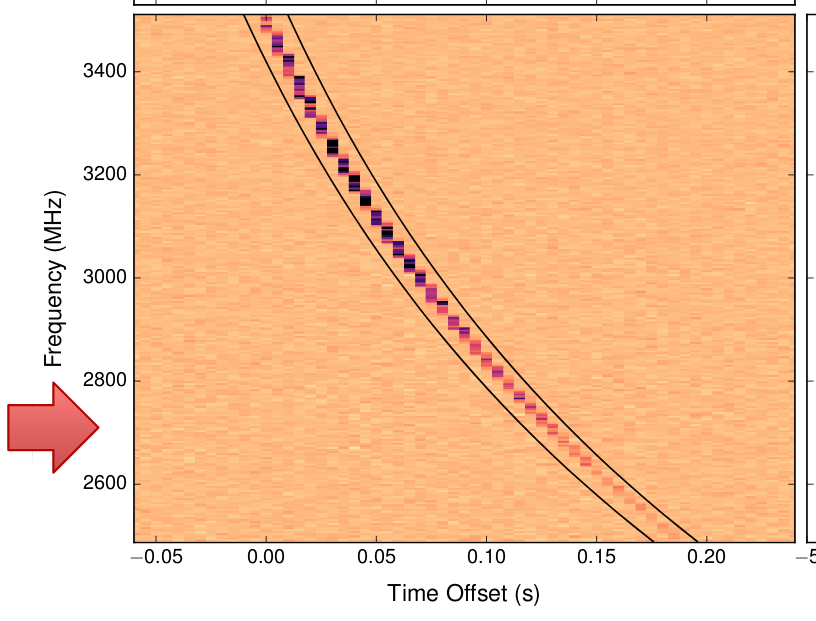
Taken from Figure 1 of
Chatterjee et al., Nature 541, 58 (2017)
The difference in arrival time between waves of two frequencies will allow us to estimate the distance to this object. First, compute the speed of radio waves through typical interstellar plasma at these two frequencies. Express each speed as c multiplied by (1 - something).
3400 MHz = 21.36 x 109 rad/s 2600 MHz = 16.34 x 109 rad/s
---------------------------------------------------------------------------------------
v = c * (1 - ) v = c * (1 - )
---------------------------------------------------------------------------------------
The time it takes for the waves to reach us will simply be the unknown distance D divided by these speeds.
3400 MHz = 21.36 x 109 rad/s 2600 MHz = 16.34 x 109 rad/s
---------------------------------------------------------------------------------------
D D
t1 = --------------------- t2 = --------------------
c * (1 - ) c * (1 - )
D D
= ---- * ( 1 + ) = ---- * ( 1 + )
c c
---------------------------------------------------------------------------------------
And therefore the DIFFERENCE in arrival time can be expressed as
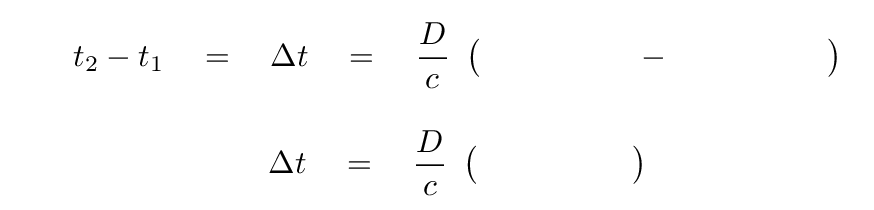
Inverting this equation allows us to compute the distance to the source.
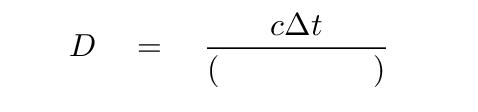
Q: What distance did you compute to this source?
Q: The Milky Way, in this direction, extends about 15,000 light
years or so. Is this source inside or outside
the Milky Way?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.