
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Today's lecture is brought to you by

This time, we look at the interaction of light with a SINGLE slit in a wall, and on its subsequent journey to a distant screen. The big difference between our examination of the situation, and the one you saw in University Physics, is that we will not only ask "where are the bright and dark spots?", but also "what is the intensity in between the spots?"
Waves travel from left to right toward a wall, which has ONE small slit, of width a. On the other side of the wall is a large empty space; only after travelling a distance L will any waves reach a second wall.

Again, we require that the waves approaching the left-hand wall be coherent: they must all have the same wavelength and present the same phase all the way across the single slit. One way to make this happen is to place a single source of waves far, far to the left of this wall, so that it lies in the plane wave regime of that source.
The big question is: what happens to any waves which travel through the slit?
(spoiler)

Our approach today will be to apply Huygens' Principle to the situation. The slit in the first wall will contain a large number of sources of a new set of waves.

Each of these sources emits in a spherically symmetric way (well, at least hemi-spherically), so we can write the equations of waves emitted by each source as
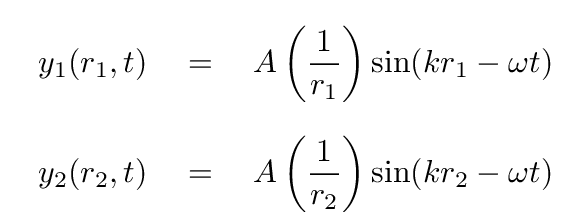
where the subscripts refer to two of the mini-sources.
What happens if waves from two of the mini-sources happen to meet? They simply add together, of course.
We will again restrict our results to the far-field region -- on the right-hand screen, for example. In this region, one approximation we can make safely is that the magnitude of ANY of the radial distances -- r1 and r2, and so forth -- is nearly the same, so we use an average radial distance to divide the amplitude of the sum.
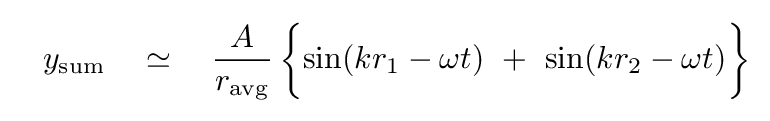
(If you want to know where the maxima of the pattern are located, you'll need to wait until the end of this lecture. That's a much more difficult question to answer)
Let's begin with a simple question: when waves from all the mini-sources in the slit interfere on the distant screen, are there any locations at which the sum is ZERO? There were for the two-slit experiment -- how about this one-slit experiment?
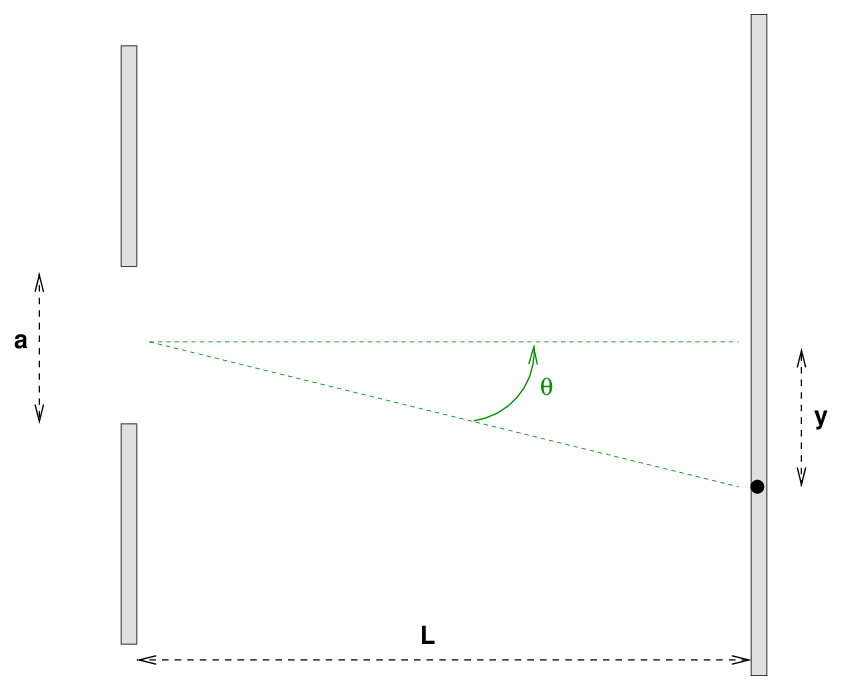
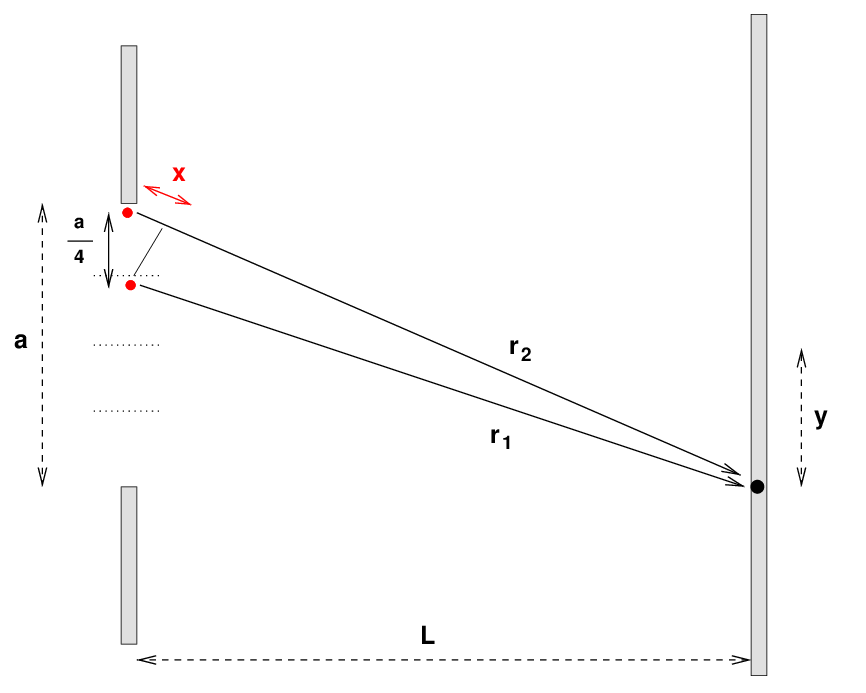
We'll begin just as we did in our our discussion of two-slit interference, by considering some point on the distant screen which is an angle θ from the center of the screen; or, equivalently, a distance y away from the center.
One quick and easy way to find the locations where the interference is purely destructive is with a clever trick: break the slit into two halves, and create pairs out of one mini-source from each half. We begin with a mini-source just below the top of the slit, and match it with a mini-source just below the half-way point.
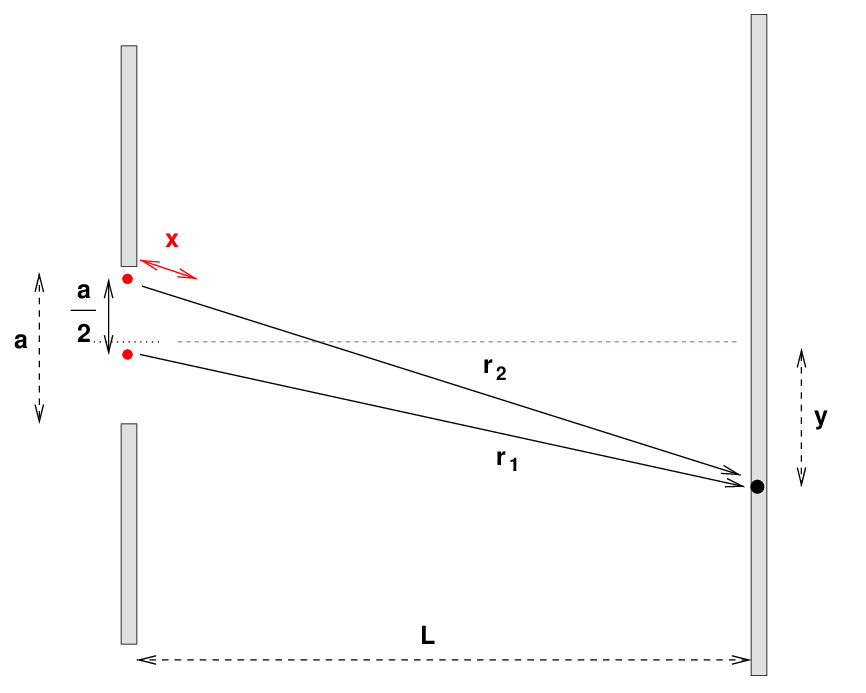
If the separation of the mini-sources a/2 is much smaller than the distance between the walls L, then the two radial vectors are NEARLY parallel. In that case, the extra distance x travelled by the upper wave can be approximated very well as
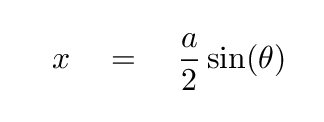
If we wish to locate the first location where the sum of the two waves is zero, we require that extra distance to be exactly one half-wavelength.
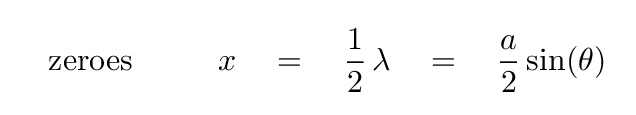
Q: Can you write an equation for the angle θ
which will yield zero net amplitude?
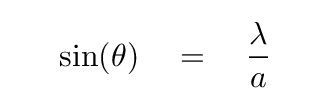
Q: Can you write an equation for the location of this zero spot
on the distant screen? How far y will it be
from the center of the screen?
And therefore the first zero will appear a distance away from the center of the distant screen

(We'll need to remember this relationship between the angle θ and the location on the wall y later, so I'm putting it inside a green box)
We can follow a similar procedure to find the location of the second zero. This time, we split the slit into 4 equal sections, and create pairs of mini-sources which are a distance a/4 apart.
Now, the extra distance travelled is
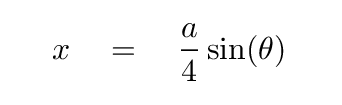
and so we find
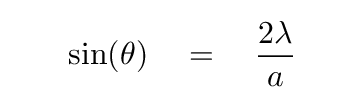
which leads to the position of the second zero,
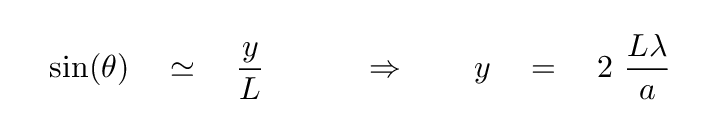
We can break up the single slit into more and more equal sections, each time arranging the mini-sources in pairs, to derive the general relationship for the positions of zeroes on the distant screen:

Finding the positions at which the waves interfere in a completely destructive manner is relatively easy. But what about the locations between these zeroes? What is the sum -- and the intensity -- of the waves at those positions?
This is a more complex problem. There are both algebraic and geometric approaches to solving it. I'll try using some algebra and a little calculus to do the job here.
Let's make one small addition to our diagram: we will introduce a variable, z, which measures the distance vertically above the bottom of the slit. So, if we move from the bottom of the slit to the top of the slit, the variable z will increase from zero to a.
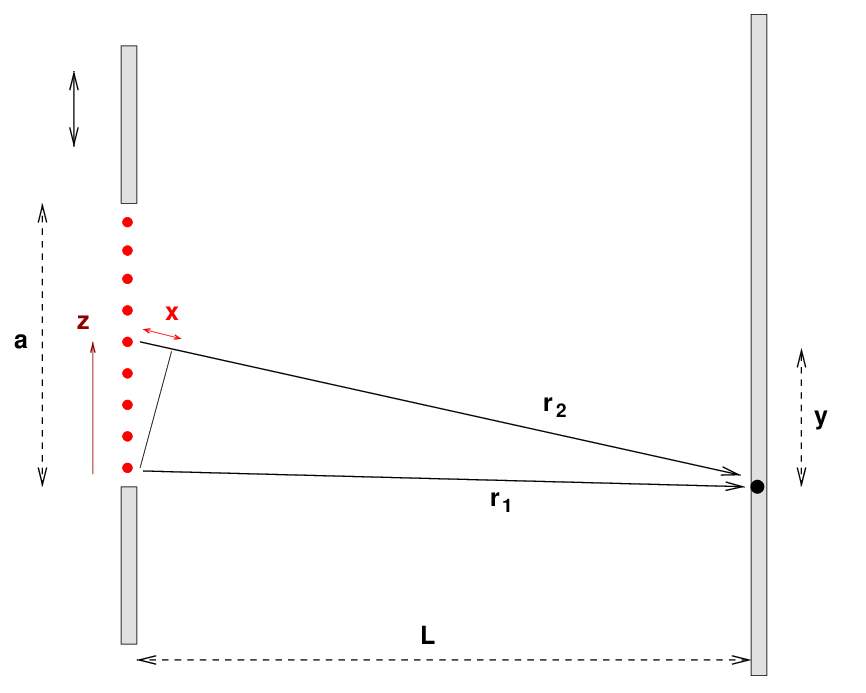
We will try to compute the amplitude and intensity of the waves which strike a point P on the distant screen, at some angle θ, or linear distance y, from the center of the screen.
Let's divide the single slit into many, many tiny sections, each of which is dz wide. There is a Huygens mini-source at the boundary of each section. The figure below is zoomed in to show a closeup of the waves leaving two adjacent mini-sources.

The extra distance travelled by one wave, compared to that of its neighbor, is
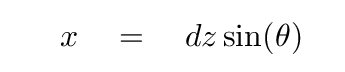
We can express this extra distance in terms of the number of wavelengths travelled
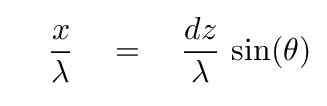
or in terms of radians.
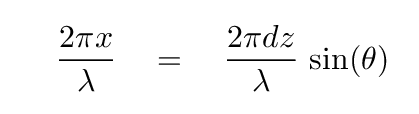
If we consider not just an adjacent mini-source, but some mini-source at an arbitrary vertical distance z from another in the slit, the phase difference between their waves will be
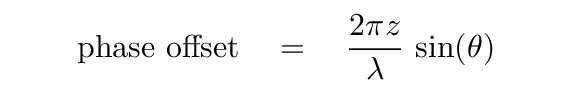
Suppose that the incoming wave which enters the slit has an amplitude A. The sum of the waves produced by all the little Huygens mini-sources must add up to this same amplitude. If we break the slit up into 2 pieces, the amplitude of each mini-wave must be A/2; if we break it up into 10 pieces, the amplitude of each must be A/10. But if we break it up into a/dz pieces, the amplitude of each must be
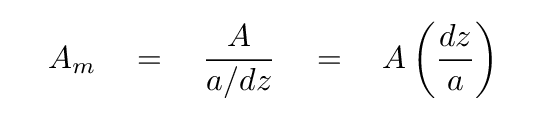
(I'm putting a solid red box around this equation because we'll need to use it a bit later. Don't forget it)
So, we can write an equation for the wave emitted by any particular mini-source within the slit in the following way: for mini-sources 1 and 2, we have
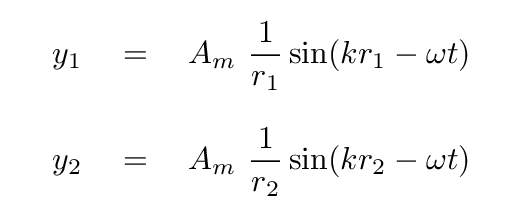
and so forth and so on.
As long as the slit is very small compared to the distance between wall and screen, a ≪ L, we can approximate the radial 1/r term as equal for all these waves. In that case, we can simplify to
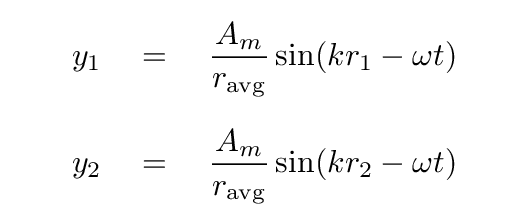
But even the slight differences in the radial distances r1 and r2 can't be ignored INSIDE the sine function; those small differences will lead to offsets in phase between the waves when they arrive.
Here comes a tricky bit. Once we've chosen a particular location P on the distant screen, we know exactly how much farther each mini-source's wave needs to travel, compared to its neighbor. That extra distance means that each mini-wave will arrive a little later, in phase, when it meets its neighbor. That phase offset will be
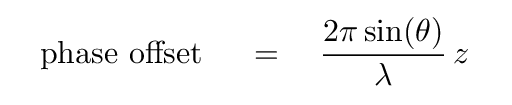
Let's compare the first mini-source at the bottom of the slit to the mini-source located a distance z away from it,

We can re-write the equations of the waves which strike the point P from these two mini-sources using this offset in phase, rather than the radial distance:


If we want to add together the waves emitted by ALL the mini-sources, then we need to integrate:
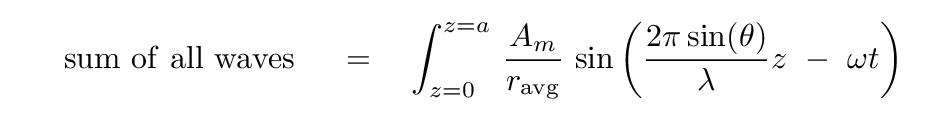
What a minute, that integral looks ... not quite right.
It seems almost, well, naked. As if it were missing
something to cover up its right-hand end ....
Q: What is missing from this integral?
It needs a differential quantity. If we're integrating over all distances z, then we need a dz. And I know just where to find one!
At this point, let's replace the amplitude of each mini-wave with its equivalent expression in terms of the amplitude of the original wave -- remember that red box?
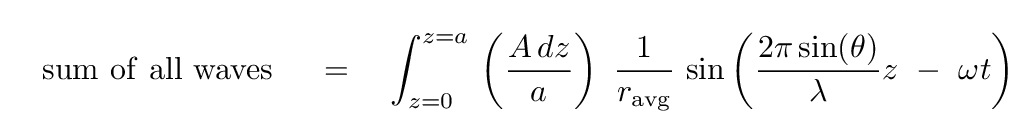
Note that we now have a proper integral, once we put the dz inside.
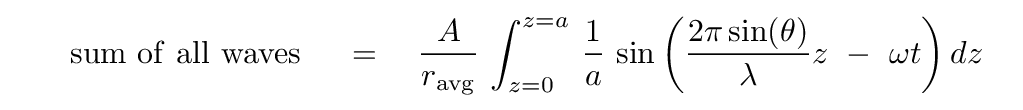
So, let's integrate!
Q: Is this a really difficult integral?
Not difficult, no. Just a bit messy, with all those variables here and there.
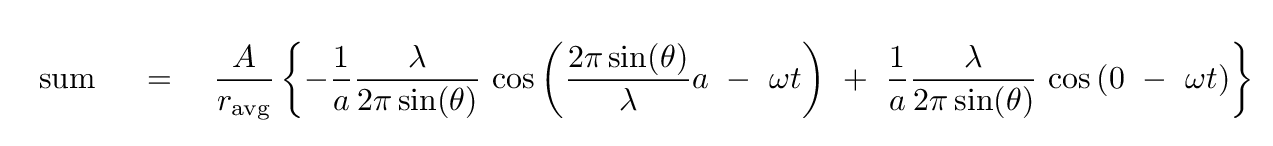
Ugh. That's one long and unwieldy expression. We can shorten it a bit by introducing a new variable

That makes our integral look like
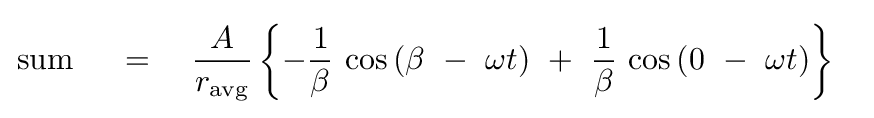
Aha. This is the difference of two cosines. We can apply a trig identity,
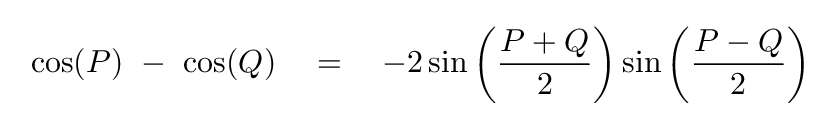
in which we substitute P = -ωt and Q = β - ωt, which will turn the integral into
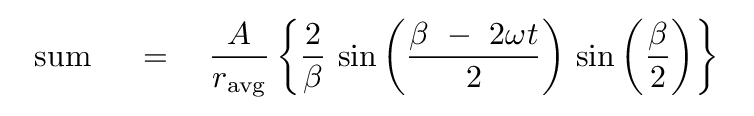
The intensity of a wave depends on the SQUARE of its amplitude, so at the point P of the screen, the net intensity at any time t is
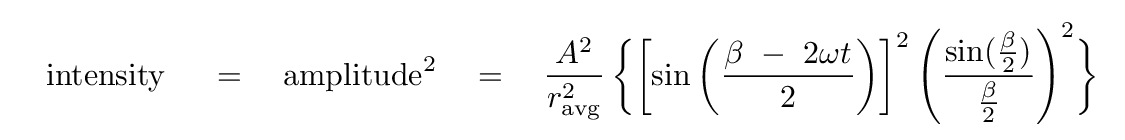
The first of the sine terms inside the brackets depends on time; the second one does not. If we integrate over a long time, we can pull everything but that first sine term out of the integral, and find that the integral of the sine-squared term yields 1/2. So, we end up with a time-averaged intensity of

Do you recognize that function inside parentheses? That combination of sin(x)/x is called the sinc function.
Recall that the variable β in this equation contains sin(θ). it tells us how the intensity changes as we move in angle away from the center of the distant screen.
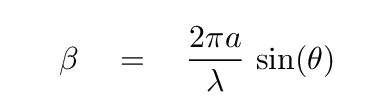
We can also express that as a function of the linear distance y away from the center of the screen (remember the green box?)

Values of the intensity as a function of distance for a typical classroom setup are shown below. Note that the intensity of the first maximum is very small compared to that of the center: only about 5 percent.

You can see the same thing in a real-life diffraction pattern made in one of our optics labs:
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.