Cephids and the Distance to the LMC

By comparing the color-magnitude diagrams for clusters of stars in our Milky Way Galaxy, we can calculate their relative distances. Hipparcos observations of a few very close clusters (such as the Hyades or Pleiades) allows us to turn these relative distances into absolute ones. But we can't measure the brightness of main-sequence stars in other galaxies very accurately -- they are just too far away and therefore too faint. How can we determine the distances to other galaxies?

There are a number of different methods, but the main technique depends on the properties of a particular class of stars, called Cepheid variables.

Cepheids are great relative distance indicators, but we need to know how just how luminous they are in order to calculate absolute distances. For better or for worse, astronomers have decided to base all their Cepheid distances on a single galaxy: the Large Magellanic Cloud, or LMC.

What are Cepheids?

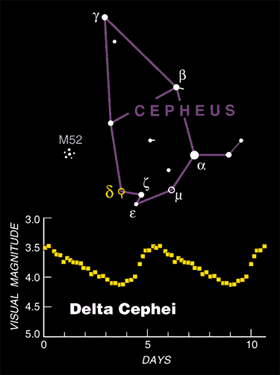
The star delta Cephei varies by about 50% in brightness over a period of about 5 days:

Graphic from Sky and Telescope's website http://skyandtelescope.com/observing/objects/variablestars/article_160_1.asp

There are many other stars which vary in a similar way, showing a smooth light curve which often features a quick rise and slow fall. For example, the star eta Aquilae:

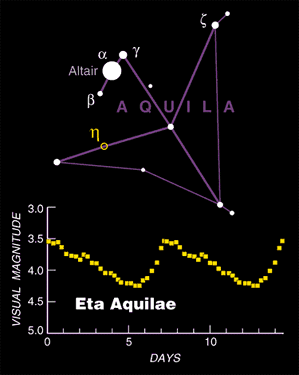
Graphic from Sky and Telescope's website http://skyandtelescope.com/observing/objects/variablestars/article_160_1.asp

When one measures the radial velocity of Cepheids, one finds a cyclic variation, which has the same period as their change in brightness.

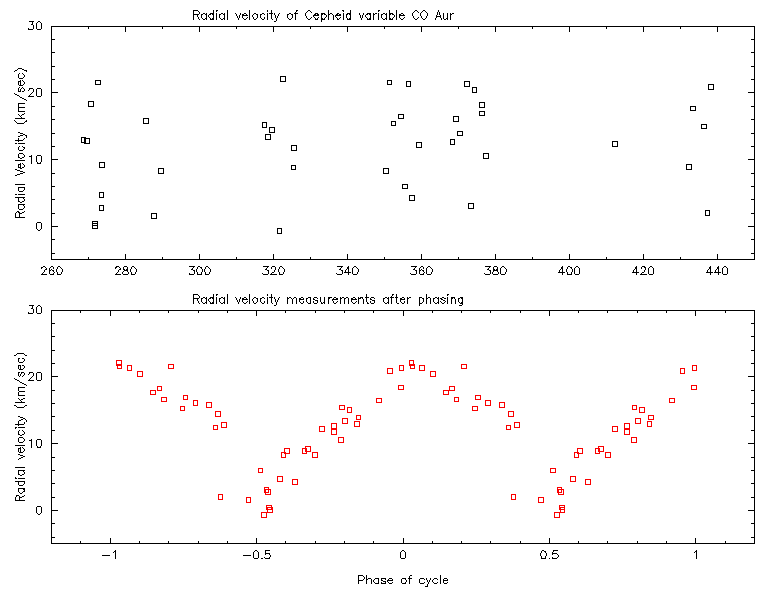
It turns out that Cepheids are pulsating variables: their outer atmospheres puff outwards, making them larger and brighter, then cool off and fall back, making them fainter.

Some of the stars have short periods of a few days; others take weeks to complete one cycle in brightness. All of them are relatively bright, young stars. They appear in the color-magnitude diagram in an area like this:

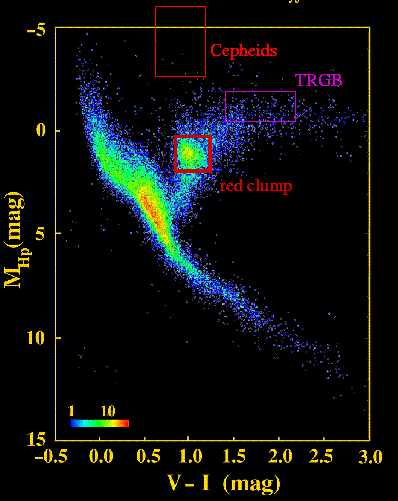
As the figure shows, these stars are

very bright, which means that we can see them even in other galaxies, but
very rare, so rare that very few are close enough to the Sun to have parallaxes large enough for Hipparcos to measure

Some astronomers have tried to combine marginal measurements of many Cepheids to derive an "average" parallax, but most astronomers don't give that much weight.

So, how are these stars going to help us to measure distances?

Henrietta Leavitt's discovery of the period-luminosity relationship

In the early 1900s, the Harvard College Observatory was one of the leading astronomical research institutions in the world. It employed many men to build equipment and go observing, many women to examine and measure photographs and perform numerical computations, and a few lucky male astronomers to analyze the results and publish them.

One of the women, Henrietta Leavitt, was given the task of examining photographic plates of stars in the Small Magellanic Cloud (SMC), one of the little satellite galaxies which orbits our Milky Way. She used a clever technique to find variable stars: given two photographs from different dates (both of which were negatives, showing black stars on a white background),

she would make a positive copy of one

and lay it over the negative original of the other. Stars which had the same brightness on both plates would very nearly cancel each other out, leaving a plain grey; but stars which varied from one plate to the other would leave bright or dark rings.

After several years of work, Miss Leavitt (for that was the form of address in those days) found 1,777 variables in photographs of the SMC and LMC. A small fraction of these were Cepheids. She noticed that the Cepheids with long periods were brighter than those with short periods, whether she used the magnitude at maximum light or minimum light.

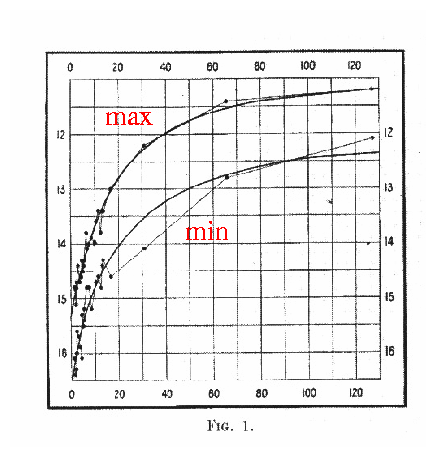
The effect was even more striking when she made a logarithmic plot of both variables (brightness in magnitudes versus logarithm of the period):

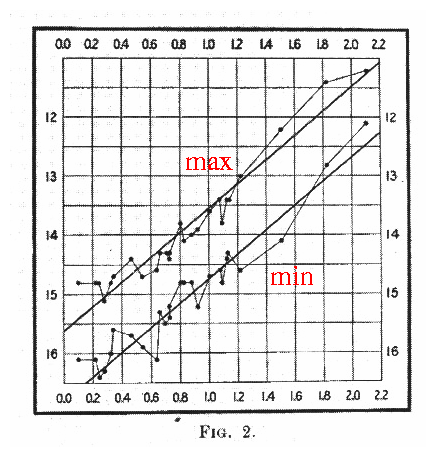
She wrote

The two resulting curves, one for maxima and one for minima, are surprisingly smooth, and of remarkable form. In Figure 2 ... a straight line can readily be drawn among each of the two series of points corresponding to maxima and minima, thus showing that there is a simple relation between the brightness of the variables and their periods ... Since the variables are probably at nearly the same distance from the Earth, their periods are apparently associated with their actual emission of light, as determined by their mass, density, and surface brightness.

(emphasis added)

Her results, including these words, were published by Edward C. Pickering, one of the lucky male astronomers who took a great deal of the credit for the work done by the entire Harvard College Observatory crew. See Harvard College Observatory Circular, vol 173, p. 1, 1912.

Leavitt's discovery of a period-luminosity relationship in Cepheid stars was a breakthrough. The period of a Cepheid is relatively easy (though tedious) to measure. If we can figure out the luminosity which corresponds to any particular period, we may use the inverse-square law to estimate the distance to the star.

In recent years, advances in detectors and observing techniques has permitted us to measure this period-luminosity relationship with greatly improved accuracy. Here's a 1960s version of the period-luminosity relationship based on photographic measurements of Cepheids in the Magellanic Clouds:

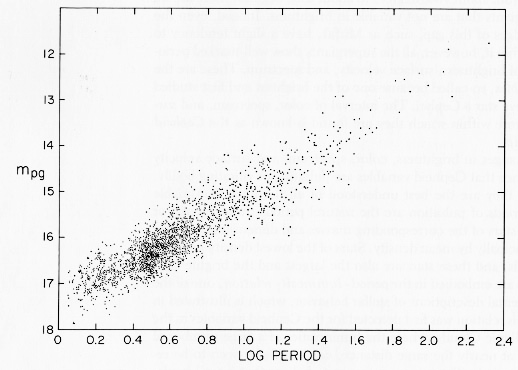
Here's a similar plot, based on data collected by the OGLE collaboration with CCD cameras in the 1990s:

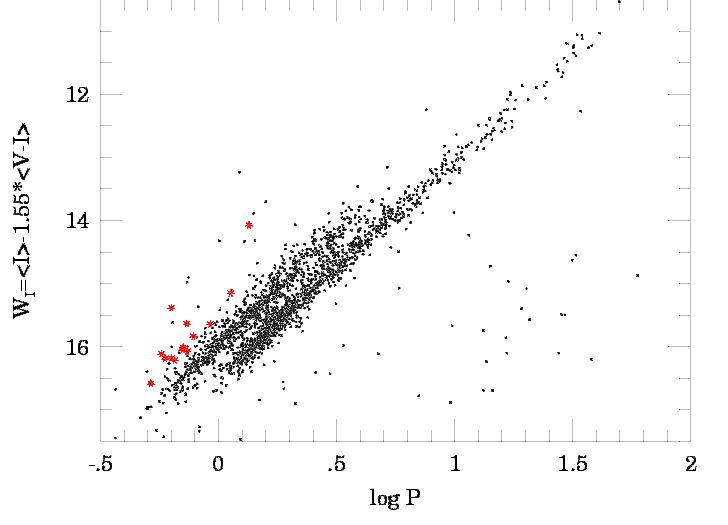
Notice that there are really two tracks in this diagram: the one on the left belongs to Cepheids pulsating in the "first overtone" mode. Back in the old days, we couldn't detect this difference, and so mixed the two sets of stars together -- which added quite a bit of error to distance measurements.

Problem of the "zero-point"

So, it looks as if Cepheids might provide astronomers with an ideal means to measure distances to other galaxies. Just

take a series of pictures,
find a set of Cepheid variable stars,
measure their periods and brightnesses,
make a period-magnitude diagram
compare the diagram to one for the LMC

The amount by which one must slide the diagram vertically (in brightness) to match Cepheids in the other galaxy to Cepheids in the LMC yields the relative distance between the other galaxy and the LMC.

There's just one weak point: how far away is the Large Magellanic Cloud? If we don't know that, we can't convert the relative distances to absolute distances in parsecs. Hmmmm....

If we knew the distances to Cepheid variables in our own Milky Way galaxy, we could compare them to the Cepheids in the LMC, and measure its distance that way. Unfortunately, none of the Cepheids in our own galaxy are close enough for Hipparcos to measure their distances accurately. Rats!

There are a very few Cepheids found within some distant open clusters in the Milky Way. We can use the main-sequence fitting technique to compare those distant open clusters to nearby open clusters, and thereby determine their distances, which in turn give us their Cepheids' distances. Alas, there are so few of these stars in open clusters that this method of calibration still has a relatively high uncertainty.

So, is there any other way -- without using Cepheids -- by which we can determine the distance to the LMC?

The distance to the LMC

Astronomers have tried many different methods to measure the distance to the LMC, since we base upon it all distances to other, more distant, galaxies. Here's an incomplete list of those methods:

RR Lyrae stars are another class of pulsating variable stars. They are much fainter than Cepheids, and much more common. Unlike Cepheids, their periods and luminosities don't vary much at all; their periods are all about 18 hours, and their luminosities are all about 100 times that of our Sun. There was just one of these stars (RR Lyrae itself) close enough to be measured precisely by Hipparcos, but another 20 stars of a very similar nature which Hipparcos could also measure. There are several other methods to estimate the distances to some of these stars, and some of them agree with each other at the 10 percent level.
RR Lyrae stars are bright enough that we can see them easily in the Magellanic Clouds, and in a few other members of the Local Group. But we can't measure them very well in the Andromeda Galaxy, or in any galaxy beyond the Local Group.
Main sequence fitting, as described in the previous lecture , compares the color-magnitude diagram of stars in clusters. The good news is that we can see plenty of clusters in the LMC; the bad news is that the stars in them have a somewhat different chemical composition than stars in the Milky Way.
We have found a few special eclipsing binary stars in the LMC. By combining measurements of their light, as the stars eclipse each other, with measurements of their radial velocities, as they move in their orbits, we can calculate the distance to such systems. It is necessary to use theoretical models of stellar atmospheres in the process, however, which lends some significant uncertainty to the resulting distance.
The amount of dust between us and a binary star can affect the calculated distance. Two sets of astronomers have used the same eclipsing binary (HV 2274) to measure the distance to the LMC -- and get results which differ by about 8 percent!
Tip of the Red Giant Branch (TRGB) Stars at a certain point in their lives evolve in the color-magnitude diagram to a particular point, which appears to have roughly the same luminosity for almost all stars. Many of these stars are close enough for Hipparcos to measure their distance.
The red clump is made up of stars in another point in their evolution. Just as stars which burn hydrogen into helium in their core tend to fall in one area of the color-magnitude diagram (the main sequence), so stars which are burning helium into carbon in their core tend to fall into another area, which we call the red clump. There is currently a heated debate raging in the astronomical community: are all red-clump stars the same, or do their properties vary from one galaxy to another?
Miras are very large, very cool, stars which pulsate slowly, over periods of hundreds of days. They can vary by up to a factor of 100 in brightness as they grow and shrink. There are some indications that Miras, like Cepheids, obey a sort of period-luminosity relationship.
Supernova 1987A was a giant stellar explosion that we saw in 1987. It has left a beautiful (but mysterious) set of rings:

Astronomers watched as the material in the rings was lit up by radiation from the supernova, in the first few months after it exploded. It was possible to estimate the absolute diameter of the ring, in kilometers, based on the speed of light and some spectral measurements. Knowing the absolute diameter (in kilometers), and measuring the angular diameter (in degrees), we can use trigonometry to figure out the distance to the supernova .. and, therefore, the distance to the LMC.
However, different astronomers have used different models for the geometry of the rings to end up with very different distances, and it's not clear who (if anyone) is correct.

Here's a table showing some recent results for the distance to the LMC, using these methods:


  method                    distance to LMC     
---------------------------------------------------------
RR Lyrae                      45 kpc  +/-  7  kpc
                              46           4
			      51          10       double-mode (Kovacs 2000)

main-sequence fitting         52      +/-  3

eclipsing binary stars        48      +/-  3       HV 2274 (Nelson et al 2000)
                              44      +/-  6       HV 2274 (Udalski et al 1998)
                              41      +/- 13       a different system

tip of red giant branch       52      +/-  5
                              51           6       DENIS (Cioni et al. 2000)

red clump                     44      +/-  6
                              52      +/-  5        

Mira variables                50      +/-  9

SN 1987A                      52      +/-  4 
                           <= 47      +/-  2

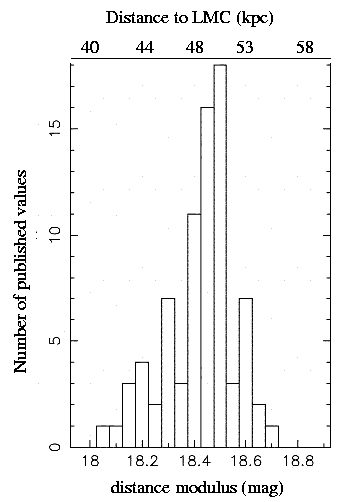
It seems clear that the distance to the LMC is somewhere between 40 and 55 kiloparsecs -- but there's still quite a range of possible values. There's currently quite a debate between those who favor the "short" distance (about 44 kpc) and those who prefer the "long" distance (about 51 kpc).

Since we use the distance to the LMC to set the zero-point for Cepheid variables, the distances to all other galaxies are linked to that of the LMC. The current uncertainty in the distance to the LMC means that distances to all other galaxies are also uncertain, by about 10 percent or more.

For more information, see

Sky and Telescope's Top 12 Naked Eye Variable Stars
MACHO project's interactive Cepheid Light Curve diagram
STScI page on SN 1987A
Phil Plait's page on SN 1987A
Calibration of the Extragalactic Distance Scale , a technical paper by Barry Madore and Wendy Freedman of the Key Project team.
A paper which derives distance to LMC using eclipsing binary stars
Patrick R. Durrell's description of the Tip of the Red Giant Branch (TRGB) method