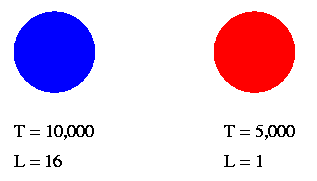
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Hipparcos measurements provide accurate measurements of distance for stars which are within about 100 to 200 parsecs. That includes a lot of stars, but is only a small fraction of the size of our galaxy. How can we extend these results for nearby stars to objects halfway across our Milky Way Galaxy, or to stars in other galaxies?
Part one of the answer is to use the inverse square law to calculate the distance to an object, given its apparent brightness -- which is easy to measure -- and its intrinsic luminosity. But how to we know a star's intrinsic luminosity?
Well, we can start by making some very simple (and wrong) assumptions, and then try to improve those assumptions.
Stars behave like all light-emitting bodies: their apparent brightness decreases if one moves them farther away. In fact, there is a simple mathematical rule which describes the change in a star's apparent brightness as a function of its distance away from us:
2
apparent brightness at distance A [ distance B ]
--------------------------------- = [ ------------ ]
apparent brightness at distance B [ distance A ]
This is called the inverse square law,
because the ratio of brightnesses depends on the square
of the inverse of the ratio of distances.
For example, suppose a star is exactly 10 parsecs away from us. We can measure its brightness -- call it "B". Now, if an alien race moves the star so that is becomes 20 parsecs away from us, we will measure a brightness which is only one-fourth of "B".
Another way to write the inverse square law involves the luminosity of a star. Luminosity is the total amount of energy emitted by a star each second; it can be measured in Watts, just like a light bulb. The luminosity is an intrinsic property of a star -- it doesn't depend on the star's distance from us in any way. The apparent brightness of a star can be written as
luminosity of star
apparent brightness of star = ----------------------
4 * pi * (distance)^2
Once again, note how the apparent brightness depends on the square of the distance.
So, if we know the intrinsic luminosity of a star, and we can measure its apparent brightness, then we can calculate its distance.
But how can we determine a star's intrinsic luminosity?
Two factors control the luminosity of a star:
luminosity = (area) * (energy emitted per area)
2 4
= ( 4 pi R ) * ( sigma * T )
where
So, if two stars are the size size, but different temperatures, the hotter one is more luminous:
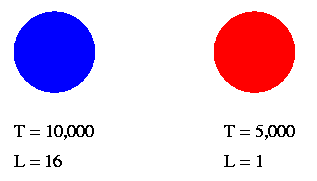
The difference grows very rapidly with temperature:
ratio of temperature ratio of luminosity
---------------------- ------------------------
1 1
1.1 1.5
1.5 5
2 16
3 81
10 10,000
If two stars are the same temperature, but different sizes, then the larger one is more luminous:
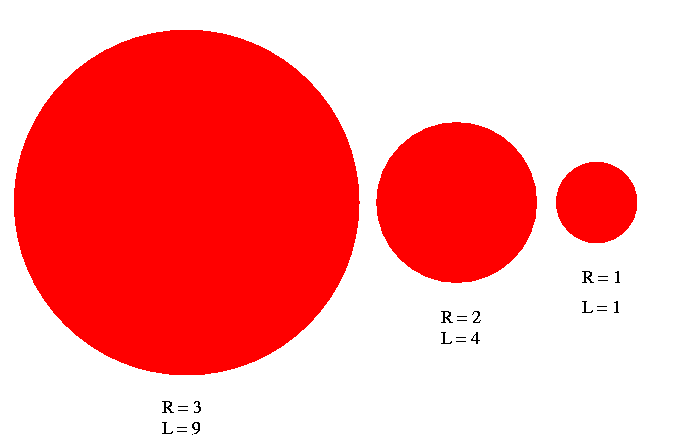
The difference grows more slowly with size:
ratio of radius ratio of luminosity
---------------------- ------------------------
1 1
1.1 1.2
1.5 2.3
2 4
3 9
10 100
The bottom line is that, unless we know both the temperature and the size of a star, we can't figure out its luminosity ... and that will prevent us from using its apparent brightness to figure out its distance. Rats.
We want to figure out the temperature and size of a star, so that we can determine its distance.
Temperature is actually pretty easy to determine:
The real problem is figuring out the size of a star. Hmmmm...
But, in an exception to the general rule, the universe turns out to be nice to astronomers (for once): there is a fundamental relationship between the temperature of a star and its size, which is true for about 90% of all stars. This relationship is revealed in the color-magnitude diagram, which is also called the Hertzsprung-Russell diagram.
Hipparcos measured the colors (and hence rough temperature) for lots of nearby stars. It also measured the distance to those stars, from which we can derive their luminosities. If we plot the luminosity versus the color, we find this:
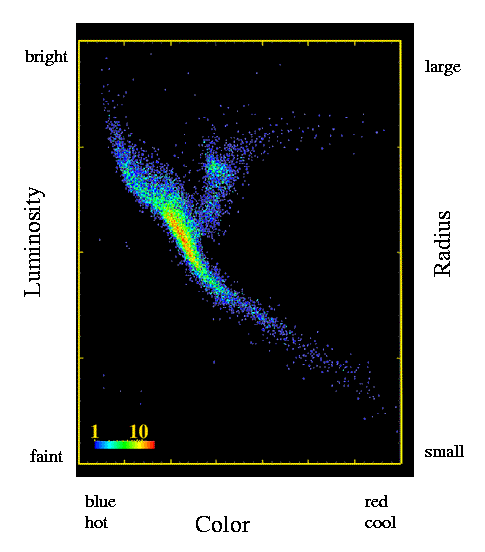
Rather than being scattered all over the graph, almost all the stars fall into a band which runs from upper-left to lower-right. This band is called the main sequence. Stars along this band
It turns out that the relatively simple relationship between temperature and size stems from the fact that all these stars are powered by the same fusion reactions in their cores.
Anyway, one important consequence is that we can almost use the color of a star (easy to measure) to guess its luminosity ... and that would give us its distance.
But -- there's one problem with this method: the giants.
A small fraction of stars (perhaps 5 percent) do not obey the ordinary relationship between color and size. These stars, called giants, are much, much larger than ordinary stars of the same temperature. Why? Because giant stars are not simply fusing hydrogen to helium in their cores; some have shells of fusing material surrounding an inert core, others are fusing helium into heavier elements. The differences in energy generation eventually (through a long chain of physical phenomena) cause the outer layers of these stars to move much farther away from the cores.
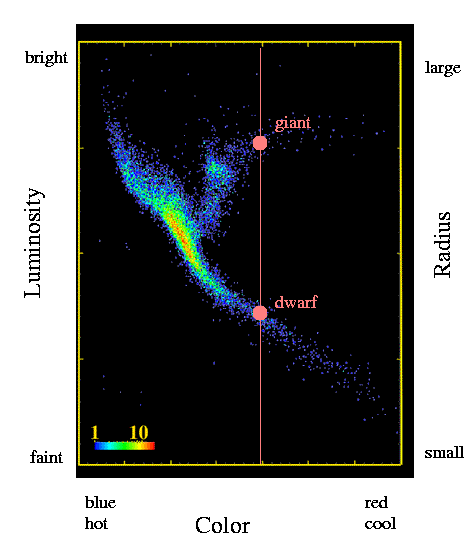
If we look at one particular star, and measure its color and apparent brightness, there are sometimes two possible values for its luminosity:
Now, most of the time, the star would turn out to be on the main sequence, so we could just always make that assumption. But even a small fraction of mis-classified stars with very wrong distances could screw up our whole view of the Galaxy.
Is there any way to separate the dwarfs from the giants, so that we can combine the apparent brightness of a star and its inferred luminosity to calculate its distance safely?
Yes! One solution is to concentrate on clusters of stars. There are several types of stellar clusters:
Open clusters contain mostly young stars, with lots of hot, blue stars:

Globular clusters have many more stars, most of which are relatively old, cool, and red:

The important thing about clusters is that all the stars in the cluster are at (nearly) the same distance from Earth. This means that if we make a color-magnitude diagram for stars which belong to a cluster, the difference between main-sequence stars and giants is easy to see:
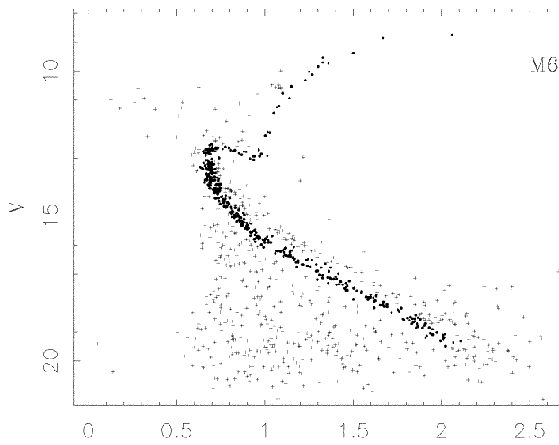
This diagram, for the open cluster called M67, shows that if we pick a star with color = 1, then
Suppose we look at another open cluster -- for example, the one called NGC 188:
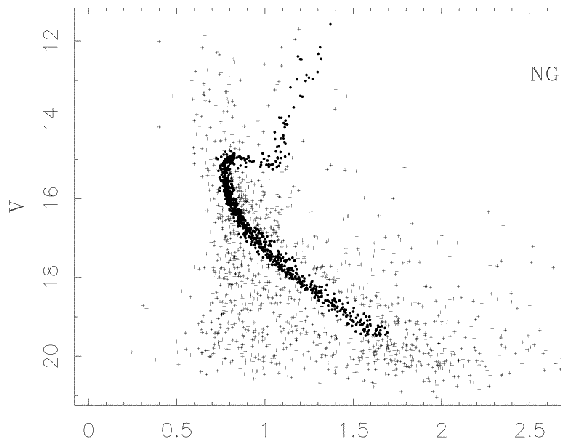
In this case, if we look at a star with color = 1, then
Great! Now, we can make a fair comparison of the distance between the two clusters, simply by matching up the stars on the main sequence with the same colors. It looks like we need to slide a star at color = 1 in NGC 188 upwards by about 1.5 magnitudes to make it match the brightness of a similar star in M67. That means that M67 is closer than NGC 188; and, using the inverse square law, we can figure out exactly how much closer.
So, simply by comparing the color-magnitude diagrams of two star clusters, we can figure out their relative distances from Earth. But how can we determine their absolute distances?
Simple -- thanks to Hipparcos. The Hipparcos satellite provided us with information with which we can make a color-magnitude diagram for stars with KNOWN distances. So, we just compare the color-magnitude diagram for a star cluster to the color-magnitude diagram from Hipparcos;
For more information, see
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.