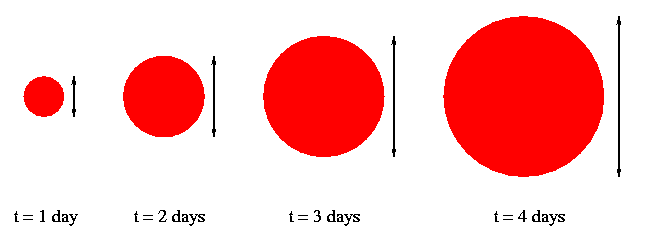Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
There are many different methods -- none of them very good -- which we can use to estimate the distance to far-away galaxies; or, more accurately, estimate the relative distances of a far-away galaxy and the LMC. All of our measurements of distant galaxies depend upon the distance to the LMC, which is used as a stepping-stone. So, if our distance to the LMC is uncertain by 10%, then every single distance to another galaxy will be uncertain by at least 10%.
Remember that, whatever we use to measure these vast distances, it must be very luminous. Otherwise, we won't be able to see it in very distant galaxies, halfway across the universe.
These methods fall into several different categories, but most of them make some assumptions about global properties of stars or galaxies (which are probably not true, on a case-by-case basis).
"Standard candles"
"Galaxies are built to the same plan"
"Basic physical principles"
Astronomers would like dearly to discover that there is some class of objects which all have exactly the same luminosity. We call such an ideal, mythical object a standard candle. If we knew
Unfortunately, we have yet to discover any truly standard "standard candle". Here are some of the candidates scientists have put forth over the years.
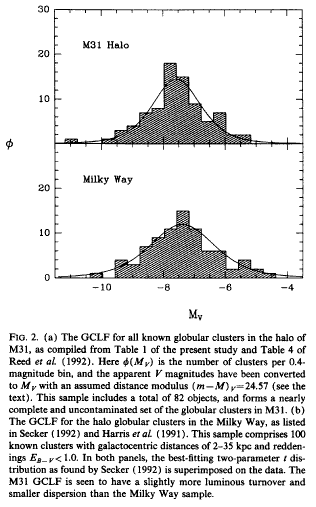
There are a few very bright clusters, a lot of "average" clusters, and a few very faint ones.
Now, if we look at other galaxies, we can see globular clusters around them, too:
We can make histograms showing the brightness of their globular clusters, too. For very nearby galaxies, like Andromeda, this works pretty well. The amount by which we need to shift the other galaxy's globular cluster histogram in brightness to make it match our Milky Way's tells us how far away it is (relative to the Milky Way).
But for really distant galaxies, we can only see the very bright globular clusters:
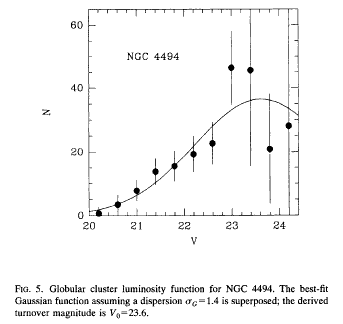
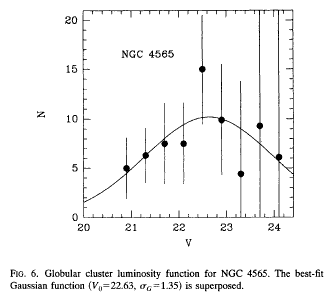
Trying to match these histograms against another galaxy's histogram is really hard: if we can see the "turnover" point (the "average" cluster), how can we match up the peaks to find the shift?
Overall, this method only works for relatively nearby galaxies: we can use it out at least as far as the Virgo Cluster (about 20 Mpc). I'm not sure that we can apply it out to the next big landmark, the Coma Cluster (at about 100 Mpc).
There are several mechanisms which can cause stars to explode. Type Ia supernovae occur when, in a binary star system, a main-sequence star dumps material onto a white dwarf companion:
If the white dwarf accumulates enough material to push its mass greater than about 1.4 solar masses, it explodes! It brightens over a period of about two weeks, by a factor of a million, and then fades slowly over several months:
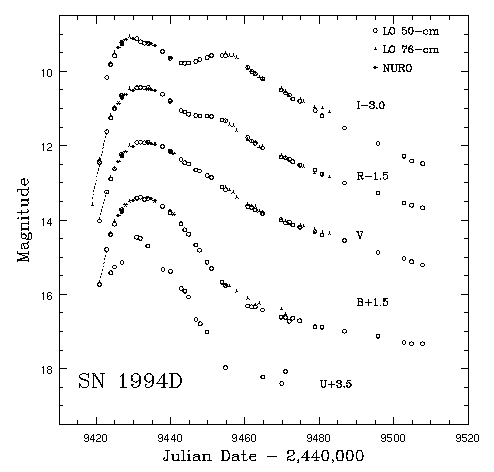
Since we think that all Type Ia supernovae occur when this limit of 1.4 solar masses is reached, we think that they all ought to have roughly similar peak luminosities. Do they? Look at this graph of peak luminosity (on the vertical axis) versus rate of decline after maximum (on horizontal axis, with slow decliners at left and quick decliners at right):
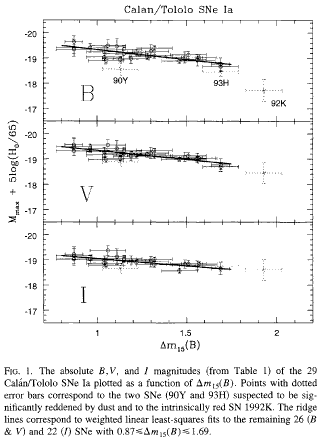
Clearly, some Type Ia supernovae are brighter than others, so they aren't standard candles. But it also appears that the difference in peak brightness is correlated with the rate at which they fade: slow faders are bright, quick faders are faint. There's hope that we can correct for the difference in peak luminosity by using the rate of fading after maximum ....
Type Ia supernovae are probably the closest thing to a standard-izable candle that astronomers have at the moment, and they can be seen at VERY large distances. Recent observations of very distant Type Ia supernovae have hinted that funny things are going on in the very distant universe ....
To be fair, there are indications that in many clusters, the very brightest members really are quite similar. For example, if all such galaxies really do have the same luminosity, then they should fall in a straight line in this diagram:
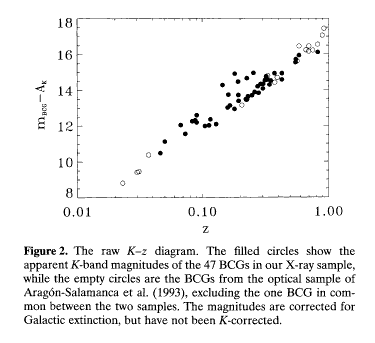
It appears that these galaxies are most similar if one looks in the near-infrared, possibly because the obscuring effects of any dust are minimized.
Overall, the BCG method is relatively imprecise (good to only about 10 or 15 percent, at best, with careful selection), but it can be used to very great distances.
Ordinary galaxies are certainly not all the same: there are big ones, small ones, spirals, ellipticals, bright and faint galaxies. So, it's obvious that they aren't standard candles. But perhaps there are some common features -- blueprints, one might say -- which underlie the structure of galaxies. If we understand these blueprints, we might be able to predict the luminosity of a galaxy from some other, more easily measured property.
But in distant galaxies, the stars all blur together to form what looks like a smooth bright area.
But if one looks very closely, one can see some "lumpiness" in pictures of distant galaxies. It's similar to the way that a smooth, nearly continuous reproduction of a photograph breaks up into "lumps" if one zooms in far enough:
The amount of lumpiness gives us a clue to the galaxy's distance:
By measuring the size of the surface brightness fluctuations, we can estimate the distance to a galaxy. This method does assume that the stellar populations in all galaxies (or maybe all elliptical galaxies) is very similar, and that most of the "lumpiness" is due to old stars near the peak of the red giant branch, and that the luminosity of those stars in the red giant branch is the same in different galaxies. That's a bunch of assumptions ... but it appears, empirically, that they are often satisfied.
The SBF method can be used out to about 60 Mpc from the ground (about twice as far as the Virgo cluster), and out to about 120 Mpc from space (about as far as the Coma cluster).
It turns out that the factor by which stars move faster in galaxy A is not simply "2"; instead, one can show with some basic calculations that it's closer to a factor of about sqrt(2), or 1.4. But, whatever the factor is (and, in real life, it's complicated by the range of sizes of spiral galaxies), it's clear that more stars should lead to faster motions.
A pair of astronomers named Tully and Fisher made a bunch of observations to check this idea: they measured
When the compared the luminosities to the orbital velocities, they found exactly the sort of relationship which the theory predicts:
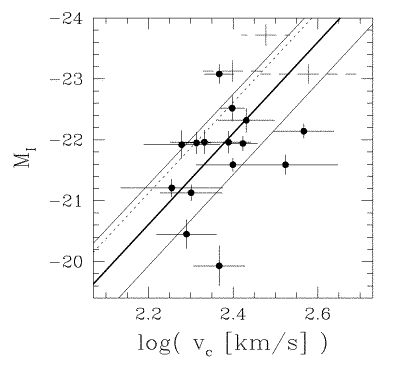
Now, the relationship isn't a very tight one: there's a lot of scatter. That means that the Tully-Fisher method is imprecise: it yields a distance to a single galaxy with an uncertainty of about 20 percent. On the other hand, spiral galaxies are common, so one might hope to average the distances to many spirals in a single cluster and find a precise distance to the cluster.
The two basic ideas underlying the methods described so far are:
Another approach is to study a single object, not a group, and apply basic physical principles to figure out its particular properties: size, mass, luminosity. This idea is attractive because it makes no assumptions about a whole group of objects. There are two techniques for measuring distances which follow this approach.
When the star runs out of fuel at its core, the core collapses on itself, then rebounds, sending a shock wave outwards. The shock wave
The outer envelope shoots outwards, making the star appear to grow larger in a linear way: twice as big after two days, three times as big after three days, etc.
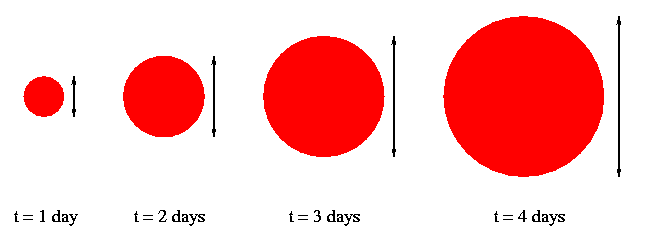
After just a few days, the temperature of the outer envelope cools down from 100,000 Kelvin to about 4,000 Kelvin, and then stays there for a few weeks. Why? Because as the outermost layers of gas cool past about 4,000 Kelvin, the hydrogen atoms go from an ionized to a neutral state -- and turn transparent. That allows us to see further into the layers of gas, to material which is a bit hotter, still about 4,000 Kelvin. Then those layers cool off a bit and turn transparent, so we see still deeper layers at 4,000 Kelvin, and so on.
The result of all this is that the star
radius of star = (expansion speed) * (time since explosion)
Now, if we know both the size and temperature of an object, we can calculate its luminosity from basic physical principles:
luminosity = (surface area) * (power per square meter)
2 4
= (4 pi radius ) * (sigma * T )
where sigma is the Stefan-Boltzmann constant.
So, by measuring the Doppler shift of lines in an expanding Type II supernova, and knowing something about its atmosphere, we can calculate its intrinsic luminosity. Comparing this to its apparent brightness, we can figure out its distance via the inverse square law.
How well does all this work? The theoretical uncertainty ranges from only 15 percent when we have many high-quality measurements of a supernova, to more than 40 percent if we have little data. Type II supernovae can be seen at great distances, but they fade away after just a few weeks, so it's difficult to get time on a big telescope quickly enough to follow the really distant ones.
We need to know
It's that last item -- the mass of the lens, and its distribution -- which is the real tough one. How do we know the mass of the lensing galaxy? Well, we need to assume that its properties are similar to those of other, nearby galaxies, which we can study in detail. So, this method really does depend, indirectly, on other methods for measuring distances to nearby galaxies.
How well does it work? There are very few gravitational lenses for which we know all the data needed to calculate distances. Steven T. Myers writes in "Scaling the universe: Gravitational lenses and the Hubble constant" that, as of early 1999, there were only about 4 systems available for use.
name uncertainty in distance
----------------------------------------------------
Q0957+561 20% (according to one group)
100% (according to another group)
B0218+357 20% mass model uncertain
PG1115+080 25% mass model uncertain
B1608+656 25%
Using gravitational lenses to measure distance is dangerous, because the results depend very strongly on the exact model of the mass distribution in the lensing galaxy. On the other hand, since we can see lensed quasars from extremely large distances -- they are probably the most distant objects we CAN see -- this method holds a great attraction for cosmologists.
method works out to accuracy comments
=======================================================================
Globular cluster 50 Mpc? 25% ? not entirely consistent
luminosity function with other methods
Type Ia supernovae > 3000 Mpc 8-10% must correct for the
decline rate effect
Brightest Cluster > 3000 Mpc 20-30% must select carefully
Galaxy
Surface Brightness 60 Mpc 5-8% (from ground)
Fluctuations 120 Mpc (from space)
Rotation vs. 1000 Mpc 20% relatively easy to do
Luminosity
Type II supernovae 200 Mpc 15-40% requires spectra of high
quality
gravitational lenses > 5000 Mpc > 25% ? works at huge distances,
but models of lens masses
very uncertain
For more information, see
Steven T. Myers' paper on using gravitational lenses to measure distances.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.