 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Astronomers have used gravitational lensing to attack three main problems:
Let's look at each in turn.
The Milky Way, like many spiral galaxies, appears to have a bright bulge, surrounded by a dimmer disk of stars. Most of the light from the galaxy as a whole comes from the bulge. If matter in our galaxy was distributed just like the light, then most of the mass would be concentrated near the center. In that case, stars and gas in orbit around the center of the Milky Way ought to have orbital speeds which depend upon their distance from the center: stars near the center should go fast, and those far from the center should go slow.
The situation would be similar to that in our Solar System, in which the Sun, at the very center, contains most of the mass. But instead, when we measure the orbital speed of stars and gas in the Milky Way, we find that the speed does not decrease with distance from the center. In fact, it remains relatively constant.
What's going on? One possible solution is that the Milky Way has a halo of material, which is distributed throughout the galaxy. If the halo material isn't very concentrated towards the bulge, then its gravitational pull on material in the outer reaches of the galaxy will keep its speed from dropping with distance from the center. But, this halo -- if its exists -- must be made up of dark matter, since we don't see light from many stars out there.
How to detect this dark matter? Use gravitational lensing! The Large Magellanic Cloud is outside our Milky Way, in the direction opposite the bulge. There aren't many stars in our galaxy visible in its direction -- but there might be lots of MACHOs (Massive Compact Halo Objects): very dim, cool stars, or old white dwarfs, or maybe sub-stellar objects, like very big planets.
In order to explain the orbital speed of material in the Milky Way, we believe that there must be about ten times as much dark matter in the halo as ordinary matter. Based on the number of stars we can see in our own galaxy, we can predict how many of them ought to lens stars in the LMC each year. The answer is -- about 1 per year. So,
What's the result? The MACHO project has seen about 3 events per year. That's significantly MORE than the number we'd predict for for the stars we can see ... but significantly LESS than the number needed to provide all the dark matter in the halo.
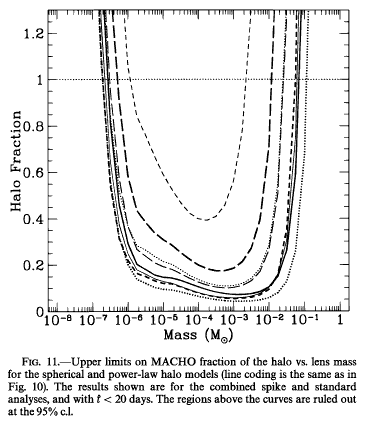
Does it rule out all kinds of dark matter in the halo? No! We can get some idea for the mass of each lensing object by measuring the length of time it brightens a background star. It turns out that, for lensing of stars in the LMC, the relationship between mass and length of lensing is
lensing time t = (130 days) * sqrt(M) M in solar masses
mass of lens lensing duration
(solar masses) (days)
=========================================
0.001 4
0.01 13
0.1 41
1.0 130
10 410
The microlensing search projects are most sensitive to events which last a few days to a few years. Here are the durations of the events seen towards the LMC so far:
34, 34, 42, 46, 62, 82, 87, 115, 138, 163, 267 days
What does this tell us? It tells us that in the halo of the Milky Way, there are very few, if any, objects with mass less than about 0.1 solar masses. That means that one can't make up the halo from lots of objects in the range of size between planets and small stars. The projects have ruled out a significant amount of mass in the form of objects between the size of Earth's Moon and the smallest stars.

In particular, brown dwarfs, which are objects not quite big enough to fuse hydrogen and shine as stars, and which have masses of 0.01 to 0.1 solar, are ruled out.
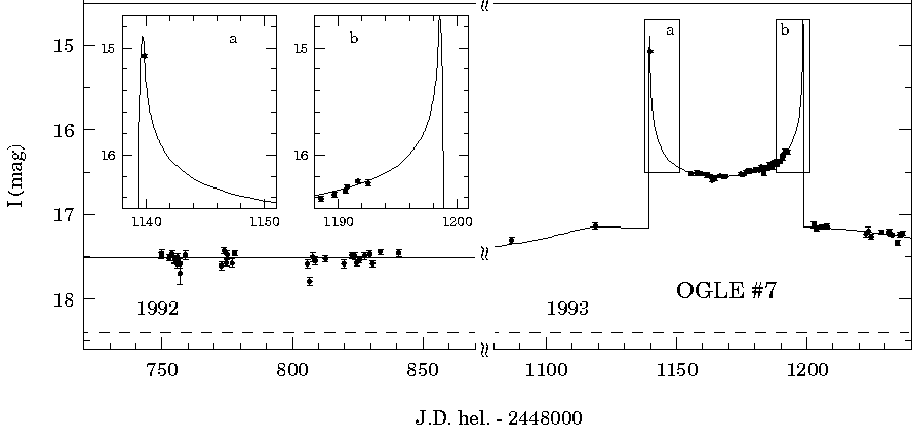
Note added Jan 16, 2001: Another year of work by the MACHO collaboration has added support to the idea that the microlensing events we see towards the LMC are, in fact, caused by material in the halo of the Milky Way. Some astronomers have pointed out that a star on the "near side" of the LMC can act as a lens for another star on the "far side" of the LMC. Thus, the microlensing events we see MIGHT have nothing to do with material in the halo of the Milky Way.
One way to test this hypothesis is to look very closely at the stars which are being lensed. If the lenses are in the Milky Way's halo, these background stars should be scattered randomly throughout the LMC. If the lenses are in the LMC itself, then the background stars should be mostly on the "far side" of the LMC. Recent observations of the lensed stars indicates that they are pretty well scattered throughout the LMC -- which lends support to the idea that the lenses are in the Milky Way's halo, rather than in the LMC itself.
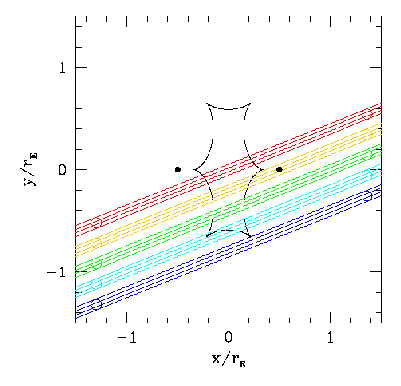
Funny things can happen when a background star passes behind a pair of lensing objects:
This follows the theory:
This "double-horned" light curve can vary a bit, depending on exactly how the background source moves behind the two lensing objects:
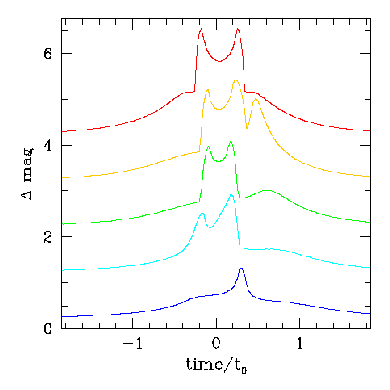
What if the lens consists of two objects, but instead of a star and another star, it's made up of a star and a planet going around it? If the background object passes
One group, called PLANET, is trying to do exactly that. They have a set of telescopes in the Southern Hemisphere
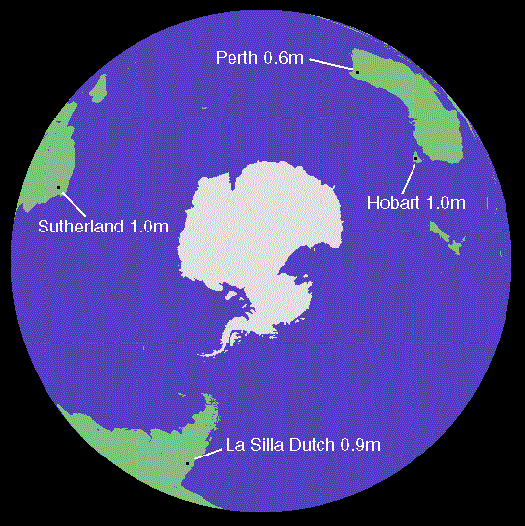
which allow them to watch a lensing event "around the clock" -- sometimes for more than 24 hours straight. They need to watch very carefully, because the gravitational lensing by a planet is much smaller in amplitude than that by its star, and it lasts for only a short time.
The PLANET team has seen a few abnormal events
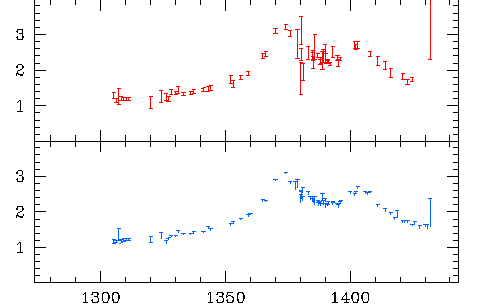
but all of them are due to binary stars -- not planets.
The MPS team measured very carefully the light curve of an event in 1997. They believe that we may have seen microlensing due to a planet orbiting a binary star system.
There are several methods astronomers can use to detect planets:
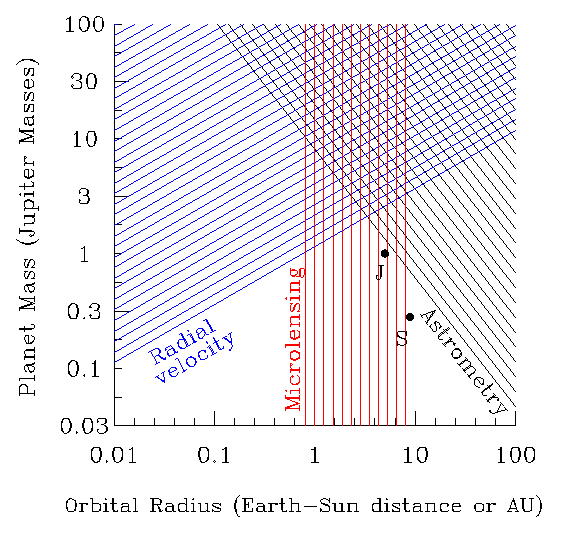
The bottom line on using gravitational lensing to detect planets around other stars: so far, after monitoring about 65 microlensing events, none has shown the effect of a planet of Jupiter's mass located a few AU from the star. The conclusion is that few -- less than 30 percent -- of stars monitored have planets like Jupiter at distances of 1 to 5 AU. Hmmm. This may mean that our own Solar System, which DOES have such a planet, may be unusual.
Astronomers are always trying to find new ways to measure distances to celestial objects. It turns out that, under the right circumstances, gravitational lenses may provide a method. Here's how it works:

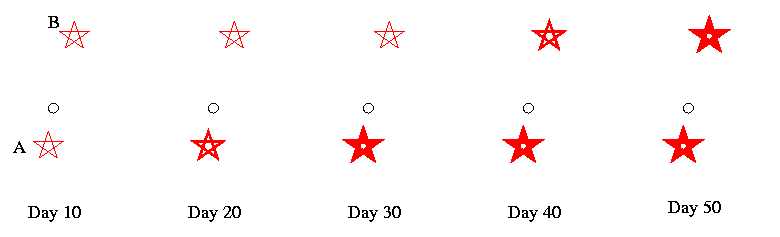
If a background quasar is not perfectly lined up with a lensing galaxy, we will see 2 (or 4) images which are not symmetrically arranged around the galaxy. Here's an example, the lensed quasar Q0957+561:
In such a case, the light rays travelling on one side of the lens must go farther than on the other side. That means that light from the background source must take a little longer to reach us in the direction of one image. There should be a time delay between the two images. If the background quasar suddenly increases its luminosity, then one of the two images should appear to brighten earlier than the other.
We can see the difference clearly if we plot the light curve of the two images, showing the brightness of each one as a function of time:
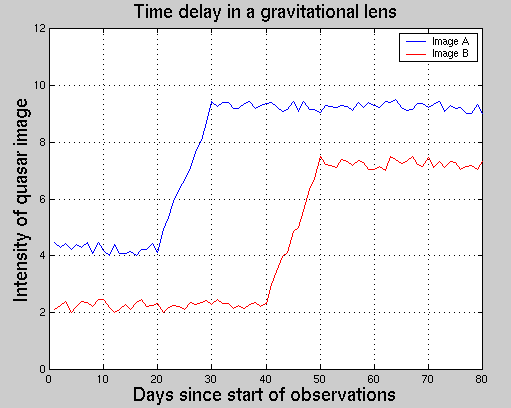
And the time delay can tell us something about the distance to the quasar (and the lens): all other things being equal, a big distance means a long time delay. If we can measure the time delay, then -- under the right circumstances -- we know the distance to the quasar!
The required circumstances are pretty tough to satisfy. We need to know:
It turns out that, after years and years of arguing over the time delay in the lensed quasar Q0597, astronomers had split into two camps: one claimed a time delay of about 540 days, and another about 415 days. In December, 1994, Ed Turner and a bunch of grad students at Princeton managed to acquire precise measurements of this quasar when image A suddenly dimmed:
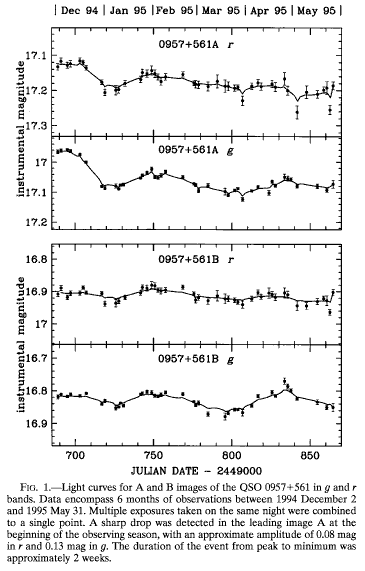
Aha! An opportunity to measure the time delay. If the true delay was the "short" version, about 415 days, then image B should show a corresponding dimming in February, 1996 -- 415 days later. But if the true delay was the "long" version, about 540 days, then image B should dim in June, 1996.
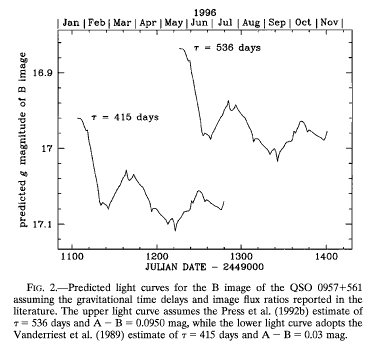
What happened?
A few months later, in February, 1996, image B really did fade a bit, just as the "short" delay predicted. And later observations showed that this delay of about 418 days was indeed the right one.
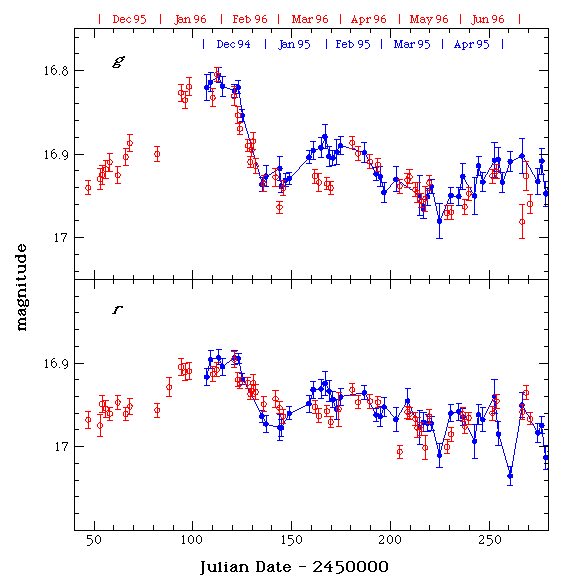
With the proper time delay, and a reasonable model for the mass of the lensing galaxy (this model is currently the most uncertain factor in the calculation), the distance to the quasar was measured to be about 1.6 Gigaparsecs. Wow.
For more information, see
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.