 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The URL for this experiment is
http://spiff.rit.edu/classes/phys236/moon_mount/moon_mount.html
Your job is the estimate the height of lunar mountains, based on the lengths of the shadows they cast. You'll need to acquire images of the moon, measure the apparent length of the shadows, look up some information (position of your features, altitude of the Sun at the time, etc.), and perform some calculations. Here's a step-by-step guide to the procedure:
Acquire image(s) of lunar mountains
If possible, we will go out to the Observatory and attach a video camera to the 16" telescope.
If we can't get images ourselves, we can use some taken on a previous night. You might try video images captured at the RIT Observatory on Feb 26, 1999.
Determine the selenographic location of mountains
You must determine the lunar latitude and longitude of the mountains or crater rims in your image. The videotape can help you to determine roughly where your image lies; use the Atlas of the Moon to measure the latitude and longitude of your mountain to the nearest degree. Use the convention that Eastern longitudes are positive, and Western longitudes are negative.
If you can find a name for your mountain or mountain range, record it. You may be able to look up more information about the feature in other lunar resources.
Measure apparent length of shadows
Click on the image of your crater, and save the image to the Desktop. Then go to the Desktop and double-click on the file icon for the image. That should start the Microsoft Photo Editor program, which will display the image. You can zoom in or out, pan across the image, and so forth. Look in the lower-left hand corner of the window to see the cursor coordinates, in units of pixels; they should change as you move the cursor across the image.
Measure the number of pixels from the peak of a mountain to the end of the shadow it casts. For a typical 640x480 image, you may find an apparent length of 10 to 40 pixels.
Pick several craters in the image with sharp, well-defined rims or walls. Measure and record the size of these craters in their longest dimension (which will probably be top-to-bottom).
Convert length from pixels to kilometers
Each pixel in the image is about 0.35 arcseconds; since there are 3600 arcseconds in a degree, this means that each pixel covers only a teeny-tiny fraction of a degree:
0.35 arcsec
1 pixel = --------------- = 0.000098 degrees
3600 arcsec/deg
Using the Voyager or SkyMap astronomical
programs, determine the distance D between the Earth
and the Moon at the time of the image.
You can then calculate the linear distance on the moon
covered by a single pixel:
1 pixel = D (km) * tan (0.000098 degrees)
Write down the size of a single pixel, in kilometers.
Use this formula to calculate the length of the shadow(s) in your picture, in units of kilometers.
Now check your result: look in your image to find a few craters with sharp, well-defined rims or walls. Look up the names of these craters in the Atlas of the Moon. The Atlas may provide a diameter for some of these craters. If it does, you can calculate a factor to convert from pixels to kilometers. Write down the conversion factor for as many craters as you can, and calculate the average.
You should find the conversion factor based on crater diameters is about the same as the conversion factor based on the angular size of a pixel. How closely does this conversion factor agree with the one you calculate above?
Determine the tilt of the lunar surface relative to the camera
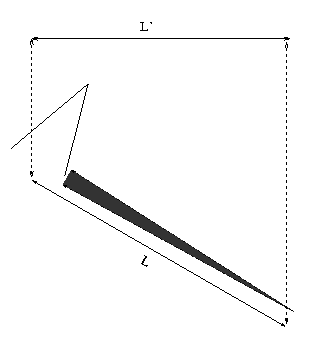
A picture of center of the lunar disk (near the lunar equator, halfway between the eastern and western limbs) has little or no distortion because the lunar surface is roughly face-on to the camera. But a picture of any other area will be tilted with respect to the camera; the closer the area is to the limb of the moon, the larger the tilt. This tilt causes foreshortening: it makes shadows appear to be shorter than they truly are. In the figure below, the true length L of the shadow appears to be shorter, L'.

You will need to correct for this foreshortening.
Use the lunar latitude and longitude of your mountain in the following formula:
1
tilt correction factor = ------------------------------
cos(latitude) * cos(longitude)
The correction factor is always larger than 1. Multiply your shadow length (in km) by this factor, and write down the corrected shadow length (also in km).
Sticklers for the truth will note that this correction factor
assumes that the observer is directly above the point
(latitude = 0, longitude = 0) on the lunar disk.
In truth, the sub-earth point is usually a few degrees away.
Those who wish to include this effect must look up the
selenographic latitude and longitude of the sub-earth
point, and then calculate
1
tilt correction factor = ---------------------------
cos(b - b') * cos(L - L')
where b and L are the mountain's selenographic coordinates,
and b' and L' are the sub-earth point's coordinates.
Determine the altitude of the sun over mountains
at the time of the image
You need to know the altitude of the Sun above the lunar horizon at the time of the photograph in order to determine the mountain's height from the length of its shadow. Go to the WWW site http://www.lunar-occultations.com/rlo/ephemeris.htm and enter the date and time of the observation. Our time zone is 4 hours behind UT during Daylight Savings time, and 5 hours otherwise; note that you may have to push the date forward one day. Then click on Calculate. Write down the following quantities:
Now you are ready to calculate the angle of the Sun above your mountain. Do it in two steps:
Step 1:
x = sin(Bo)*sin(latitude) + cos(Bo)*cos(latitude)*sin(Co + longitude)
Step 2:
angle theta = arcsin(x)
The angle theta is the elevation of the Sun above the horizon of the Moon, as seen from your feature, at the given time and date. Write down this angle. Check your answer: for any feature which casts long shadows, the angle should be between zero and fifteen degrees.
Calculate the height of the mountain
You are now ready to calculate the height of the lunar mountain. Consider the diagram below:

You know the length of the shadow, L, and the angle theta. You can calculate the height of the lunar peak with simple trigonometry. Write down the formula you need to use, and then plug in your values. What height do you derive?
Can you find another source which lists the height of your mountain, or other pictures of your mountain? Try using books in the RIT library, or the following WWW sites:
How does this height compare to the height of mountains here on Earth? Compare your lunar mountain to the tallest mountain in New York state, the tallest mountain in the USA, and the tallest mountain on Earth.
This page maintained by Michael Richmond. Last modified Mar 14, 2003.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.