Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
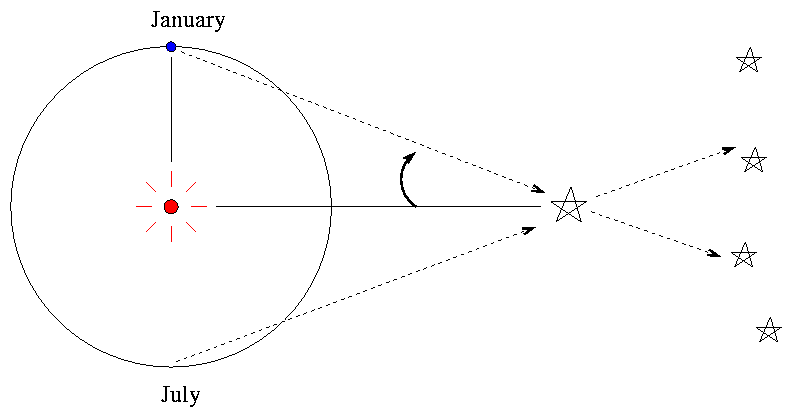
The simplest method for measuring distances to other stars -- and the most reliable -- is to look for a tiny shift in the apparent position of a star as the Earth moves around the Sun:
We can calculate the distance d from the parallax angle p with a little trigonometry:
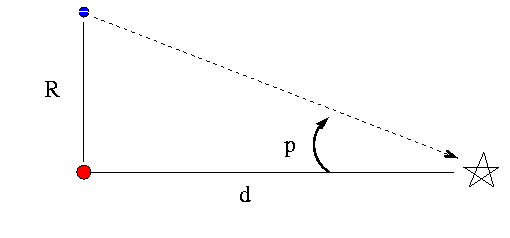
R
d = -----------
tan p
The distance R between the Earth and Sun, which is sometimes called "one Astronomical Unit", or "one AU" for short, is about 150 million kilometers.
So, all one has to do is to measure the shift in position of a star as the Earth moves around the Sun. Sounds easy, right? Well, it turns out that it isn't. In fact, it's really, really, really hard. The problem is that the shifts are tiny, because
Space is big. Really big. You just won't believe how vastly, hugely, mind-bogglingly big it is. I mean, you may think it's a long way down the road to the chemist, but that's just peanuts to space.
There is another problem, too. In order to measure the tiny shift in a star's position, one needs something against which to measure: a background. There are plenty of stars in the sky, of course, so one can use them as the background ... but they, too, will undergo small shift as the Earth moves around the Sun. One must somehow pick a star which is probably close to the Sun, and then find several stars near it in the sky which are probably much more distant; then the parallactic shifts of the background stars will be negligible. But how can one determine which stars are probably nearby, and which are probably distant?
Well, one can try two approaches:
In the eighteen-thirties, three astronomers followed these guidelines, each picking a different star which he guessed to be nearby.
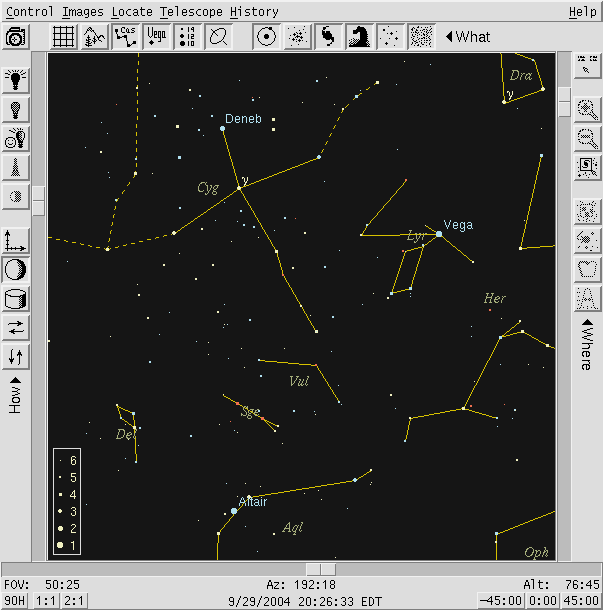
This chart of the summer sky shows two of these stars. Vega is obvious ... but do you know where 61 Cygni is?
It was a tight race. Henderson made his measurements in 1832, while working at the Cape of Good Hope in South Africa, but didn't reduce his data quickly. Bessel started observing 61 Cygni years later, but analyzed his results promptly. In 1838, he made (scientific) headlines by announcing that the parallax of 61 Cygni was 0.314 arcseconds. In the next few months, Henderson published a parallax of Alpha Centauri of about 0.75 arcseconds, and Struve a parallax of Vega of 0.1 arcseconds.
Q: Based on Bessel's measurement, how far away was 61 Cygni?
Express your answer in meters and in light-years.
1 light year = distance light travels in one year
1 arcsecond = 1/3600 degree
Since 1838, many astronomers spent decades measuring (or failing to measure) parallaxes to hundreds of other stars. Yes, just hundreds. It's a very tough business. The very best measurements of position one can make (from the ground) have an uncertainty of about 0.003 arcseconds, which means that only the nearest stars will show a significant shift.
In 1989, however, the European Space Agency launched a spacecraft called Hipparcos which was specially designed to measure very accurate parallaxes for tens of thousands of stars.
We can check to see how well Bessel did: go to the Hipparcos catalog search site and type into the "Hipparcos Identifier" box the ID for 61 Cygni: 104214. Then click on the "Retrieve" button. You'll see the record for Hipparcos' measurements of 61 Cygni A (one of the two stars in the binary system). The field labelled "H11" gives the parallax angle, in units of milli-arcseconds. Remember that Bessel published a value of 0.314 arcseconds.
You can find a table of distances to some nearby stars in the Appendix of your textbook.
You are going to see a bunch of words which may have astronomical meanings that don't quite match their ordinary, everyday meanings.
Once we know the distance to a star, we can determine its luminosity: the amount of energy it radiates each second. The Sun has a luminosity of about
26
solar luminosity = 4 x 10 Watts
When we look at stars in the night sky, they appear much, much fainter. But is that because they really do emit much less energy than the Sun -- or because they are just so far away that they appear faint?
Astronomers use a somewhat backwards system of measuring stellar brightness, called the magnitude system. You can find magnitudes described in section 2.1 of your textbook. Magnitudes grow larger as stars grow fainter, which seems strange. Magnitudes are also relative measurements: you can't really say much about the number of watts based on a magnitude. Instead, all you can do is determine the ratio of intensities of two stars from the difference in their magnitudes, using the formula
intensity (A) -0.4 * [ mag(A) - mag(B) ]
----------------- = 10
intensity (B)
Okay, fine. There are plenty of catalogs of stars which provide their magnitudes. Is there some way we can figure out how luminous these stars are, so that we can compare them to the Sun?
Yes, though it will take a couple of steps. Let's use Bessel's star, 61 Cygni A, as an example.
Step 1: The apparent magnitude of the Sun is about V = -26.5. The apparent magnitude of 61 Cygni A is (from the Hipparcos catalog) V = 5.2. Using the formula above, we can find the ratio of their apparent intensities:
intensity (61 Cygni A) -0.4 * [ 5.2 - (-26.5) ] ----------------------- = 10 intensity (Sun)
Wow. The Sun appears to be much, much brighter than 61 Cygni A. But you knew that already.
Step 2: The main reason 61 Cygni A seems so faint -- it is barely visible to the naked eye -- is that it is so far away. Is there some way we can calculate how much fainter it appears due to its great distance? Yes: we can use the inverse square law. It shows how the intensity of an object changes with distance:
2
intensity (when near) [ distance (when far) ]
---------------------- = [ --------------------- ]
intensity (when far) [ distance (when near) ]
So, let's imagine that we could move 61 Cygni A to the center of our Solar System, so it would be the same distance from us as the Sun. It would appear much, much brighter:
2
intensity (at Sun's dist) [ distance (when far) ]
------------------------- = [ --------------------- ]
intensity (actual dist) [ distance (when near) ]
Try to figure out whether 61 Cygni A would be as bright as the Sun, if we placed it at the center of the solar system. Does it have the same luminosity as the Sun?
Thanks to the Hipparcos satellite, we now know the distances to hundreds of thousands of stars which are relatively close to the Sun (within a few hundred light years). For each one of these stars, we can use its apparent magnitude and its distance to calculate its luminosity. Something quite surprising happens when we look at the luminosity and temperature of nearby stars ... but that's a story for the next lecture.
For more information
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.