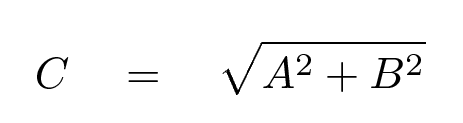
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
You will very often have the lengths of two sides of a right angle, and need to compute the length of the hypotenuse. At other times, you'll have the components of a vector, and need to compute the magnitude of the vector. The calculation itself is easy:
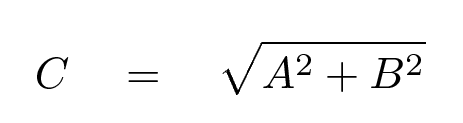
But how can you compute the uncertainty in this result?
The answer is ... slowly and carefully. You can use the same old rules you've seen before
Let's do an example, to see how it works. Suppose we have
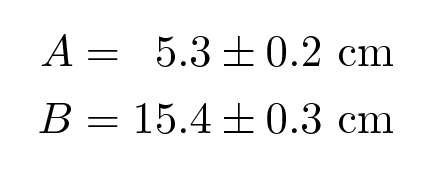
We'll use the notation ΔA to mean "the uncertainty in the quantity A". So we want to know
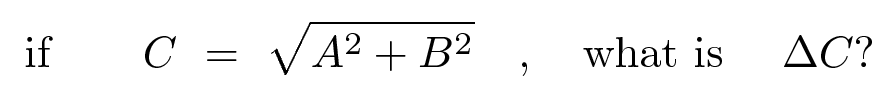
We can follow the simple rules, but it will take us three steps ...
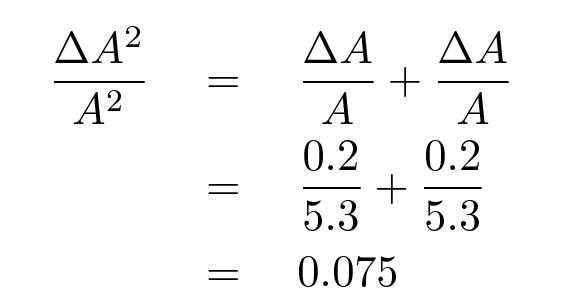
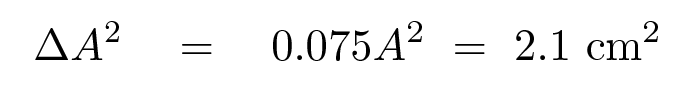
And end up with a value for A2 with its uncertainty:
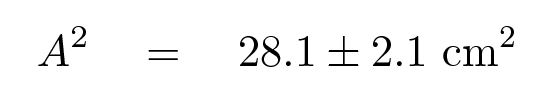
In exactly the same way, we can determine
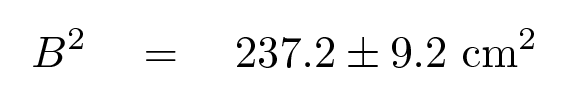
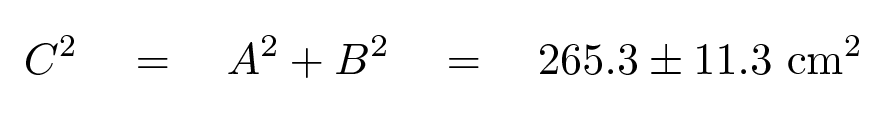
Now, the fractional uncertainty in C2 is around 4 percent:
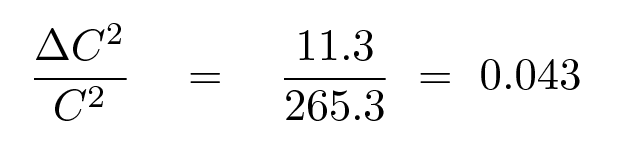
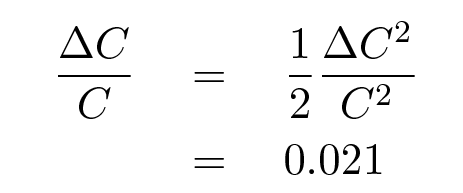
So we can now compute the uncertainty in the hypotenuse:
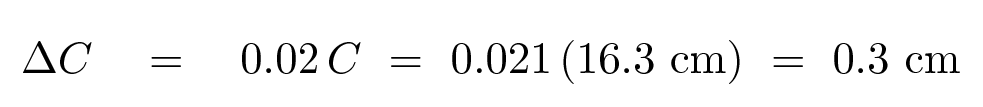
At last! After all that work, we can now write the value of the hypotenuse together with its proper uncertainty.
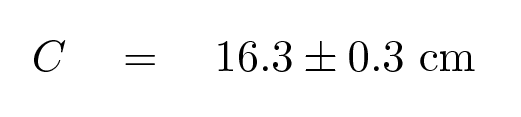
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.