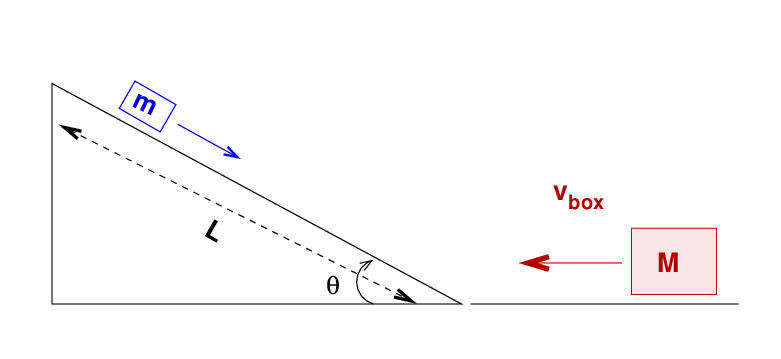
Practice problems for the second test

  1. A ramp of length L = 20 m is inclined at an angle θ = 20 degrees from the horizontal. A small block of mass m = 2 kg slides down the hill, with a coefficient of kinetic friction of μk = 0.1.

    1. What is the speed of the block at the bottom of the ramp?

    The block reaches the bottom of the ramp, where there is a frictionless level sliding area. At the same time, a big box of mass M = 5 kg comes sliding toward the ramp at vbox = 30 m/s. The small block and the big box collide elastically.

    1. What is the speed of the block after the collision?

    The block heads back up the ramp. Just as it reaches the top,

    1. What is the speed of the block at the top of the ramp?

    The answers (PDF)

  2. Astronaut Al (M = 80 kg) floats motionless in space. He holds a wrench (m = 2 kg) in his hand.

    At t = 0, Al throws the wrench at v = 3 m/s relative to his body, due East.

    1. Write an equation for the position of the wrench as a function of time.
    2. Write an equation for the position of Al as a function of time.
    3. Write an equation for the position of the center of mass as a function of time.

    "Ooops," thinks Al, "that was a mistake. I'm going to need that wrench to get back in the ship." At time t = 10 s, Al takes off his boot (mboot = 1 kg), turns, and throws it due West. Al's air supply will run out at t = 1000 s.

    1. In order to reach the wrench before he runs out of air, how fast must Al throw the boot away from himself?

    (Yes, this very large speed suggests that Al is in big trouble)

    The answers (PDF)

  3. A cone has height H and radius R. The cone sits on the ground with the pointy end up, like a traffic cone.

    1. If the cone is made of material with uniform density, how far above the ground is the center of mass?
    2. If the density of material depends on the height h above the ground, like so, 
                                                     h 
                  density(h)  =  K   * (1  +  --- )
                                               H
      where K is some constant, then how far above the ground is the center of mass?

    The answers (PDF)

  4. A hoop of radius R is oriented vertically. A strong is tied to point P, the very top of the hoop; the other end is tied at point Q, which is an angle θ away from the vertical. A bead can slide along this string without friction.

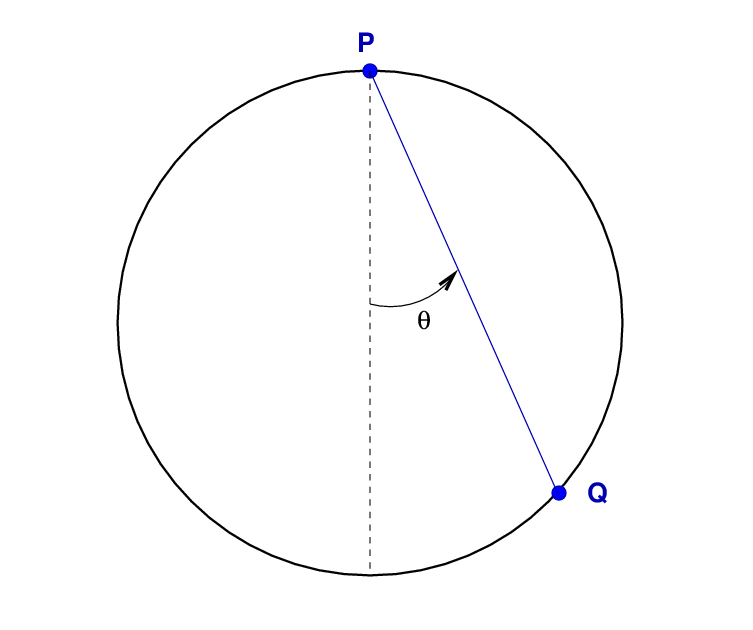
    1. The bead is placed at point P, then released from rest. How long does it take to slide to Q?
    2. What is its speed when it reaches point Q?
    3. Which choice of the angle θ will cause the bead to reach the far end of the string in the shortest time?

    The answers (PDF)