Dealing with vectors, Pirate-style

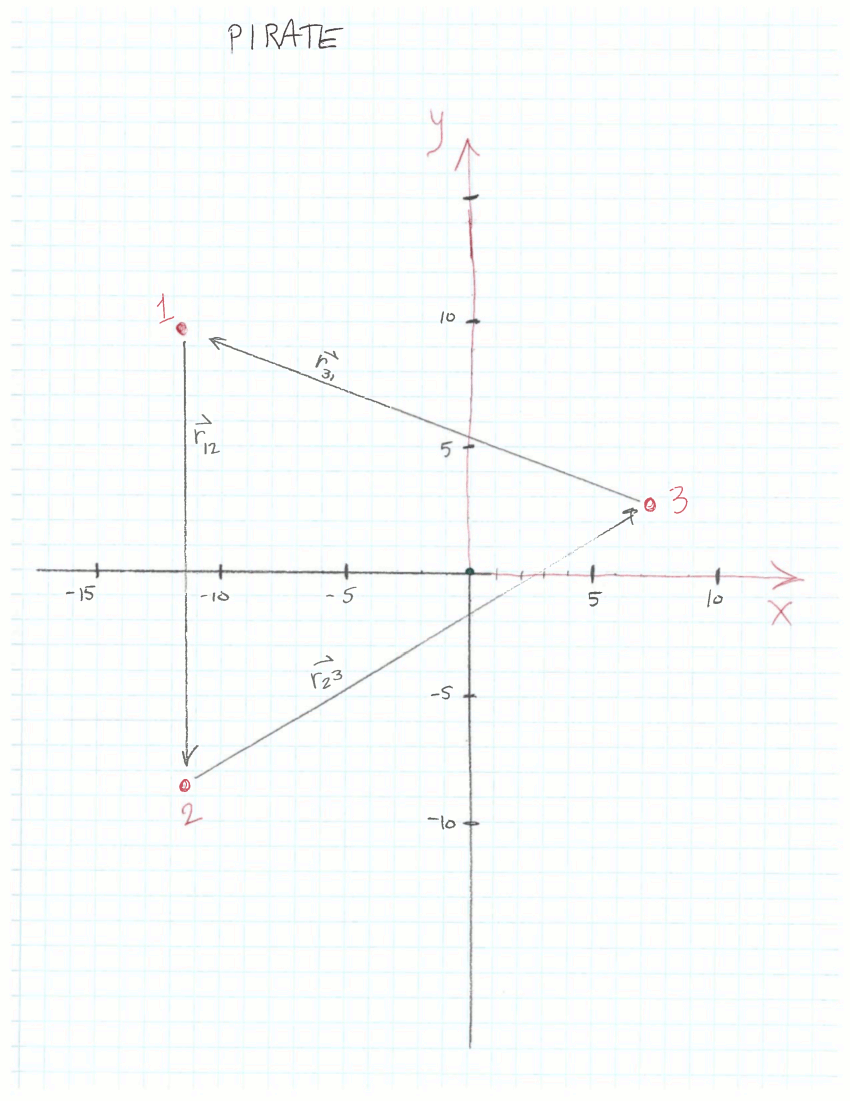
Once upon a time, on a deserted plot of ground, a crew of pirates found 3 colored dots. "This must be the map to buried treasure!" they cried, and carefully measured the positions of each dot.

                X (m)               Y (m)
----------------------------------------------------

 1          -11.8 +/- 0.3         9.7 +/- 0.2

 2          -11.4 +/- 0.2        -8.6 +/- 0.4

 3            7.1 +/- 0.3         2.8 +/- 0.3
----------------------------------------------------

The pirates erased all their coordinate markings and left.

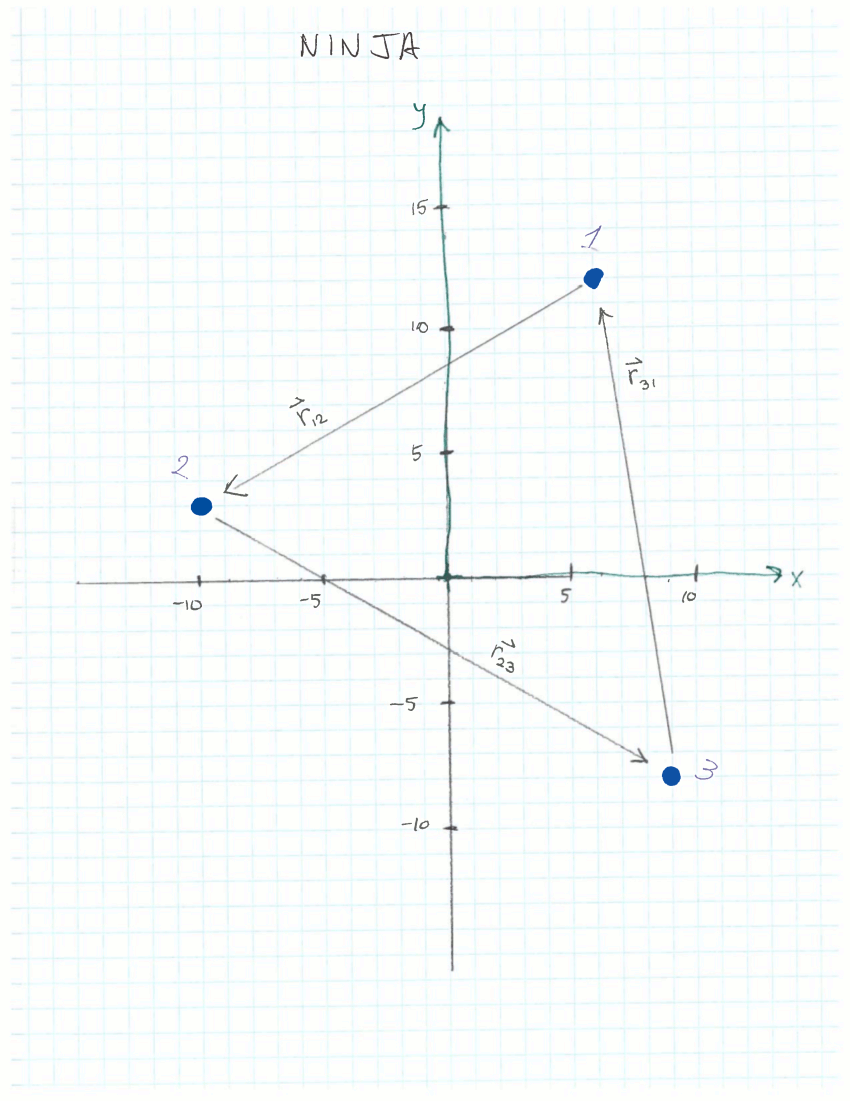
Several days later, a clan of ninjas stumbled across the same three colored dots. "Waah! Dots! Let us measure them!" The ninjas created their own coordinate system and made a careful set of measurements.

                X (m)               Y (m)
----------------------------------------------------

 1            6.0 +/- 0.2        12.0 +/- 0.3

 2          -10.1 +/- 0.4         2.9 +/- 0.2

 3            8.9 +/- 0.3        -8.1 +/- 0.3
----------------------------------------------------

Now, choose one team: Ninja or Pirate.

Use your team's measurements to compute the components of the vectors which run

• r₁₂ which runs from dot 1 to dot 2
• r₂₃ which runs from dot 2 to dot 3
• r₃₁ which runs from dot 3 to dot 1

For each component of each displacement, calculate the measurement uncertainty, using the error propagation rules. Fill in Table 1, below, for your team.

  Table 1:  Dot-to-dot displacement vectors 

                       Pirate                          Ninja

                X (cm)       Y (cm)              X (cm)        Y (cm)
--------------------------------------------------------------------------

 r12           +/-              +/-                +/-            +/- 

 r23           +/-              +/-                +/-            +/- 

 r31           +/-              +/-                +/-            +/- 
--------------------------------------------------------------------------

• Question 1: Compare the vector components (Table 1) you measured, against those of the other team. Are they the same or different, within uncertainty? Explain the result.

Now calculate the magnitude of the displacement vector between each pair of points and its uncertainty, using the information recorded above, and enter into Table 2, below. Compute the uncertainty in each magnitude as well.

How to calculate the uncertainty in magnitude? Well, consider a right triangle with sides A and B, and hypotenuse C. If you wish, you can read

• a detailed description of the uncertainty calculations
• a shorter version

But the end result is

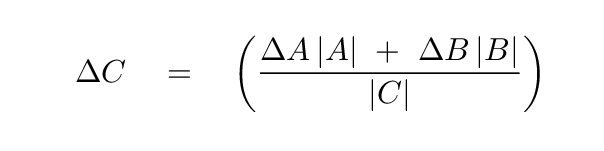
Now you can fill in the table below with the magnitude and uncertainty of each difference vector.

   Table 2:       Magnitude (cm) of the difference vectors

                        Pirates                     Ninjas 
-----------------------------------------------------------------

 r12                    +/-                          +/-

 r23                    +/-                          +/-

 r31                    +/-                          +/-
-----------------------------------------------------------------

• Question 2: Compare the vector magnitudes (Table 2) you measured, against those of the other team. Are they the same or different within uncertainty? Explain the result.

One last question; this one might require some thought. Suppose you now add your team's three displacement vectors from Table 1 together: r₁₂ + r₂₃ + r₃₁.

  Table 3:  Sum of the Dot-to-dot displacement vectors 

                       Pirate                          Ninja

                X (cm)       Y (cm)              X (cm)        Y (cm)
--------------------------------------------------------------------------

 r12           +/-              +/-                +/-            +/- 

 r23           +/-              +/-                +/-            +/- 

 r31           +/-              +/-                +/-            +/- 
==========================================================================

 Sum           +/-              +/-                +/-            +/-

--------------------------------------------------------------------------

• Question 3:
  • What should be the result of this vector sum?
  • Do your results agree with your expectation, within uncertainty?

In order to earn full credit for today's class, your group must submit to myCourses the following information (in a spreadsheet, or PDF, or plain text, or whatever):

1. names of all team members
2. copy of Table 1, with all numbers filled in
3. your answer to Question 1
4. copy of Table 2, with all numbers filled in
5. your answer to Question 2
6. copy of Table 3, with all numbers filled in
7. your answer to Question 3