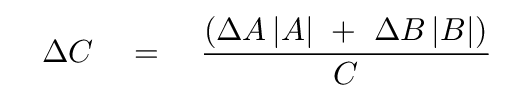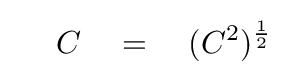
Pythagoras says that
C2 = [ A2 + B2 ]
The uncertainties in A2 and B2 are
( ΔA ) ( ΔB ) ( 2 * ------ ) * A2 ( 2 * ------ ) * B2 ( A ) ( B )
which means that the uncertainty in C2 must be the sum:
( ΔA ) ( ΔB )
Δ(C2) = ( 2 * ------ ) * A2 + ( 2 * ------ ) * B2
( A ) ( B )
which simplifies to
Δ(C2) = ( 2 * ΔA * A + 2 * ΔB * B )
Now we use the rule for propagating uncertainties when an expression is raised to the one-half power. Since the hypotenuse C is simply the square root of C2,
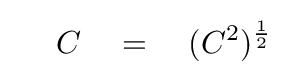
the rules say that the uncertainties in C and C2 are related like so:
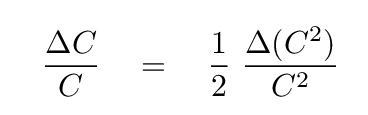
We can do a bit of algebra, and substitute our expression for the uncertainty in C2 from above,
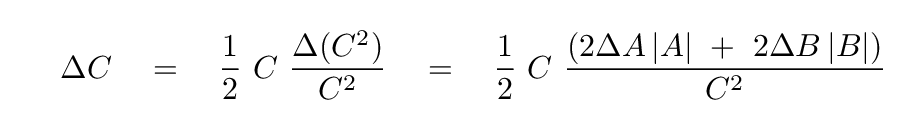
and the end result is not so complicated: