Predict the motion of a modified Atwood machine

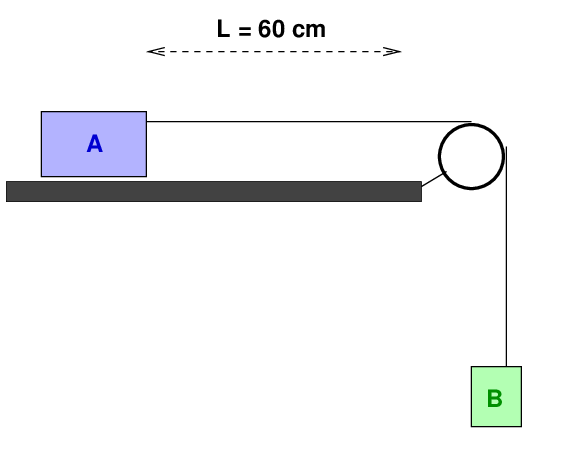
At the front of the room, I've set up a modified Atwood machine.

The quantities of interest are:

• mass of cart on track: A = 1524 g
• mass of hanging weight: B = 15 g
• length of the cart's motion: L = 60 cm
• local gravitational acceleration: g = 980 cm/sec²

Your job is to calculate two values:

1. the acceleration of the cart, a, in cm/sec²
2. the time, t, which is required for the cart to travel the distance L = 60 cm.

Okay, now that you've made your predictions, I'll run the experiment. All students -- those in classroom and those at home -- will help us to measure the time it takes for the cart to roll the distance L along the track. We'll run several trials, and I'll collect many measurements. Afterward, I'll compute the mean time t_μ and standard deviation σ. You must then use these values to answer the following questions.

3. Is your prediction equal to the measured time, within the uncertainty? In other words, does your prediction fall within the range (t_μ - σ) to (t_μ + σ)?
4. If not, what force(s) could account for the difference?

Bonus! Can you estimate -- quantitatively -- the size of the additional force(s) acting on the cart, in order to produce the observed acceleration?

• Perhaps these hints will help.

Copyright © Michael Richmond. This work is licensed under a Creative Commons License.