A modified Atwood's machine ... with friction

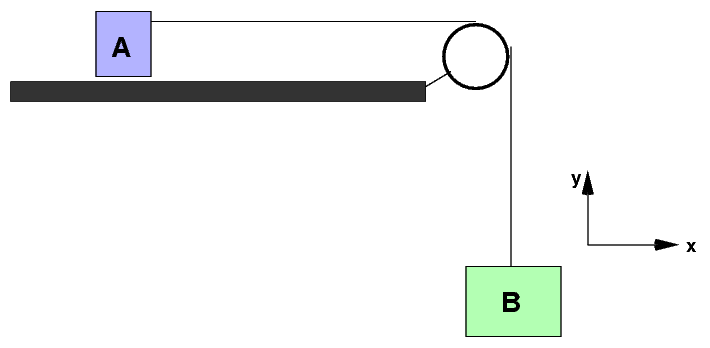
Consider the modified Atwood's machine:

Two masses (cart m_A, hanging block m_B) are connected by an ideal string passing over an ideal pulley, as shown. Note that an "ideal string" has the same tension force T everywhere along its length, but that force pulls

to the right, on the sliding cart m_A
up, on the hanging mass m_B

This time, let's include a friction force on the cart. Fill in the table at right with all the forces acting on the cart.


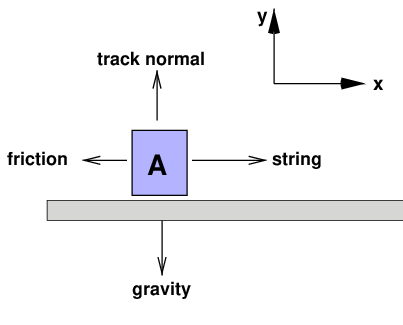
        force         x           y
       -------------------------------
        gravity       0         -mA * g

      track normal    0         +Fn
    
        string       +T           0

       friction      -Ff          0


       -------------------------------
        total      mA * ax     mA * ay = 0

Now, please write out expressions for the forces acting on the weight.


        force         x           y
       -------------------------------

        gravity       0        -mB * g
                                      
        string        0         +T 









       -------------------------------
       total   mB * ax = 0   -mB * ay

Finding the force of friction

We end up two equations, one for the cart and one for the weight. The key to solving them is to realize that the acceleration of the cart in x, a_x, is the same as the acceleration of the weight in y, a_y. We can simply replace them both with the single variable a.

This yields two equations with several unknowns. We can eliminate one unknown, the tension, by solving for it in the cart equation

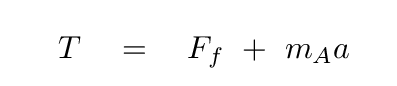
and substituting it into the weight equation

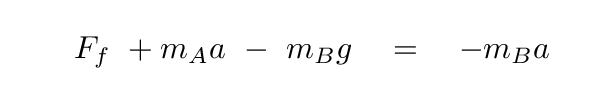
Now, in class, we MEASURED the acceleration of the cart, so we know its value. That means that we can solve for the force of friction.