 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
So we know that torque depends on two quantities:
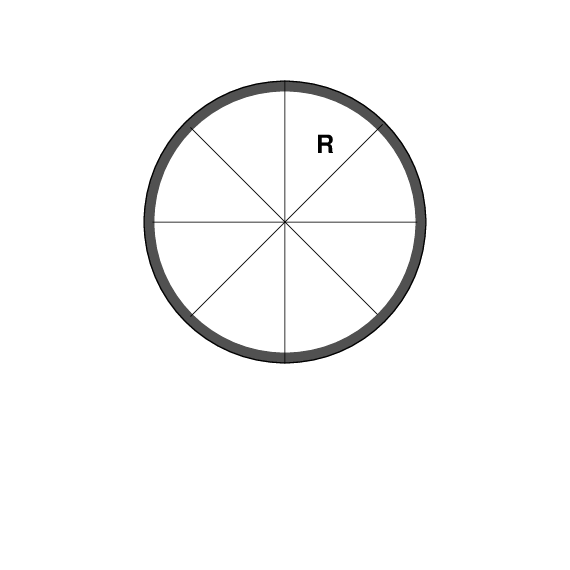
But it turns out that there's one more factor we must take into account: the DIRECTION of the force. Consider, for example, a bicycle wheel suspended in mid-air. The wheel has radius R and is motionless.

How dull. How boring. Zero angular velocity.
It would be much more interesting if the wheel were spinning, right? So, let's make it spin. We can change the wheel's angular velocity by applying a torque to it. That means pushing it at some distance from its rotational axis.
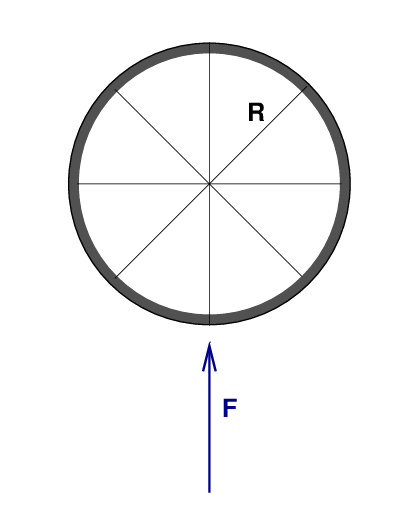
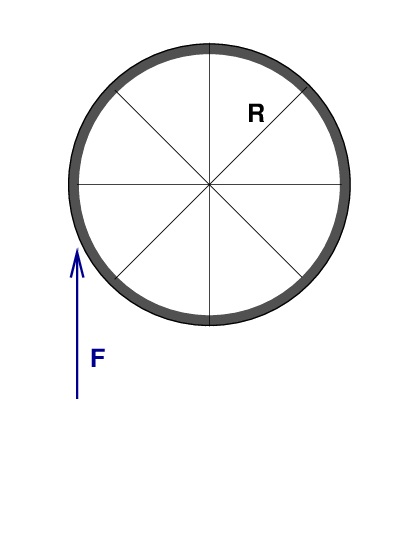
Q: What is the size of each force? Q: What is the distance of each force from the wheel's axis of rotation? Q: Will each force cause the wheel to start spinning equally?
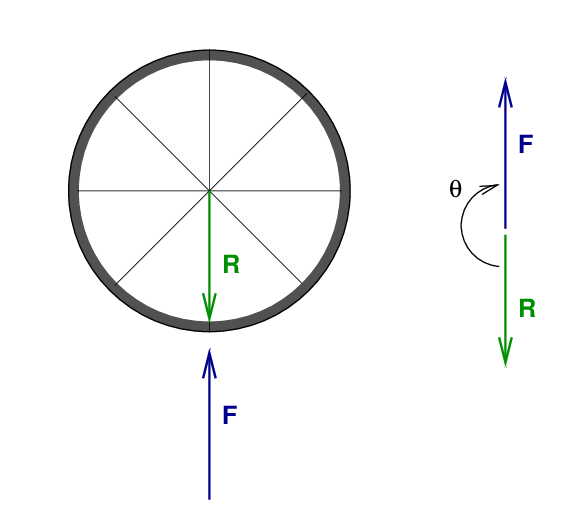
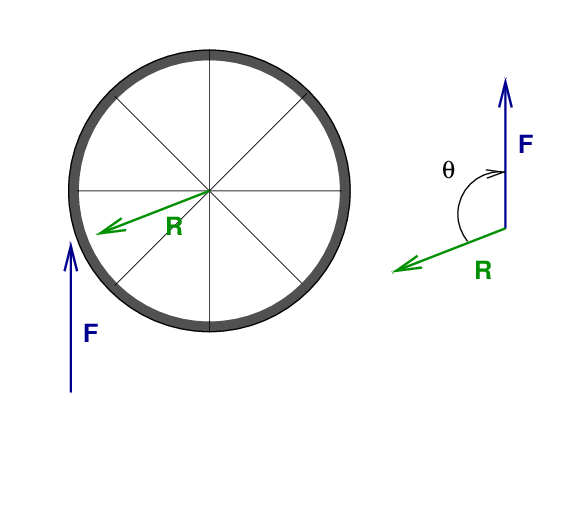
The torque created by a force depends not only on the MAGNITUDE of the force, but also on its DIRECTION relative to the radius vector. To find this direction, draw a copy of the force and radius vectors tail-to-tail.
Pushing straight up on the wheel from below means that the force vector is exactly θ = 180 degrees away from the radius vector. This won't produce any torque at all.
But pushing upwards on the side of the wheel WILL produce torque. In this case, the angle between force and radius is close to θ ≈ 100 degrees.
It turns out that the magnitude of a torque depends on the sine of the angle between radius and force vectors.
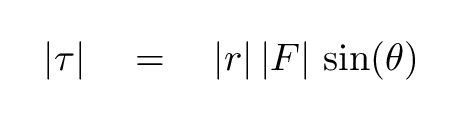
Now, torque is a vector quantity -- so which direction does it point?
The direction of the torque is perpendicular to both the force and the radius vector. In order to find it, you can use a second variety of the right-hand rule.
Let's practice.
In the movie Safety Last , Harold Lloyd finds himself hanging onto the minute hand of a clock for dear life.

If you look closely at the picture, you can see that the time is 2:42 PM.
Q: Estimate the torque on the minute hand, around the center of the
clock, exerted by Lloyd.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.