Adding waves with same amplitude, frequency, and wavelength

Suppose we have two waves with the same amplitude, frequency, and wavelength. The only difference between them is in their phase:

We can simplify things a bit by defining the phase difference between the two waves,

which leads to a slightly different way to write the equations of the waves

(yes, yes, strictly speaking, this means we may have to redefine the zeropoint of the time variable)

Depending on the value of the phase offset Φ, the two waves can reinforce each other or oppose each other. If Φ = 1 rad, for example, the superposition is somewhat larger than each individual wave.

In two special cases, the result is particularly simple:

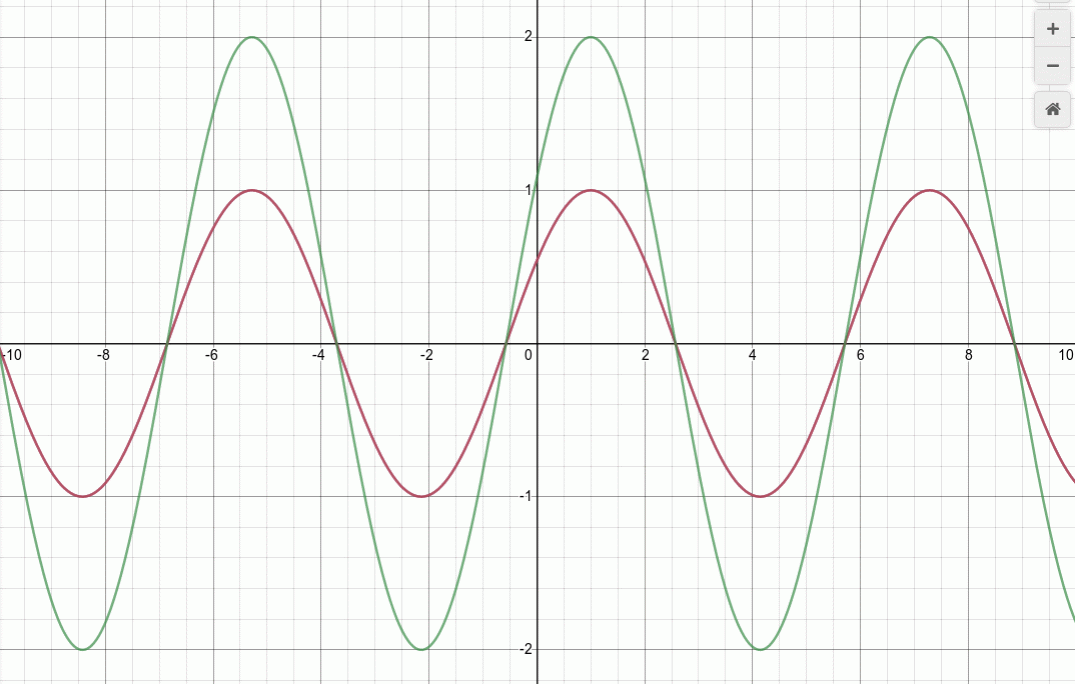
Φ = 0 means the two waves are completely IN PHASE, and so add completely constructively. The result is a superposition which is twice the amplitude of each input wave.

Φ = π means the two waves are completely OUT OF PHASE, and so add completely destructively. The result is a superposition which has no amplitide at all. (In the figure below, I've used Φ = 3.1 rad so that you can see the very small amplitude of the sum)

Okay, so the COMPLELELY constructive and destructive cases have simple results. But what about situations in which the phase difference lies between 0 and π radians? Is there any not-too-complicated way to express the sum of the two waves?

The answer is yes. But to find it, we'll need to go back to a trig identity. Do you remember this relationship from your days in pre-calculus courses?

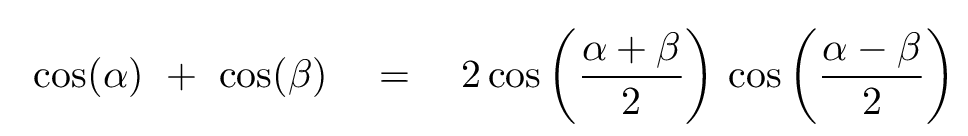
Let's try applying it to the addition of these two cosine functions:



   Q:  Can you use the trig identity to write the sum of the two
            cosine functions in a new way?

You should end up with

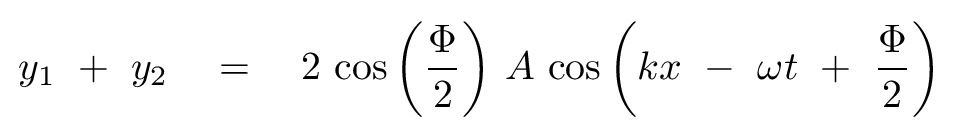
What does this mean? It means that when two waves with identical amplitudes and frequencies, but a phase offset Φ, meet and combine, the result is

a wave with the same frequency as the input waves ...
... but the phase of which is half of the original phase offset ...
... and the amplitude of which is 2 cos(Φ/2)

That's not so hard to remember.

The most important feature of this result is that the amplitude of the combined wave depends on the phase offset between the input waves. Depending on this offset, the result can be a wave with greater amplitude (constructive interference), or smaller amplitude (destructive interference) than the original waves.

Let's do an example:



    Q:  Two travelling waves meet:

          y1  =  (5 cm) * cos ( 3 rad/m * x  -  0.1 rad/s * t )

          y2  =  (5 cm) * cos ( 3 rad/m * x  -  0.1 rad/s * t  +  2 rad )


        Is the amplitude of the combined wave 

              a)  bigger than either original wave

              b)  smaller than either original wave

              c)  the same as either original wave


        What is the SPEED of this combined wave?

Examples of interference in the real world

Have you ever noticed the pretty colors which can appear in a thin film of oil?

Image courtesy of John and Wikimedia

Or in the scales on a butterfly's wing?

Image courtesy of Dystopian Optimist , licenced under Creative Commons

These are both created by the interference of light rays with thin films of material.

The basic idea is that if light encounters a thin film of material -- with a thickness d which is not too much larger than the wavelength of the light wave -- some of the incoming waves may reflect off the front boundary of the material ...

... while some of the waves may pass through into the film, but then bounce off the back surface ...

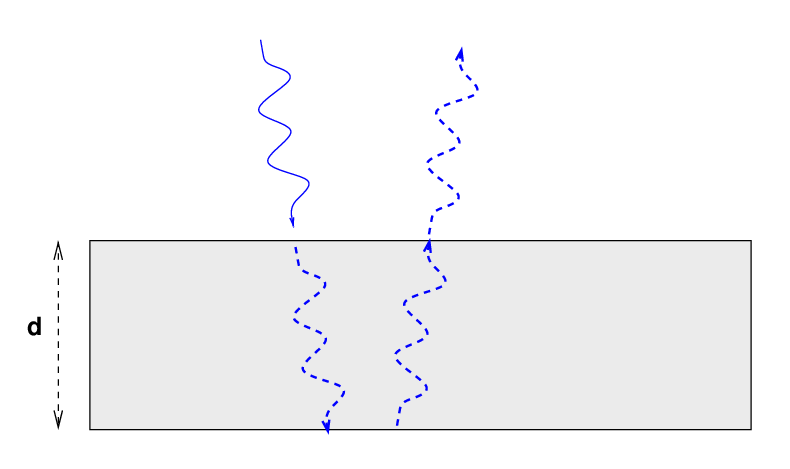
The result is that two sets of light waves head back from the film toward the original light source; and those two sources have travelled a different distance, leading to a phase difference between them.

(The waves can suffer from phase offsets due to their reflections from the front and/or back surfaces, too)

If the phase difference happens to be an INTEGER multiple of some particular wavelength, then the interference will lead to bright rays of light of that wavelength bouncing off; but if the phase difference is close to a HALF-INTEGER number of wavelengths, then very little light of that wavelength will bounce off.

Look again at the pretty colors in the oil slick:

Image courtesy of John and Wikimedia


 
  Q:  Can you explain why there are two arcs of green,
           two arcs of blue, two arcs of purple?

Some of you may be familiar with another real-world example of interference:

Image courtesy of bose.com

For more information

Thanks to Desmos for the nice pictures and interactive graphs!