Practice problems for final exam

  1. Earthquake! It sends waves travelling through the Earth's crust, which has a density of ρ = 3000 kg/m^3. The waves have a wavelength of λ = 430 m, a period of P = 0.8 s, and an amplitude of A = 2.1 m.
    1. Write an equation which describes the displacement of material as a function of position and time. Don't worry about the phase offset.
    2. What is the speed of the wave as it moves through the crust?
    3. What is the maximum speed with which little bits of the Earth's crust move as the wave passes?
    4. What is the intensity of this wave?

      5. Coal companies have marked out a region of the crust for a future mine. The region is a cube, 100 m on a side, still filled with rock; the company hasn't started excavating yet. The wave passes through this cube over the course of t = 6 seconds.

    5. How much energy does the wave deposit in the rock within this region?

    Read the answers (PDF)

  2. Joe stands inside his chemistry lab, which is a square room of length L = 15 m. He is x = 4 m from the west wall, and y = 10 m from the south wall. There is a fire alarm tucked into each corner of the room. The room is at 20 degrees Celsius, and at 1 atm of pressure.

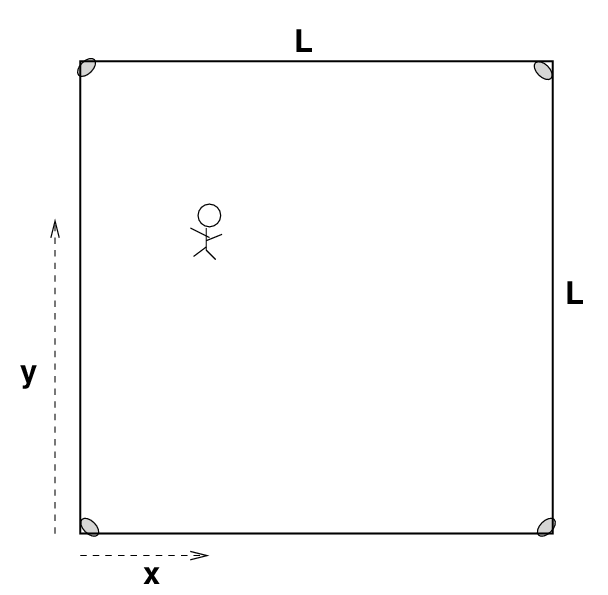
    Suddenly, the alarms begin to sound simultaneously: each buzzes with a frequency of f = 300 Hz and power P = 100 Watts.

    1. What is the intensity of the wave coming from each alarm when it reaches Joe?
    2. What is the amplitude of each wave, expressed in terms of over-pressure, when it reaches Joe?
    3. What is the net amplitude of the sound perceived by Joe, due to all the waves added together?

    Read the answers (PDF)

  3. Bob hangs a rope of length L = 100 m and mass m = 5 kg from a high beam. He adopts a coordinate system in which the height, y, is measured from the bottom of the rope. So y = 0 at the bottom and y = L at the top.

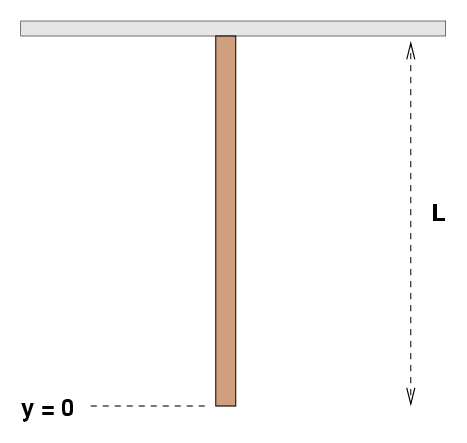
    Bob gets in a crane, rides up to the middle of the rope (y = 50 m), and whacks the rope with a stick. He watches as waves run away from the middle: one runs up to the top, the other runs down to the bottom. Which wave reaches the end of the rope first?

    To find out, follow these steps.

    1. Write an equation which yields the mass of the rope hanging below a point at height y.
    2. Write an equation which yields the tension in the rope at a height y.
    3. Write an equation which yields the speed of a wave in the rope at a height y.
    4. How long will it take the wave going up to reach the top of the rope? (Hint: it involves an integral of the velocity of the upward-going wave over time)
    5. How long will it take the wave going down to reach the bottom of the rope? (Hint: it involves an integral of the velocity of the downward-going wave over time)

    Read the answers (PDF)

  4. Little Justin wants to be a pop star, but every time he tries to hit an "A" (f = 440 Hz), his voice ends up producing the wrong note: f' = 450 Hz. "How can I fix my voice?" wonders Justin?

    As he wanders through the playground, he sees the big swingset. "Aha!" he thinks, "I'll just get in the swing and begin to go back and forth. If I hit the "A" while I am swinging backwards, the Doppler effect will lower my voice just enough to make the perfect frequency!"

    Justin climbs up onto the seat and begins swinging. He's careful not to exceed an angle of θ = 10 degrees, for fear of falling.

    It works! Justin's voice just barely hits the perfect "A" for a moment as he moves.

    1. Where is Justin in his swinging motion when this happens?
    2. How long is the rope of the swingset?
    3. How long is it between the moments when Justin's voice reaches the perfect pitch?

    Read the answers (PDF)