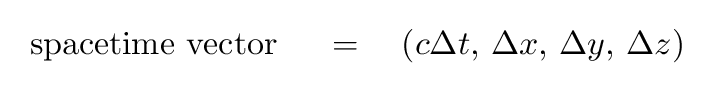
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Recall how we combined information about the interval between two events.
In general, observers in different inertial frames will NOT find the same values for t and for (x, y, z).
However, if we merge the variables into a single 4-dimensional quantity
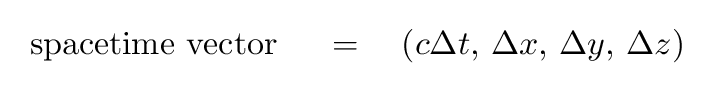
then it turns out that one particular combination of space and time will be invariant:
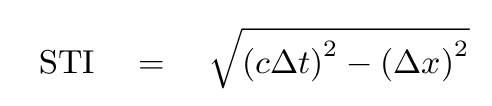
Q: What are the units of this interval,
as written above?
Q: Is it possible to convert this interval
into different units; for example,
can one express it in seconds?
If so, how?
This quantity, which has units of seconds, is also invariant.
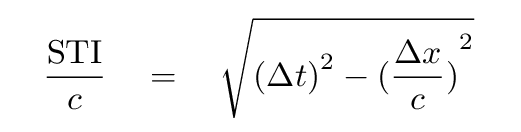
What does this quantity mean? We can compute its value, and we can assign it units, but what does it really represent?
Well, it has something to do with two events. Let's consider a special case: suppose that these two events are
According to Fred, these events occurred in exactly the same place. Therefore, the distance interval Δx between them is zero, and, according to Fred, the result simply represents the time between the two events. Because Fred was present at the location of the two events, his measurements yield the proper time between the events: that is the shortest interval of time between them that any inertial observer can measure.
Let's look at momentum and energy in the same way. In this case, we are considering just a single particle at a time, not two particles.
In general, observers in different inertial frames will NOT find the same values for E and for (px, py, pz).
However, if we merge the variables into a single 4-dimensional quantity
then it turns out that one particular combination of energy and momentum will be invariant:
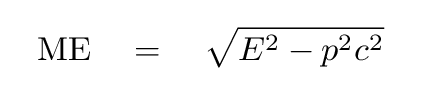
Q: What are the units of this interval,
as written above?
Q: Is it possible to convert this interval
into different units; for example,
can one express it in kg*m/s?
If so, how?
This quantity, which has units of momentum (kg*m/s), is also invariant.
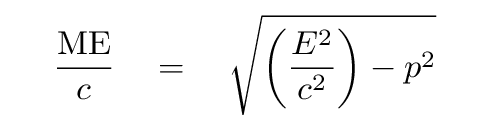
One can even compute a quantity which has units of kg, if one wishes.
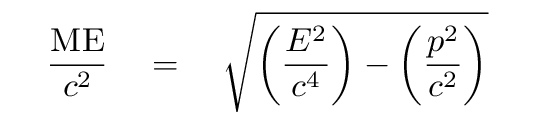
What does it mean? This expression has something to do with the properties of a single particle. In one special frame -- the frame in which the particle is at rest -- this quantity is equal to the energy of the particle, because, in that frame, the particle has no momentum (it's not moving). We could call this the rest energy of the particle. If we divide the invariant quantity ME by c^2, to convert it to units of kg, then we can call it the rest mass of the particle.
The Blue Man throws a ball (m = 0.2 kg ) at a speed of v = 0.5 c to the right.
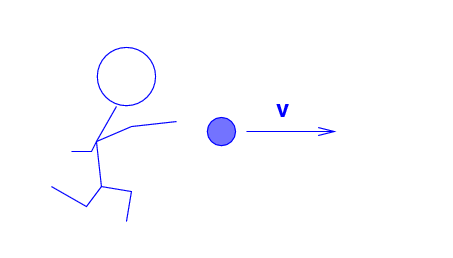
Q: What is the momentum of the ball,
according to the Blue Man?
What is the total energy of the ball,
according to the Blue Man?
What is the momentum-energy of the ball,
according to the Blue Man?
But the Blue Man and the ball are all travelling across the landscape at a speed of w = 0.8 c to the right, as measured by the Red Men.
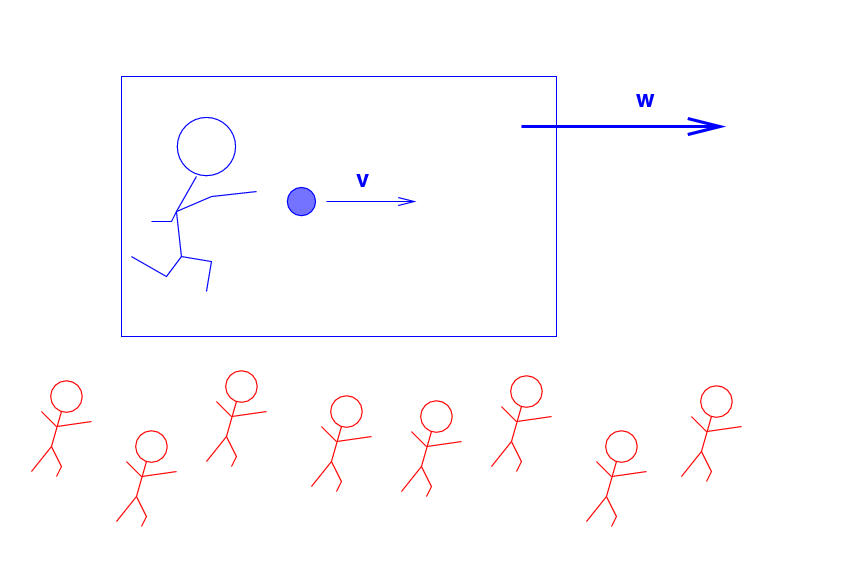
Q: What is the momentum of the ball,
as measured by the Red Men?
What is the total energy of the ball,
according to the Red Men?
What is the momentum-energy of the ball,
according to the Red Men?
The Green Man, inside a very small Green Room which fits completely inside the Blue Room, happens to be flying to the right at exactly 0.5 c relative to the Blue Man.
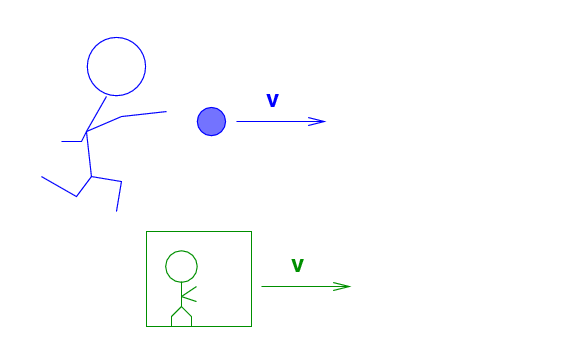
Q: What is the momentum of the ball,
as measured by the Green Man?
What is the total energy of the ball,
according to the Green Man?
What is the momentum-energy of the ball,
according to the Green Man?
If momentum-energy is a conserved quantity, why don't we use it in "normal" physics? Why didn't you learn it in high school?
Well, let's try using it, and see what happens.
Fred throws an ordinary ball of mass m = 0.2 kg to the right at v = 40 m/s.
Q: What is the momentum of the ball,
as measured by Fred? Try to use
the relativistic expression.
Multiply the momentum of the ball
by c to form the expression
p c. Write it down, too.
What is the total energy of the ball,
according to Fred? Try to use
the relativistic expression.
What is the momentum-energy of the ball,
according to Fred? Try to use the
relativistic expression.
As you can see, at ordinary, everyday speeds, the rest energy of an object is much, much, much larger than its kinetic energy, and also much, much, much larger than its (momentum times c). Two different low-speed observers will compute the same momentum-energy combination, but, for practical purposes, they will each end up with just the rest energy.
In ordinary life, mass, energy, and momentum do NOT interact strongly. That is why you probably learned three different conservation laws in high school physics:
In the relativistic realm, these three laws merge into a single rule, in which one particular combination of the elements of a 4-dimensional vector is invariant to all inertial observers.
Jane sits on Earth while her sister Sally flies away on a rocket at v = 0.9c. Jane sends a message to her sister, encoded in a laser beam. When Jane fires the laser, it produces photons with the usual reddish wavelength of lambda = 640 nm.
Q: What is the energy of each photon?
What is the momentum of each photon?
What is the momentum-energy of each photon?
Sister Sally collects the laser beam with her telescope and decodes the message. Of course, she doesn't measure the same wavelength as her sister -- she measures a much LONGER wavelength.
Q: What is the wavelength of each photon,
according to Sally? (hint)
What is the energy of each photon?
What is the momentum of each photon?
What is the momentum-energy of each photon?
Is the momentum-energy of a photon invariant, too?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.